目录
归并排序
1.基本思想:
2.原理图:
1)分解合并
2)数组比较和归并方法:
3.代码实现(递归方式):
归并排序的非递归方式
原理:
情况1:
情况2:
情况3:
非递归代码实现
归并排序的特性总结:
排序算法复杂度及稳定性分析
什么时稳定性?
各种常见排序算法的总结
归并排序
1.基本思想:
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,
该算法是采用分治法(Divide andConquer)的一个非常典型的应用。
将已有序的子序列合并,得到完全有序的序列;
即先使每个子序列有序,再使子序列段间有序。
若将两个有序表合并成一个有序表,称为二路归并。
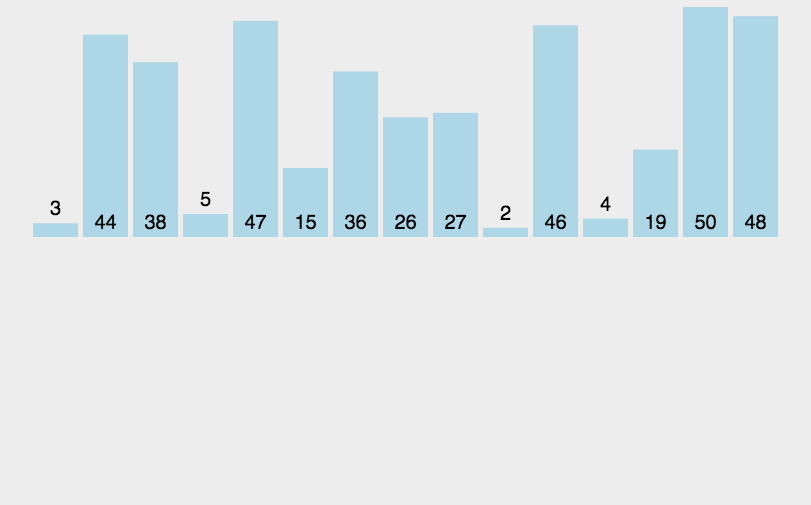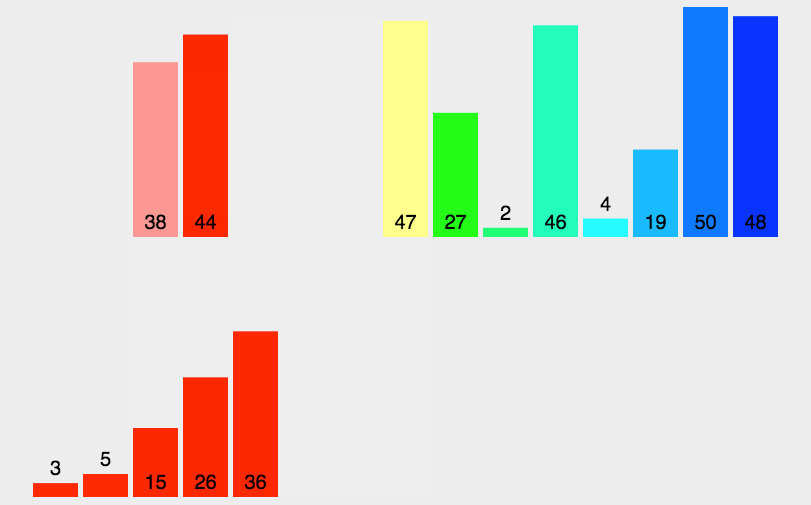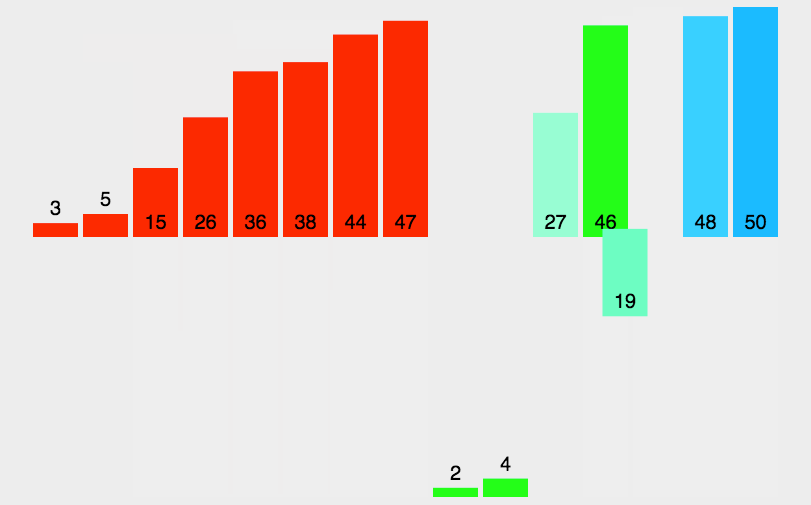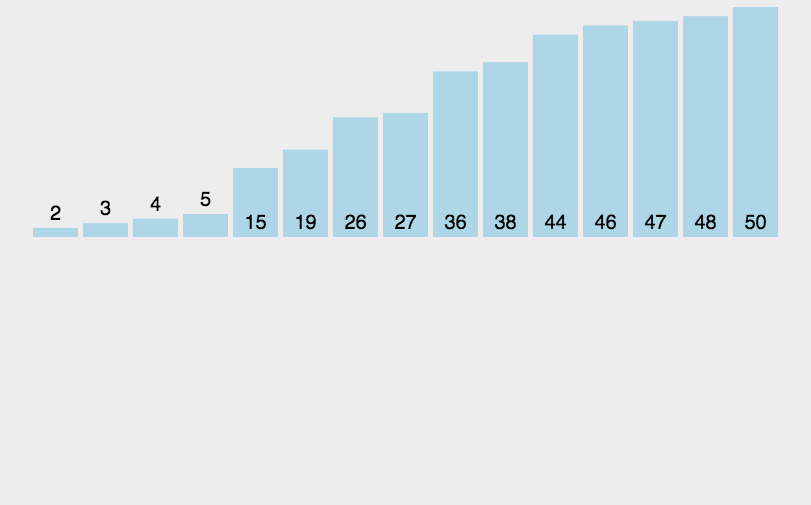
2.原理图:
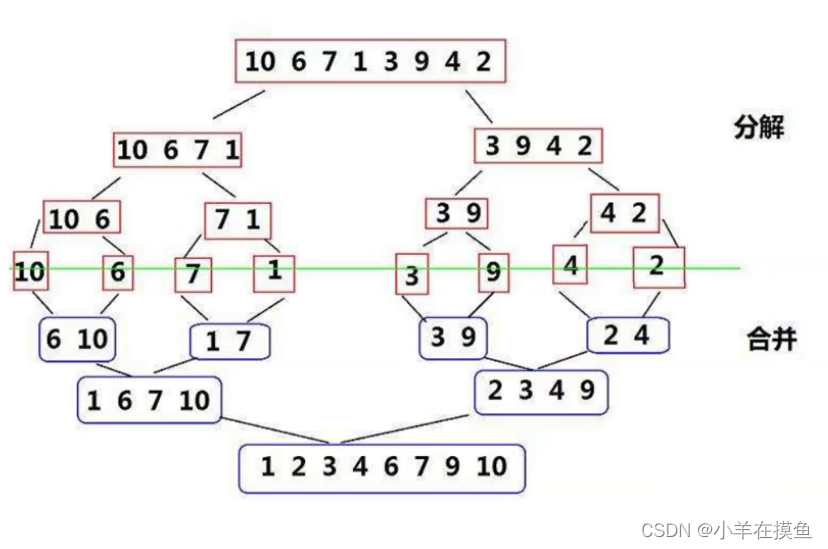
1)分解合并
第一层将一个数组分两个大组,
第二层再继续分,直到分成每组都只有一个为止
分解完了之后就是进行合并,每两个小数组,按顺序合并成一个大的数组
最终,合并称为一个有序的集合
动图效果:
归并排序是在原数组上进行的,用一个临时数组来做归并,把归并好的元素复制回原数组
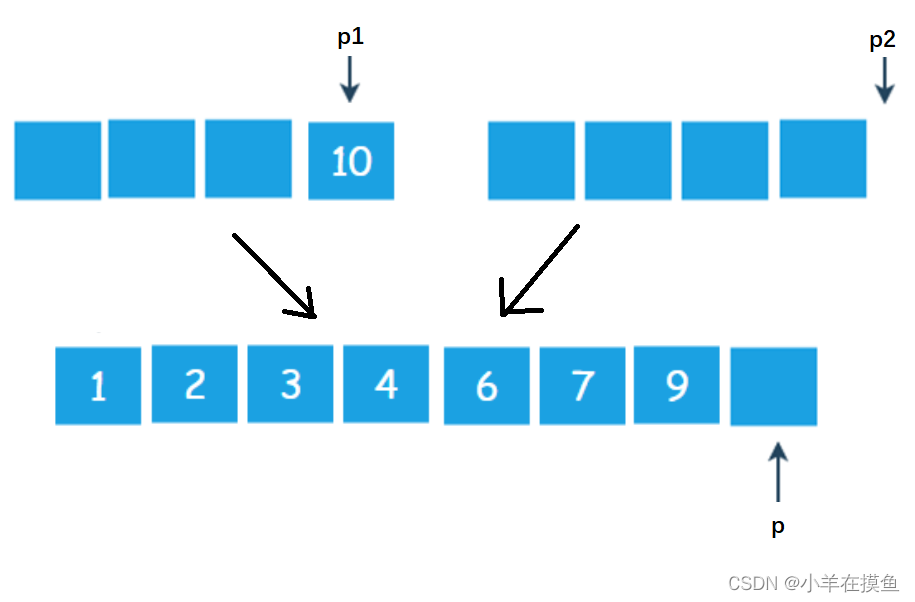
2)数组比较和归并方法:
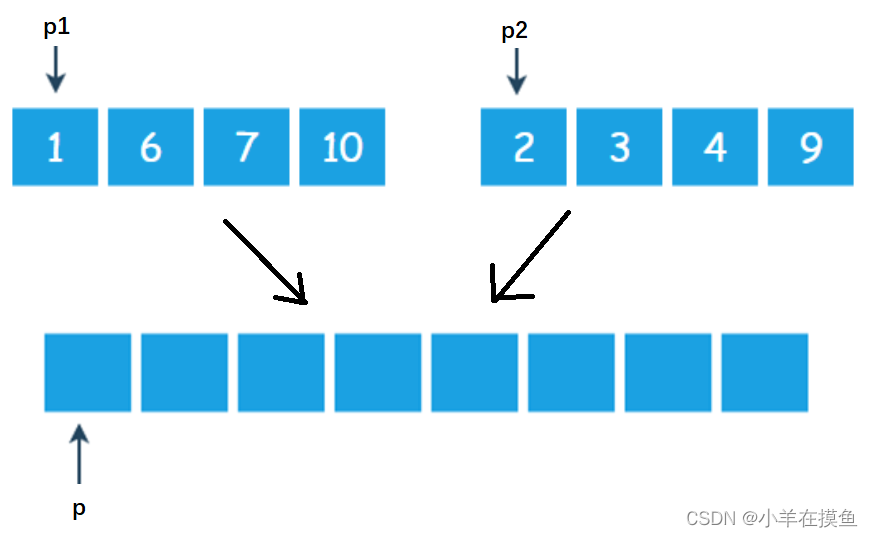
用上述长度为4的集合举例:
第一步:比较p1和p2位置元素的大小,谁的小,将谁的值放到p位置,并将指向小的元素的那个指针++,并且将p++
1比2小,放1到p位置,p1++,p++
......
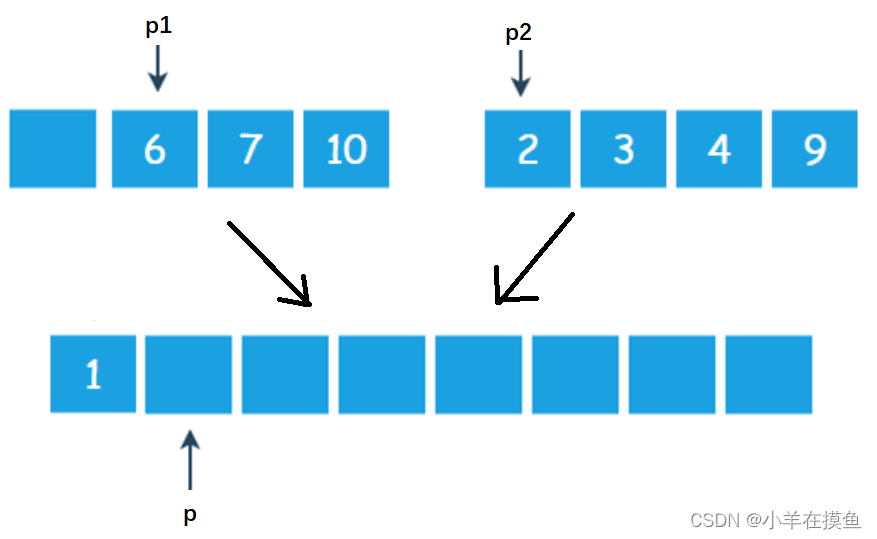
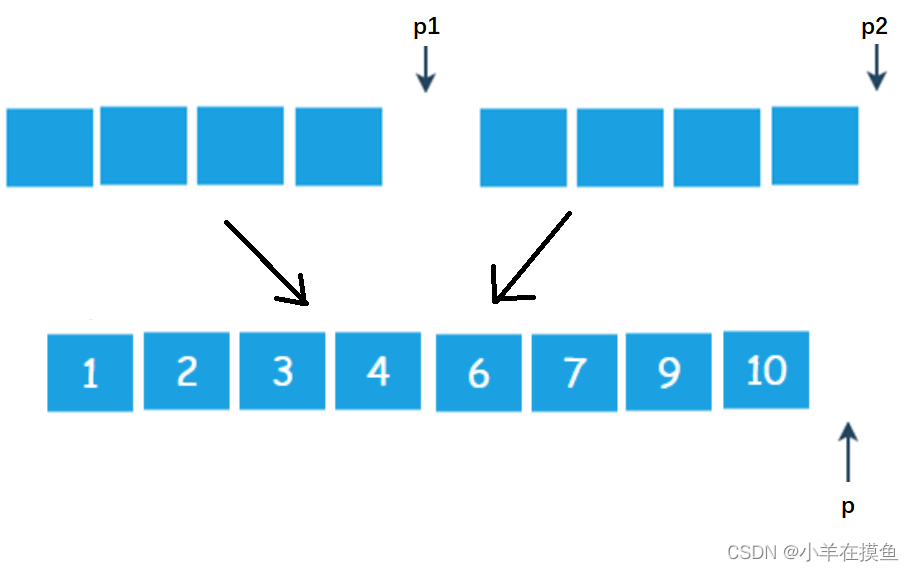
第二步:按第一步的步骤,逐一比较,直到有一个指针走到了集合之外如下:
此时p2已经走到了集合外,就可以退出循环了
第三步:放一个循环,将没走完的那个集合的剩余元素按顺序放到大集合种即可
当p走到大集合外面时结束循环
3.代码实现(递归方式):
//归并排序(递归实现)
//归并子函数
//(在遇到需要malloc扩容的函数时,将malloc代码放入主函数,另写一个子函数用来完成递归)
void _MergeSort(int* a, int begin ,int end, int* temp)
{
//最后只剩下一个数的时候就说明begin=end,返回
if (begin >= end)
{
return;
}
int mid = (begin + end) / 2;
//[begin, mid] [mid+1, end] 递归让子区间都有序
_MergeSort(a, begin, mid, temp); //递归左半区
_MergeSort(a, mid+1, end, temp); //递归右半区
//归并
int begin1 = begin, end1 = mid; //左区间[begin1, end1]
int begin2 = mid + 1, end2 = end; //右区间[begin2, end2]
int i = begin;
//如果左右两个区间都没有结束就继续,只要有一个区间结束就终止
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
{
temp[i++] = a[begin1++];
}
else
{
temp[i++] = a[begin2++];
}
}
//将没走到头的区间按顺序放到后面
while (begin1 <= end1)
{
temp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
temp[i++] = a[begin2++];
}
//将临时区间的数据拷贝回原数组
memcpy(a + begin, temp + begin, sizeof(int) * (end - begin + 1));
}
//归并主函数
void MergeSort(int* a, int n)
{
int* temp = (int*)malloc(sizeof(int) * n);
if (temp == NULL)
{
perror("malloc fail");
exit(-1);
}
_MergeSort(a, 0, n-1, temp);
free(temp);
temp = NULL;
}归并排序的非递归方式
原理:
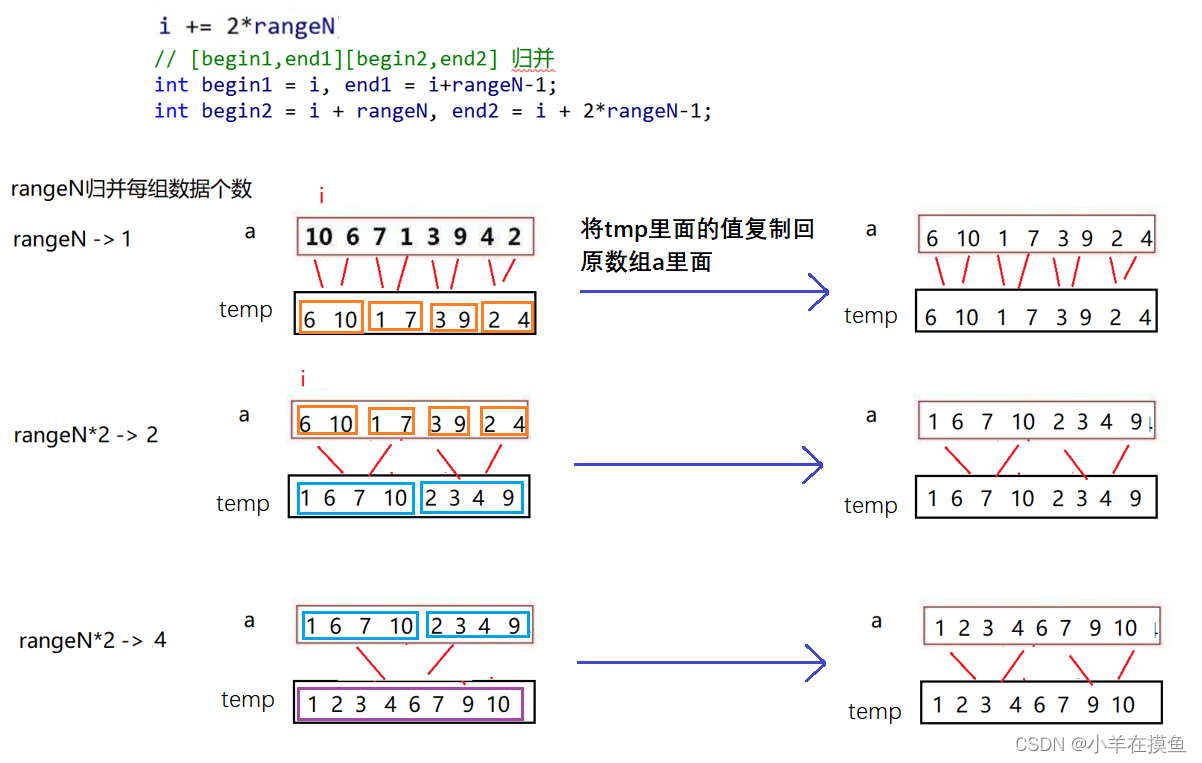
控制每次参与归并的元素即可,可以先定义一个变量rangeN,让其来划分区域
开始时rangeN=1,区域为1则是有序,
i = i + 2*rangeN 定义 i 来区分每块区域
左区域:[begin1,end1] 右区域:[begin2,end2]
上图情况是一个特殊情况,如果遇到不能被完全划分左右区域对称的情况分为以下三种:
情况1:
当最后一个区域进行归并时,最后一组的左区间越界,所以需要对左区间的end1进行控制
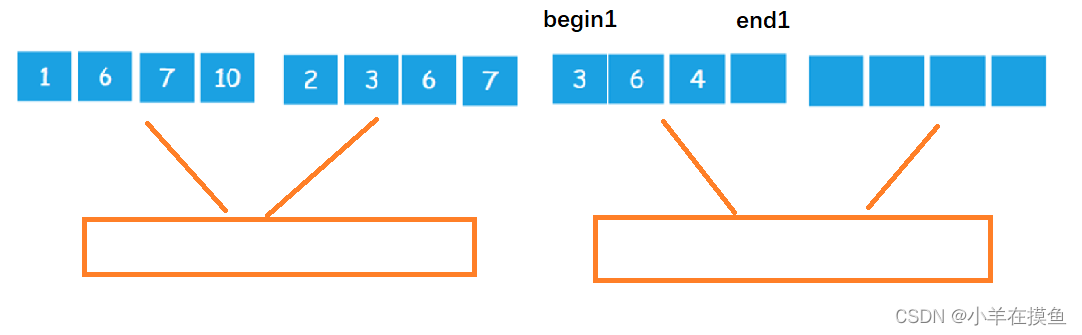
情况2:
当最后一个区域进行归并时,最后一组的右区间全部越界,所以需要对右区间的begin2进行控制
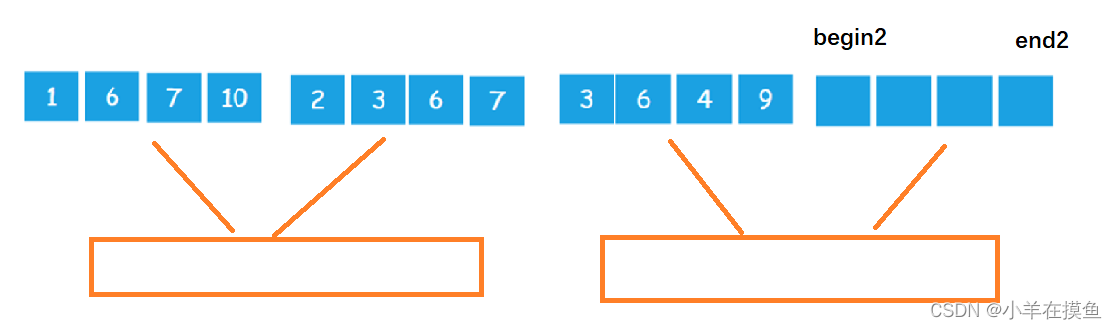
情况3:
当最后一个小组进行归并时,由于右区间越界,所以我们需要对右区间end2进行控制
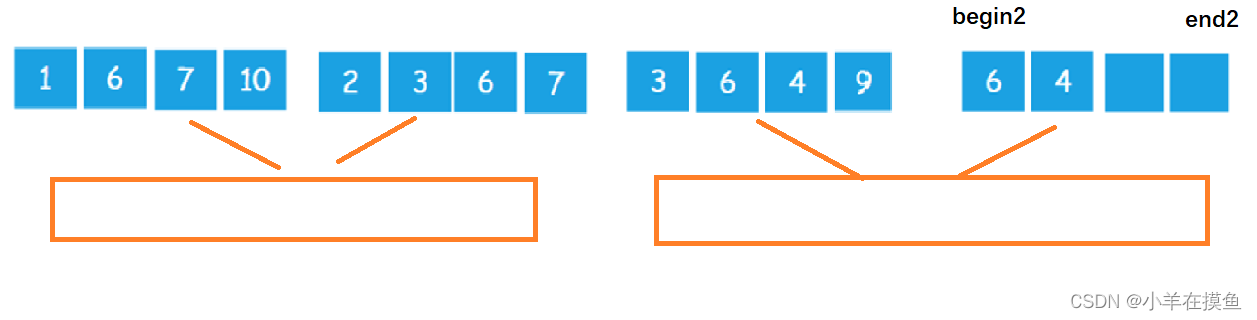
非递归代码实现
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int)*n);
if (tmp == NULL)
{
perror("malloc fail");
exit(-1);
}
// 归并每组数据个数,从1开始,因为1个认为是有序的,可以直接归并
int rangeN = 1;
while (rangeN < n)
{
for (int i = 0; i < n; i += 2 * rangeN)
{
// [begin1,end1][begin2,end2] 归并
int begin1 = i, end1 = i + rangeN - 1;
int begin2 = i + rangeN, end2 = i + 2 * rangeN - 1;
int j = i;
// end1 begin2 end2 越界的三种情况
//一定需要按顺序进行判断,不然会出错
//end1越界,情况1,
//解决:直接退出本次循环,可以不让后面的进行归并,再下一次循环时再排序
if (end1 >= n)
{
break;
}
//begin2出界,情况2,
//解决:直接退出本次循环,可以不让后面的进行归并,再下一次循环时再排序
else if (begin2 >= n)
{
break;
}
//end2越界,情况3
//解决:让end2等于数组最后的下标
else if (end2 >= n)
{
end2 = n - 1;
}
//开始按顺序归并
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
// 归并一部分,拷贝一部分
memcpy(a + i, tmp + i, sizeof(int)*(end2 - i + 1));
}
rangeN *= 2;
}
free(tmp);
tmp = NULL;
}归并排序的特性总结:
- 归并的缺点在于需要O(N)的空间复杂度,
归并排序的思考更多的是解决在磁盘中的外排序问题。- 时间复杂度:O(N*logN)
- 空间复杂度:O(N)
- 稳定性:稳定
排序算法复杂度及稳定性分析
什么时稳定性?
稳定性的价值:
比如再考试排名的时候,第三名种有三个人的成绩相同,那么如果先交卷的人是第三名的话,就要去再成绩排序的时候保证其稳定性
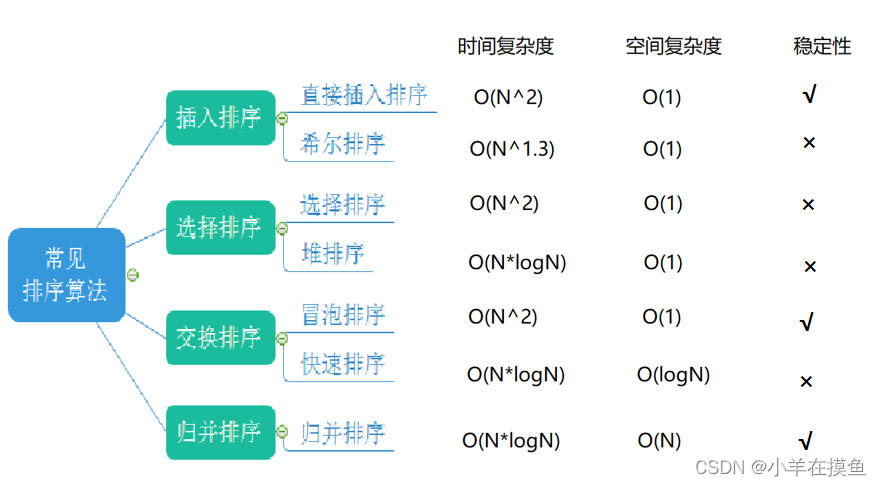
各种常见排序算法的总结







![149.网络安全渗透测试—[Cobalt Strike系列]—[HTTP Beacon重定器/代理服务器/流量走向分析]](https://img-blog.csdnimg.cn/d4ee09eb4dee4952b7bb36dc60bbac1b.gif)