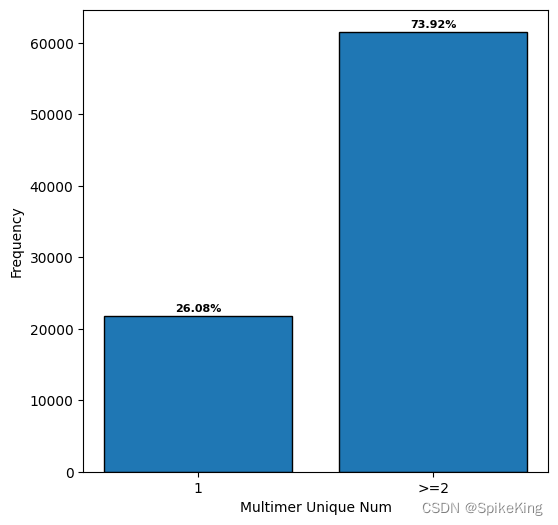
堆栈模型
JS 代码执行时,值类型变量存储在栈,引用类型变量存储在堆。
// 变量 a 存储在栈里
let num1 = 1
let num2 = num1
num2 = 2
// 这时打印 num1 是 1,num2 是 2。
// { a: 1 } 存在堆里,obj1 只是一个指针引用
let obj1 = { a: 1 }
// 这时一个叫 obj2 的指针也指向了这个堆
let obj2 = obj1
// 修改数据是修改的堆的数据,所以 obj1 和 obj2 的结果都会变
obj2.a = 2
// 这时打印 obj1 是 { a: 2 },num2 是 { a: 2 }。
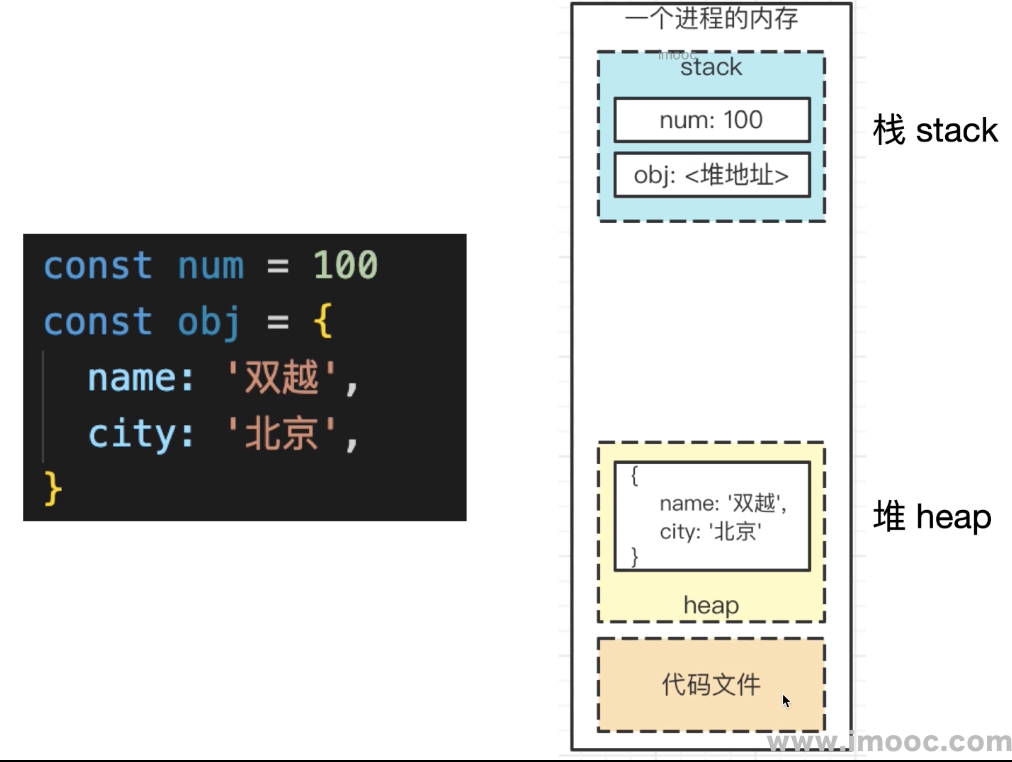
堆和二叉树
堆是一个完全二叉树
最大堆:父节点 >= 子节点
最小堆:父节点 <= 子节点
比如:父节点 10 小于所有的子节点,父节点 14、25 也小于所有的子节点
完全二叉树
若设二叉树的高度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第h层有叶子结点,并且叶子结点都是从左到右依次排布。
所以一个满二叉树一定是完全二叉树。
那么为什么要设计最大堆最小堆呢?
答:堆的逻辑结构是二叉树,物理结构是数组
数组:适合连续存储、节省空间
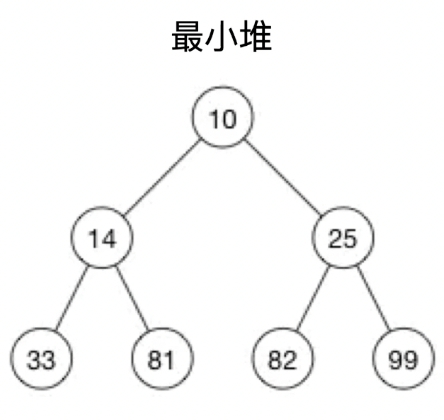
比如上图就是一个最小堆,我们用数组表示
// 忽略 0 节点 -1
const arr = [-1, 10, 14, 25, 33, 81, 82, 99]
那么我们如果要找某一项的关系节点怎么找呢,由于这是一个最小堆,这是有规律的
// 节点关系
const parentIndex = Math.floor(i / 2)
const leftIndex = 2 * i
const rightIndex = 2 * i + 1
知道了这个关系,找到对应的值会很快,就行数组找 index 的值一样,复杂度 O(1)
堆的特点
- 查询比 BST(平衡搜索树) 慢。因为规则简单,不像 BST 左边一定比右边小。但是堆的使用场景就是堆栈模型,而堆栈模型是直接通过指针引用(这个指针已经知道了是哪个index了),不用遍历查找。所以还是很快。
- 删除比 BST 快,维持平衡更快,原因同上规则简单。