一、树状数组

树状数组给人的感觉就像，一直在维护前缀和一样，只是加快了前缀和的速度，再用前缀和结合题目得出一些性质，从而去解题。（一些不成熟的看法）

基础知识（一般树状数组用来处理单点修改，区间查询）单个操作时间复杂度是O(logn)

对于（区间修改，单点查询）（区间修改，区间查询）后续更新。

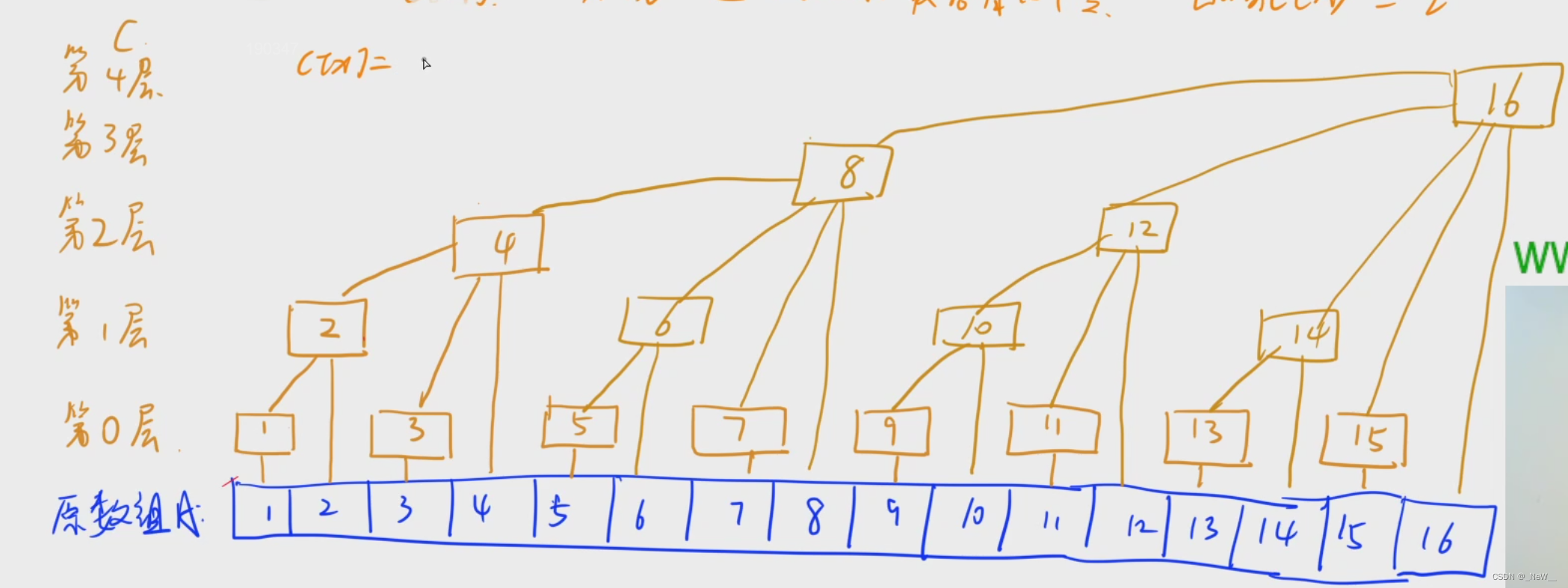
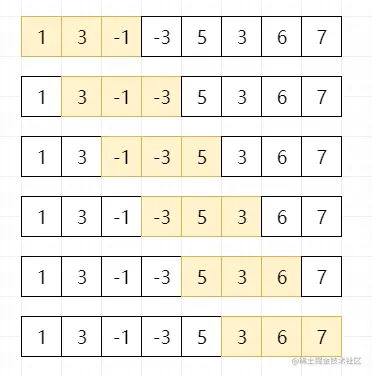
 这张图是树状数组的核心

图上有的点表示只有这个点的值，比如奇数都只表示自己的点，因为奇数的二进制最后一位都是1，偶数表示若干个点的和，比如8表示5~8的和

树状数组的好处就是，想要知道某个数的前缀和，不需要把所有点都加上，比如想要知道前8个数的和，只需要加上c[8],c[4],c[2]就行。

树状数组还有一个最重要的知识点是lowbit()函数

 1、动态求连续区间和

这道题就是标准的单点修改，区间查询 

代码：

#include<iostream>
#include<cstdio>

using namespace std;
const int N = 1e5 + 10;

int a[N],c[N];
int n,m;
int lowbit(int x)
{
    return x&(-x);
}

int add(int x,int v)
{
    for(int i=x;i<=n;i += lowbit(i)) c[i]+=v;
}

int query(int x)
{
    int res=0;
    for(int i=x;i>0;i -= lowbit(i)) res+=c[i];
    
    return res;
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) 
    {
        scanf("%d",&a[i]);
        add(i,a[i]);
    }
    while(m--)
    {
        int k,a,b;
        scanf("%d%d%d",&k,&a,&b);
        
        if(k==1) add(a,b);
        else printf("%d\n",query(b)-query(a-1));
        
    }
    
    return 0;
}

函数解释：

add(a,b) ： 表示从a开始到n所有和a有关的点都加上b

example： a=9，那么10，12 ，16 都要加上b

query(x) : 表示前x个数的和 

2、数星星

 分析：根据输入方式，可以把二维变为一维，可以把样例模拟一下，（把4，5纵向压倒第一层，也就是最下边这一层）每次输入星星时，根据x数组，把该星星之前的星星都加上就行，这样就可以把问题转化为求前缀和，又因为该题需要一边输入星星，一边求·该星星的值，所以不能用朴素的求前缀和问题，朴素前缀和问题时间复杂度时O(n)的，所以需要树状数组来求。

#include<iostream>
#include<cstdio>

using namespace std;

const int N = 32010;
int n,m;
int tr[N];
int level[N];

int lowbit(int x)
{
    return  x& (-x);
}

void add(int x)
{
    for(int i=x;i<N;i+=lowbit(i)) tr[i]++;
}

int sum(int x)
{
    int res=0;
    for(int i=x;i>0;i-=lowbit(i)) res+=tr[i];
    return res;
}

int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        
        x++;
        level[sum(x)]++;
        add(x);
    }
    for(int i=0;i<n;i++) printf("%d\n",level[i]);
    return 0;
}

 楼兰图腾

 正常思路会想到这道题，可以求每一个中间点的左右满足条件的点，然后相乘，但是左右两边的点怎么预处理出来呢？

此时可以想到树状数组（没学树状数组之前，根本想不到怎么预处理）

 可以用树状数组求每个yi在1~n出现的次数

先从左往右预处理出来，每一个比yi大或者小的数出现的次数，

清空一下树状数组再，从右往左预处理每一个比yi大或者小的数，然后左右相乘

代码

#include<iostream>
#include<cstring>

using namespace std;
typedef long long LL;

const int N = 2e5 + 10;

int gre[N],lower[N];
int tr[N];
int n;
int s[N];

int lowbit(int x)
{
    return x&(-x);
}

void add(int x,int c)
{
    for(int i=x;i<=n;i+=lowbit(i)) tr[i]+=c; 
}

int sum(int x)
{
    int res=0;
    for(int i = x;i>0;i-=lowbit(i)) res+=tr[i];
    
    return res;
}
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++) scanf("%d",&s[i]);
    
    for(int i=1;i<=n;i++)
    {
        int y=s[i];
        gre[i]=sum(n)-sum(y);//求y+1~n的数的个数
        lower[i]=sum(y-1);求1~y-1的数的个数
        add(y,1);//当前y的个数加1
    }
    
    memset(tr,0,sizeof tr);
    LL res1=0,res2=0;
    for(int i=n;i>0;i--)
    {
        int y=s[i];
        res1+=gre[i]*(LL)(sum(n)-sum(y));
        res2+=lower[i]*(LL)(sum(y-1));
        add(y,1);//当前y的个数加1
    }
    
    cout<<res1<<" "<<res2<<endl;
    return 0;
}

 一个简单的整数问题（区间修改，单点查询）把原数组处理为差分数组

 这道题是区间修改，单点查询

运用了差分的思想，差分的概念:

b1=a1-a0
b2=a2-a1
b3=a3-a2
...
bn=an-a(n-1)

 运用差分就可以把区间修改从O(n)的时间复杂度转换为O(logn)

这道题把树状数组预处理为差分数组，那么知道一个点的数值，就可以前缀和求出该点的数值，又因为用的是树状数组，那么在O(logn)的时间下就可以处理出来。

#include<iostream>
#include<cstring>

using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
int a[N];
LL b[N];
int n,m;
int lowbit(int x)
{
    return x&(-x);
}

void add(int x,int c)
{
    for(int i=x;i<=n;i+=lowbit(i)) b[i]+=c;
}

LL sum(int x)
{
    LL res=0;
    for(int i=x;i>0;i-=lowbit(i)) res+=b[i];
    return res;
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) scanf("%d",&a[i]),add(i,a[i]-a[i-1]);//预处理差分数组
    
    char op[2];
    while(m--)
    {
        int l,r,d;
        scanf("%s%d",op,&l);
        if(*op=='Q') printf("%lld\n",sum(l));//求前缀和
        else 
        {
            scanf("%d%d",&r,&d);
            add(l,d);//差分思想
            add(r+1,-d);
        }
    }
    return 0;
}

  一个简单的整数问题2（区间修改，区间查询）把原数组处理为差分数组

 

 

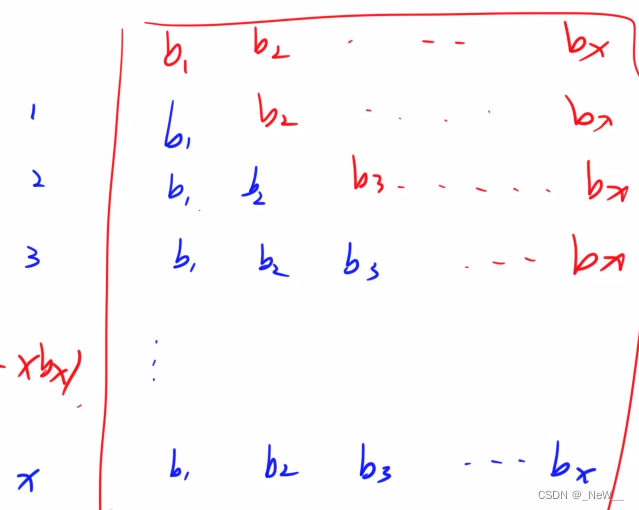
 本题较上一题加了一项是区间查询，暴力查询绝对会超时，所以要推结论

上图就是腿的结论，蓝色的代表所求的，红色代表多余的。

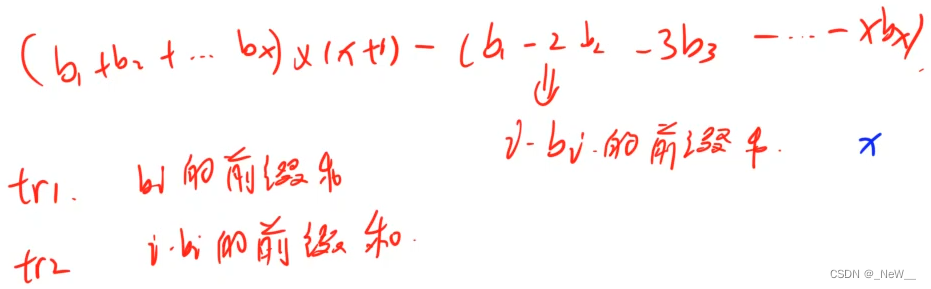
最终可以得出上边这个结论：每一行蓝色的bi，加起来就是ai，所以所有行的蓝色bi加起来就是a的前缀和，为了方便计算可以加上另一部分，最后再减去，红色部分，显而易见，是1*b1+2*b2+3*b3+.......+x*bx ，此时我们可以在维护一个数组st2，用来预处理i*bi

代码

#include<bits/stdc++.h>

using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
LL tr1[N],tr2[N];
int a[N];
int n,m;

int lowbit(int x)
{
    return x&(-x);
}
void add(LL tr[],int x,LL c)
{
    for(int i=x;i<=n;i+=lowbit(i)) tr[i]+=c;
}
LL sum(LL tr[],int x)
{
    LL res=0;
    for(int i=x;i>0;i-=lowbit(i)) res+=tr[i];
    return res;
}
LL pre_sum(int x)
{
    return sum(tr1,x)*(x+1)-sum(tr2,x);
}
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++) scanf("%d",&a[i]);
    for(int i=1;i<=n;i++)
    {
        int b=a[i]-a[i-1];
        add(tr1,i,b);
        add(tr2,i,(LL)b*i);
    }
    while(m--)
    {
        char op[2];
        int l,r,d;
        scanf("%s%d",op,&l);
        if(*op=='Q')
        {
            scanf("%d",&r);
            printf("%lld\n",pre_sum(r)-pre_sum(l-1));
        }
        else
        {
            scanf("%d%d",&r,&d);
            add(tr1,l,d),add(tr1,r+1,-d);
            
            add(tr2, l, (LL)l*d),add(tr2, r+1, (r+1)*(-d));
        }
    }
    
    return 0;
}

 树状数组的应用

 本题是利用树状数组来维护前缀和

从后往前遍历，那么假如第i头牛，前面比他高的数量是k，那么这头牛就是，第k+1小（在1~n中还没用过的数）的牛

初始时1~n每个数是1，没用去一个数，则把这个数删去，

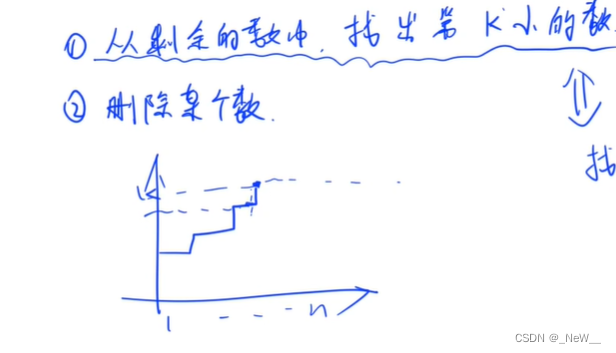
 根据上图我们发现可以，用二分来查找第k+1小的数。

#include<bits/stdc++.h>

using namespace std;

const int N = 1e5 + 10;

int h[N];
int tr[N];
int ans[N];
int n;
int lowbit(int x)
{
    return x&(-x);
}

void add(int x,int c)
{
    for(int i=x;i<=n;i+=lowbit(i)) tr[i]+=c;
}
int sum(int x)
{
    int res=0;
    for(int i=x;i;i-=lowbit(i)) res+=tr[i];
    return res;
}
int main()
{
    cin>>n;
    for(int i=2;i<=n;i++) scanf("%d",&h[i]);
    
    for(int i=1;i<=n;i++) add(i,1);
    for(int i=n;i;i--)
    {
        int k=h[i]+1;
        int l=1,r=n;
        while(l<r)
        {
            int mid=l+r>>1;
            if(sum(mid)>=k) r=mid;
            else l=mid+1;
        }
        ans[i]=l;
        add(l,-1);//将当前这个点删去
        
    }
    for(int i=1;i<=n;i++) cout<<ans[i]<<endl;
    return 0;
}

二、线段树

树状数组能写的题线段树都能写，但线段树代码比较麻烦。

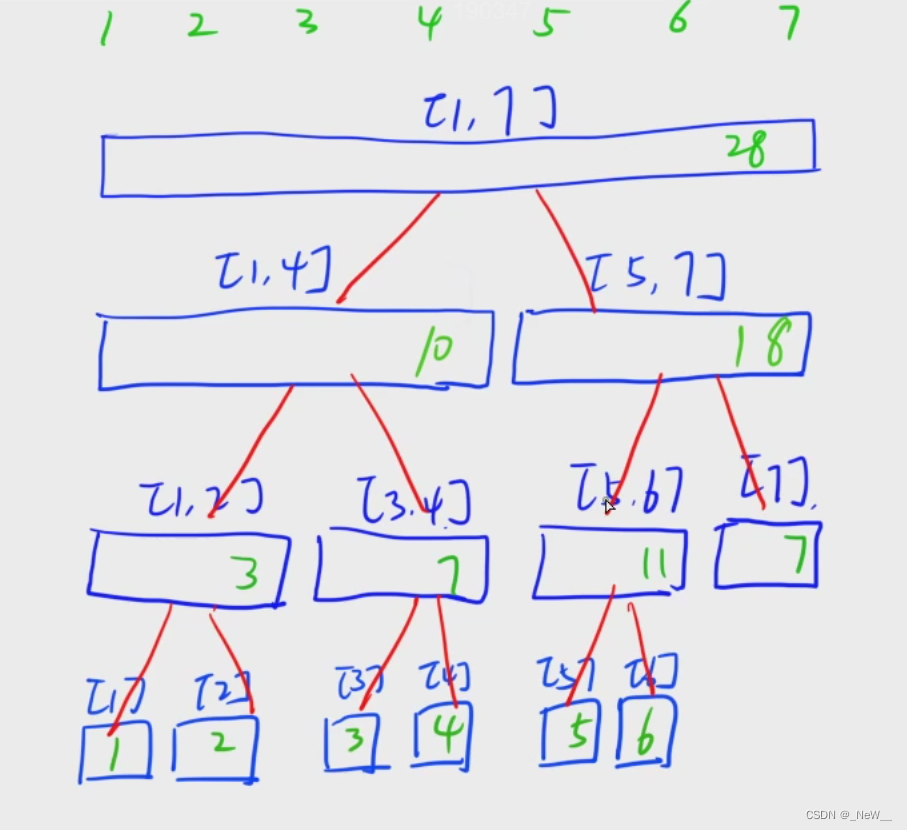
 上图以区间和来举例：

线段树的主要思想是：把一个数组分位若干个小区间（并且每个小区间都有编号，根据经验标号一般不会超过4*n)，再根据题目要求维护区间的特性。

1、上面的  动态求连续区间和

#include<iostream>
#include<cstdio>

using namespace std;

const int N = 1e5 + 10;

int w[N];

struct Node{
    int l,r;
    int sum;
}tr[N*4];

int n,m;
void pushup(int u)
{
    tr[u].sum=tr[u<<1].sum+tr[u<<1|1].sum;
}

void built(int u,int l,int r)
{
    if(l==r) tr[u]={l,r,w[l]};
    else
    {
        tr[u]={l,r};
        int mid=l+r >>1;
        built(u<<1,l,mid),built(u<<1|1,mid+1,r);
        pushup(u);
    }
}

void modify(int u,int x,int v)
{
    if(tr[u].l==tr[u].r) tr[u].sum+=v;
    else
    {
        int mid=tr[u].l+tr[u].r>>1;
        if(x<=mid) modify(u<<1,x,v);
        else modify(u<<1|1,x,v);
        pushup(u);
    }
}
int query(int u,int l,int r)
{
    if(tr[u].l>=l && tr[u].r<=r) return tr[u].sum;
    
     int mid=tr[u].l+tr[u].r>>1;//写这道题时，在想为什么要用mid来确定范围，而不是直接用 
                               //tr[u].l和tr[u].r确定，因为mid可以直接判断下边两个儿子是否会 
                               //被用到
    int sum=0;
    if(l<=mid) sum+=query(u<<1,l,r);
    if(r>mid) sum+=query(u<<1|1,l,r);

    return sum;
}
int main()
{
    scanf("%d%d",&n,&m);
    
    for(int i=1;i<=n;i++) scanf("%d",&w[i]);
    built(1,1,n);
    
    while(m--)
    {
        int k,a,b;
        scanf("%d%d%d",&k,&a,&b);
        if(k==1) modify(1,a,b);
        else printf("%d\n",query(1,a,b));
    }
    
    return 0;
}