目录

1.相关概念

2.马尔可夫链的状态概率分布推演及稳态分布

3.马尔可夫链的应用

4.稳态分布性质

---

1.相关概念

小明同学每日选择早餐的概率转化如下图所示： 

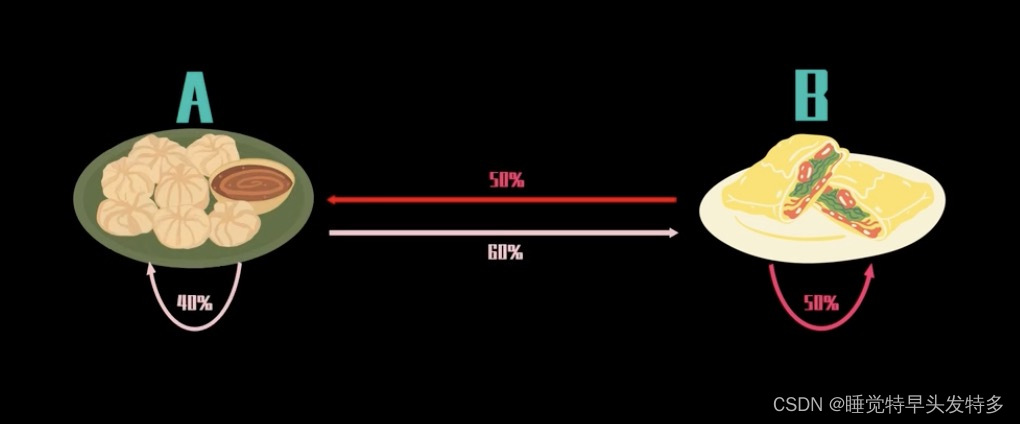
 并且当日的选择只受前一日的结果以及对应的转移概率影响，与之前的选择无关。———>             马尔可夫链的核心三要素：(1)状态空间 State Space，即早餐空间只能来自A、B两空间其一。(2)无记忆性 Memorylessness，即当期选择的概率只受上期状态影响。用公式表达：(3)转移矩阵Transition Matrix。

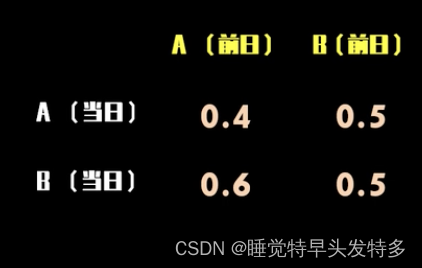
2.马尔可夫链的状态概率分布推演及稳态分布

假如小明同学第一天选择早餐A，那么当天的状态概率分布为[1,0]；

将其与转移矩阵相乘可以得到第二天的状态概率分布为[0.4,0.6]；

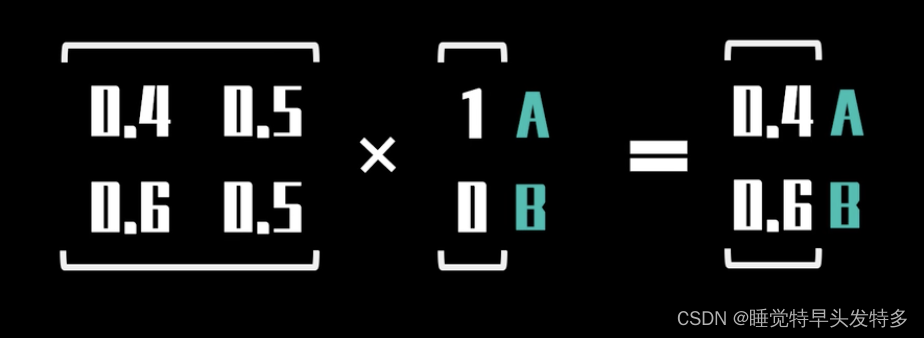
重复同样的操作，可以得到第三天的状态概率分布为[0.46,0.54] ；

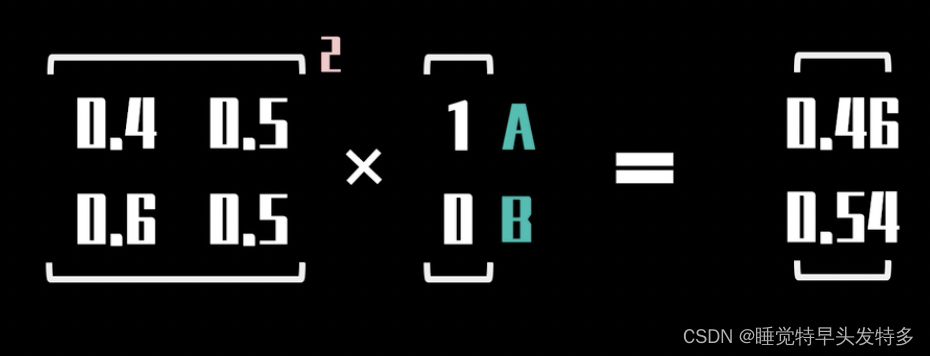
继续推演下去，我们可以得到稳态分布steady state distribution： [0.454545,0,545454]

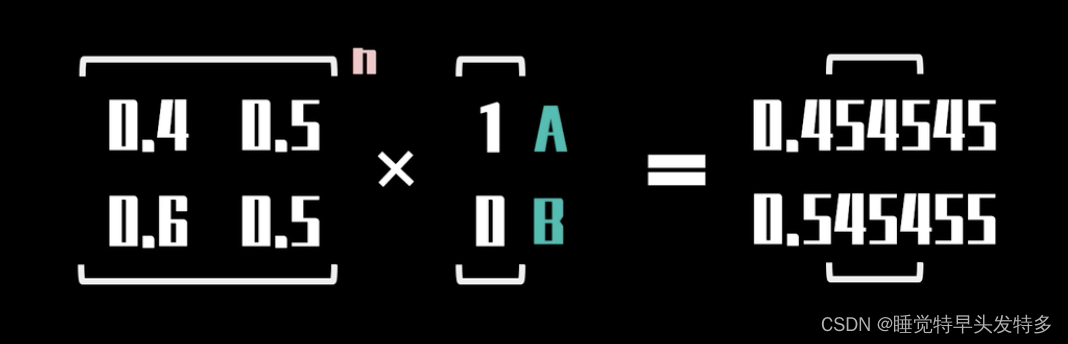
 假如小明第一天选择早餐B，稳态分布不变， 将state A和stateB设置为非负且相加和为一的任意值，稳态分布唯一，说明在该马尔可夫链下，最终的稳态是不受初始状态影响的。

但是，需要注意的是，并不是所有的马尔可夫链都具有唯一的稳态分布。

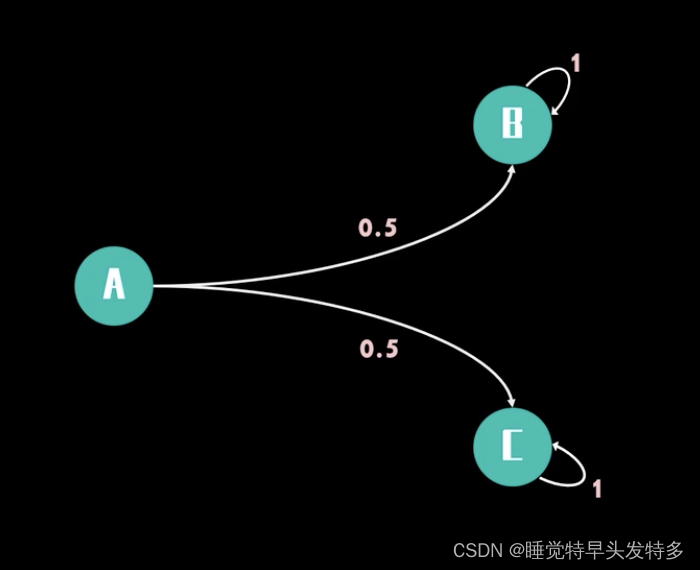
如上图中的马尔可夫链，A状态进入B或C状态之后，均在对应状态下自循环，无法达到其他状态。 

3.马尔可夫链的应用

(1)在自然语义处理方面，我们可以利用字符、词语之间的转移矩阵，去联想用户接下来想说什么、想搜索什么。

(2)可以利用马尔可夫链，随机生成诗词、文章等。

(3)在金融行业，马尔可夫链可以用于分析牛市、熊市状态转换，股票价格预测，信用评级等等。

4.稳态分布性质

大数定理 Law of Large Numbers ～ 稳态分布

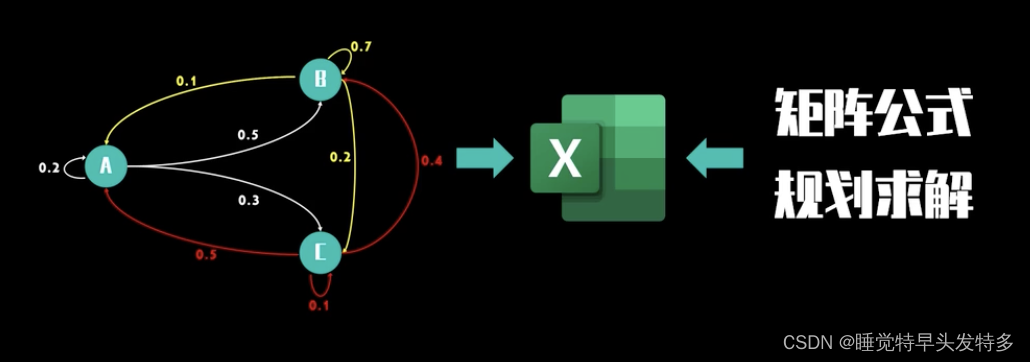
EXCEL中的数组函数可以解决马尔可夫链相关问题；

符合唯一稳态分布的马尔可夫链：

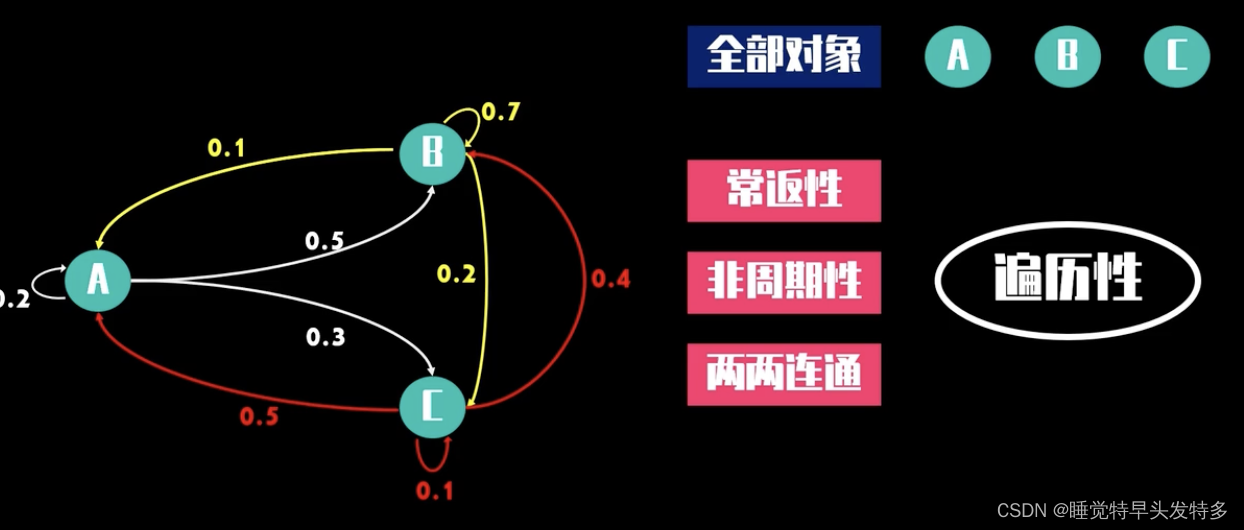
常返性recurrent和它的对立面暂时性transient放在一起理解， 常返性：可以进入新状态也可以按路径返回；

具有常返性、非周期性、两两联通三个特点的马尔可夫链具有遍历性，即具有唯一的稳态分布。

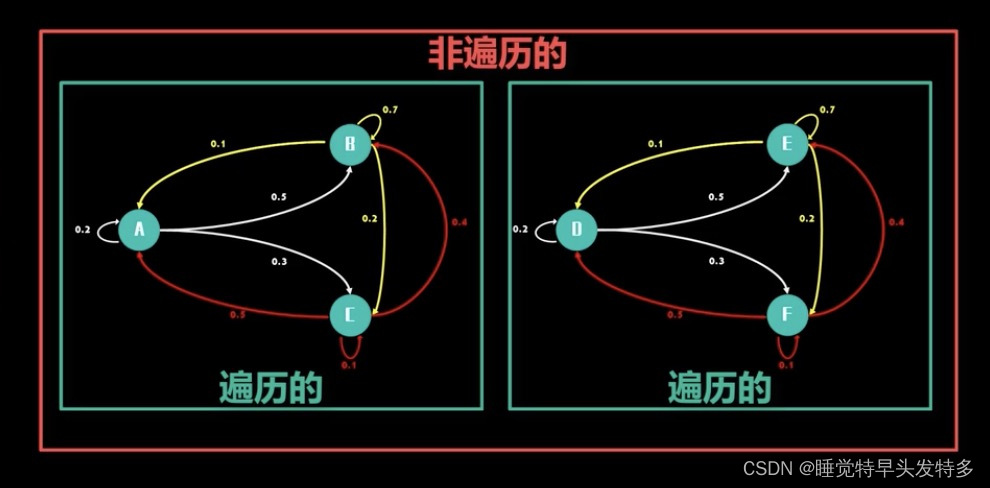
上图两个独立的马尔可夫链都是遍历的，但是作为一个整体便不再遍历，因为ABC节点与DEF节点非两两连通。 

学习参考：【数之道 18】"马尔可夫链"是什么？了解它只需5分钟！_哔哩哔哩_bilibili