基于粒子群算法的线性规划问题求解matlab程序
1 基本粒子群算法流程
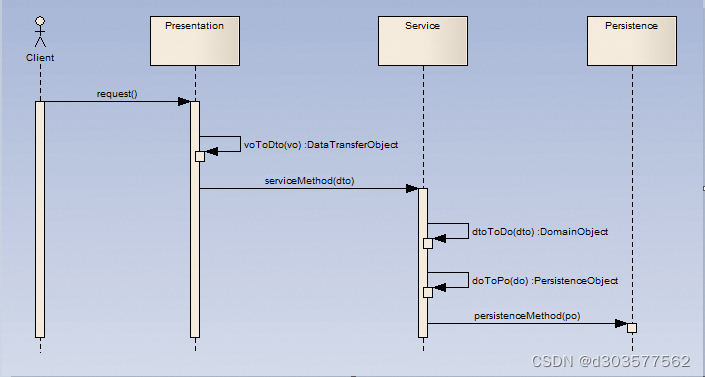
粒子群算法基于“种群”和“进化”的概念,通过个体间的协作与竞争,实现复杂空间最优解的搜索,其流程如下:
(1)初始化粒子群,包括群体规模 NN,每个粒子的位置 xixi 和速度 vivi。
(2)计算每个粒子的适应度值 fit[i]fit[i]。
(3)对每个粒子,用它的适应度值 fit[i]fit[i] 和个体极值 pbest(i)pbest(i) 比较。如果 fit[i]>pbest(i)fit[i]>pbest(i),则用 fit[i]fit[i]替换掉 pbest(i)pbest(i)。
(4)对每个粒子,用它的适应度值 fit[i]fit[i] 和全局极值 gbestgbest 比较。如果 fit[i]>gbestfit[i]>gbest 则用 fit[i]fit[i]替换掉 gbestgbest。
(5)迭代更新粒子的速度 vivi 和位置 xixi。
(6)进行边界条件处理。
(7)判断算法终止条件是否满足:若是,则结束算法并输出优化结果;否则返回步骤(2)。
基本粒子群算法的算法流程图如下图所示:

2 线性规划算例

3 粒子群算法求解结果
1)迭代曲线

2)求解

4 matlab程序
1)主函数
% 粒子群算法版
clc;
clear;
close all;
%% 算法参数
nVar=3; %变量个数
VarMin=ones(1,3)*0; % 变量下限
VarMax=ones(1,3)*15; % 变量上限
MaxIt=60; % 最大迭代次数
nPop=100; % 种群规模
%% 计算
[ bestPosition, fitValue ] = PSOFUN( @fun_objective,nVar,VarMin,VarMax,MaxIt,nPop );
%% 输出
display(['粒子群算法获得的最优变量为 : ', num2str(bestPosition)]);
display([' 获得的最优目标函数: ', num2str(fitValue)]);
。。。。。。。略