目录

二叉搜索树

二叉搜索树的一些操作函数 

二叉搜索树的查找操作Find

递归实现

迭代实现 

查找最大和最小元素

查找最小元素的递归函数

查找最大元素的迭代函数 

---

二叉搜索树

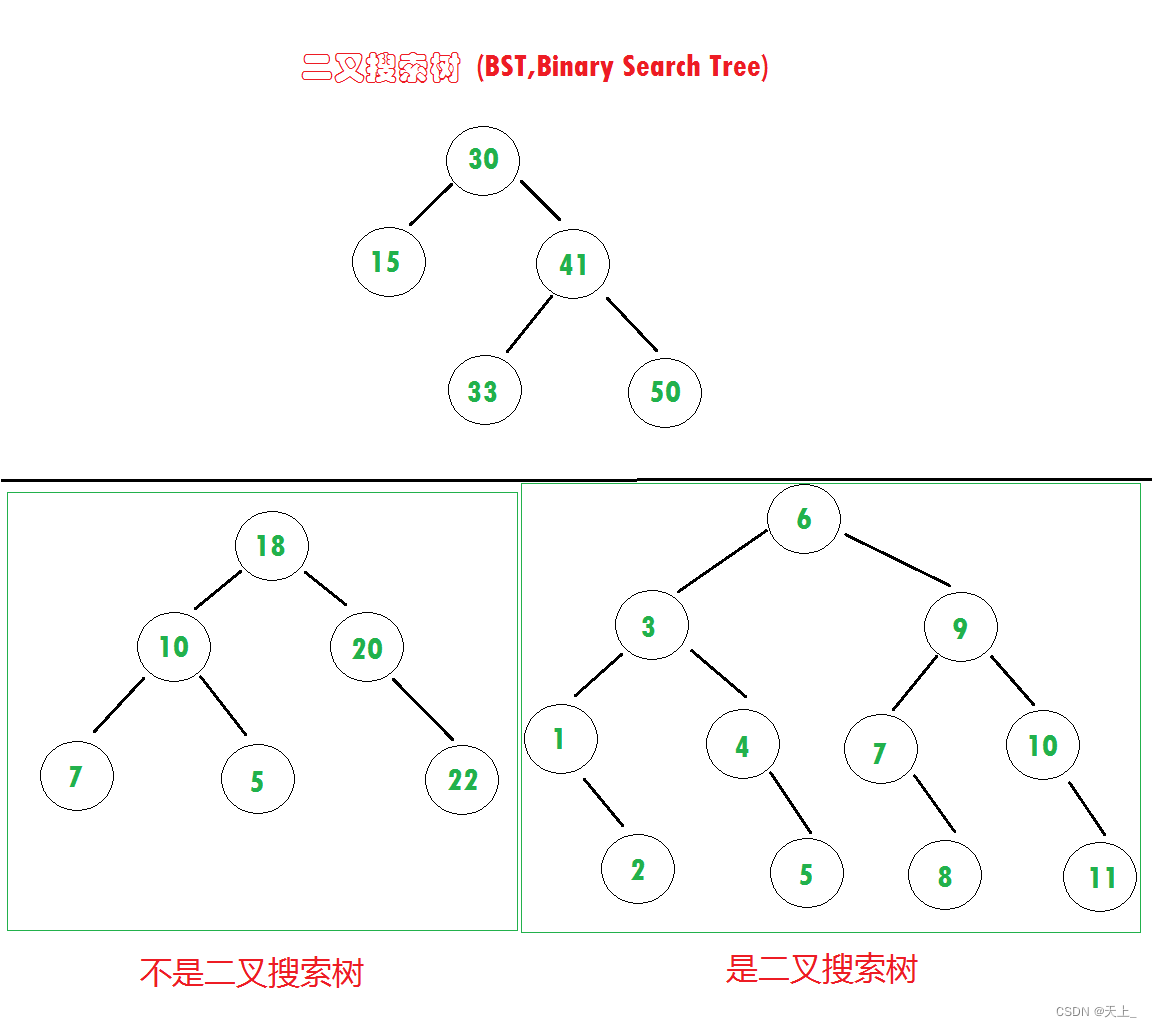
二叉搜索树（BST，Binary Search Tree），也称二叉排序树或二叉查找树。

一颗二叉树，可以为空；如果不为空，满足一下性质：

1.非空左子树的所有键值小于其根节点的键值。

2.非空右子树的所有键值大于其根节点的键值。

3.左、右子树都是二叉搜索树。

 

二叉搜索树的一些操作函数 

• Position Find （ElementType x，BinTree BST）；

从二叉搜索树BST中查找元素x，返回其所在节点的地址。

• Position FindMin（BinTree BST）；

从二叉搜索树BST中查找并返回最小元素所在节点的地址。

• Position FindMax（BinTree BST）；

从二叉搜索树BST中查找并返回最大元素所在节点的地址。

• BinTree Insert（ElementType x，BinTree BST）；

在二叉搜索树BST中插入一个值为x的节点。

• BinTree Delete（ElementType x，BinTree BST）；

在二叉搜索树BST中删除值为x的节点。

二叉搜索树的查找操作Find

二叉搜索树的查找思路很简单：

查找从根节点开始，如果树为空，返回NULL；

若搜索树非空，则根节点关键字和x进行比较，并进行不同处理：

1. 若x小于根节点键值，只需在左子树中继续搜索；
2. 若x大于根节点键值，则在右子树中进行继续搜索；
3. 如果两者比较的结果是相等，搜索完成，返回指向此节点的指针。

递归实现

使用递归的方法实现的话，代码很简单，直接判断键值大小，进行尾递归。（即在程序要返回值时进行递归）

Position Find(ElementType x,BinTree BST)
{
	if (!BST)
	{
		return NULL;  //为空则查找失败
	}
	if (x > BST->data)
	{
		return Find(x, BST->Right);  //在右子树中继续查找
	}
	else if (x < BST->data)
	{
		return Find(x, BST->Left);   //在左子树中继续查找
	}
	else   //x == BST->data
	{
		return BST;                  //查找成功，返回结点地址
	}
}

但递归实现的方法效率不是很高，从编译的角度来看，尾递归可以用循环的方式来实现了。

所以我们将递归函数改为迭代函数

迭代实现 

 与递归函数同样的一步是，先判断节点是否为空，为空表示查找失败，非空则开始查找；

如果x的值大于根节点，就将节点的指针指向右子树继续循环查找；

如果x的值小于根节点，则将节点的指针指向左子树继续循环查找；

如果相等，则说明查找成功了。

Position IterFind(ElementType x, BinTree BST)
{
	while (BST)
	{
		if (x > BST->data)
		{
			BST = BST->Right;    //向右子树中移动，继续查找
		}
		else if (x < BST->data)
		{
			BST = BST->Left;     //向左子树中移动，继续查找
		}
		else
		{
			return BST;          //查找成功，返回结点地址
		}
	}
	return NULL;                 //查找失败
}

但是这个查找的效率决定于树的高度。

如果二叉搜索树排成了一条链，即斜二叉树，他的这颗树的高度就为n-1，这样最坏的情况下要找到一个节点就需要n-1次了。算法的时间效率就只有O（N）了，而达不到我们想要的log2n，要解决这个问题就要涉及到以后要讲的平衡二叉树了。

查找最大和最小元素

因为二叉搜索树的特殊性，比根节点小的在左子树，比根节点大的在右子树。

所以，

最大元素一定是在树的最右分枝的端节点上； 最小元素一定是在树的最左分枝的端节点上。

 

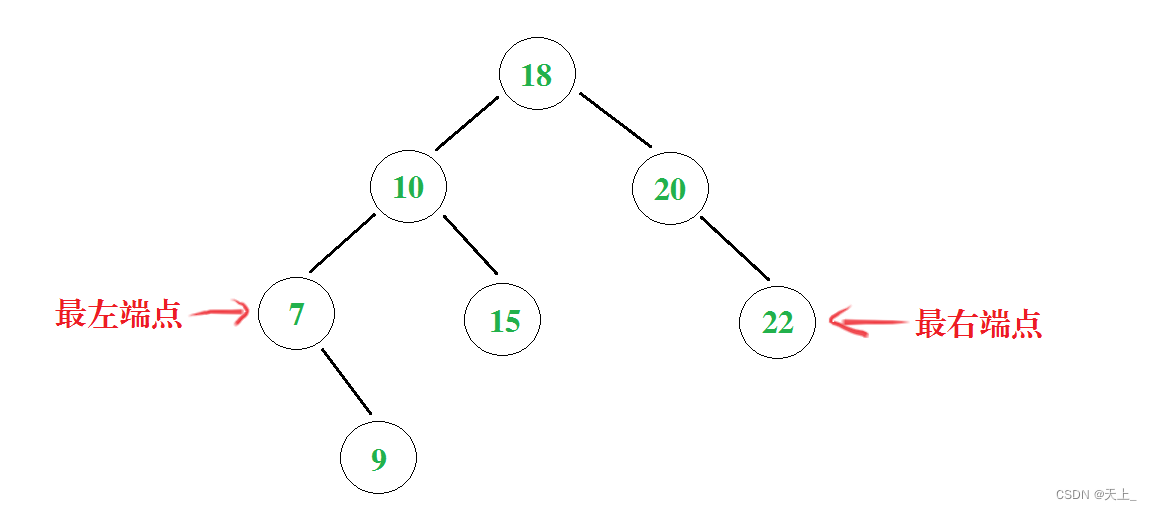
函数的代码实现也没什么难点，按照思路，在递归的方法实现中（查找最小元素）：节点的左子树不为空就进行递归，直到某一个节点的左子树为空就返回。

查找最小元素的递归函数

Position FindMin(BinTree BST)
{
	if (!BST)
	{
		return NULL;                  //空的二叉搜索树，返回NULL
	}
	else if (!BST->Left)
	{
		return BST;                   //找到最左的叶节点并返回
	}
	else
	{
		return FindMin(BST->Left);    //沿左分支继续查找
	}
}

在迭代的方法实现中：直接走到最左端或者最右端的节点即是最小元素或者最大元素。

查找最大元素的迭代函数 

Position FindMax(BinTree BST)
{
	if (BST)
	{
		while (BST->Right)
		{
			BST = BST->Right;  //沿右分支一直查找，直到最右叶节点
		}
	}
	return BST;
}

---

end

---

学习自：MOOC数据结构——陈越、何钦铭