一、Rational Arithmetic

（1）原题再现

Rational Arithmetic (20)__牛客网

For two rational numbers, your task is to implement the basic arithmetics, that is, to calculate their sum, difference,
product and quotient.

输入描述:

Each input file contains one test case, which gives in one line the two rational numbers in the format "a1/b1 a2/b2". 
The numerators and the denominators are all in the range of long int. If there is a negative sign, it must appear only in 
front of the numerator. The denominators are guaranteed to be non-zero numbers.

输出描述:

For each test case, print in 4 lines the sum, difference, product and quotient of the two rational numbers, respectively. The format of each 
line is "number1 operator number2 = result". Notice that all the rational numbers must be in their simplest form "k a/b", where k is 
the integer part, and a/b is the simplest fraction part. If the number is negative, it must be included in a pair of parentheses. If the 
denominator in the division is zero, output "Inf" as the result. It is guaranteed that all the output integers are in the range of long int.
输入
5/3 0/6
输出
1 2/3 + 0 = 1 2/3<br/>1 2/3 - 0 = 1 2/3<br/>1 2/3 * 0 = 0<br/>1 2/3 / 0 = Inf

（2）问题分析

对于两个有理数，你的任务是实现基本的算法，即计算它们的和、差，

乘积和商。

输入描述:

每个输入文件包含一个测试用例，在一行中给出两个有理数，格式为“a1/b1 a2/b2”。分子和分母都在长int的范围内。如果有负号，它必须只出现在分子前面。分母保证为非零数字。

输出描述:

对于每个测试用例，在4行中分别打印两个有理数的和、差、乘积和商。每个的格式第行是“number1运算符number2=结果”。注意，所有有理数都必须是最简单的形式“k a/b”，其中k是整数部分，而a/b是最简单的分数部分。如果数字是负数，则必须将其包含在一对圆括号中。如果除法中的分母为零，输出“Inf”作为结果。可以保证所有输出整数都在长整型的范围内。

（3）完整代码

import java.util.Scanner;

/*
 * 理性算数RationalArithmetic
 */

public class RationalArithmetic {
    public static void simplify(long a, long b) {
        long x = gcd(a, b);
        a /= x;
        b /= x;
        if (b < 0) {
            a *= -1;
            b *= -1;
        }
        if (a < 0) {
            if (-a % b == 0) {
                System.out.print("(" + a / b + ")");
            } else if (-a < b) {
                System.out.print("("+a + "/" + b+")");
            } else {
                System.out.print("(" + a / b + " " + (-a + (b * (a / b))) + "/" + b + ")");
            }
        } else {
            if (a % b == 0) {
                System.out.print(a / b);
            } else if (a < b) {
                System.out.print(a + "/" + b);
            } else {
                System.out.print(a / b + " " + (a - (b * (a / b))) + "/" + b );
            }
        }
    }
    public static long  gcd(long a, long b) { //辗转相除法求最大公约数
        if (b == 0) {
            return a;
        }
        long r = a % b;
        return gcd(b, r);
    }
    public static void add(long a, long b, long c, long d) {
        simplify(a, b);
        System.out.print(" + ");
        simplify(c, d);
        System.out.print(" = ");
        simplify(a * d + b * c, b * d);
    }
    public static void minus(long a, long b, long c, long d) {
        simplify(a, b);
        System.out.print(" - ");
        simplify(c, d);
        System.out.print(" = ");
        simplify(a * d - b * c, b * d);
    }
    public static void multiply(long a, long b, long c, long d) {
        simplify(a, b);
        System.out.print(" * ");
        simplify(c, d);
        System.out.print(" = ");
        simplify(a * c, b * d);
    }
    public static void division(long a, long b, long c, long d) {
        long m = a * d;
        long n = b * c;
        simplify(a, b);
        System.out.print(" / ");
        simplify(c, d);
        System.out.print(" = ");
        if (c == 0) {
            System.out.print("Inf");
        } else {
            if (n < 0) {
                m = m * -1; //把负号调整到分子上
                n = n * -1;
            }
            simplify(m, n);
        }
    }
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        while (sc.hasNext()) {
            String s = sc.nextLine();
            String[] split = s.split(" ");
            String[] s1 = split[0].split("/");
            String[] s2 = split[1].split("/");
            long a = Long.parseLong(s1[0]);
            long b = Long.parseLong(s1[1]);
            long c = Long.parseLong(s2[0]);
            long d = Long.parseLong(s2[1]);
            add(a, b, c, d);
            System.out.println();
            minus(a, b, c, d);
            System.out.println();
            multiply(a, b, c, d);
            System.out.println();
            division(a, b, c, d);
        }
    }
}

二、Pre-Post

（1）原题再现

Pre-Post__牛客网
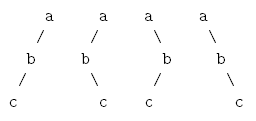
We are all familiar with pre-order, in-order and post-order traversals of binary trees. A common problem in data structure classes is to find the pre-order traversal of a binary tree when given the in-order and post-order traversals. Alternatively, you can find the post-order traversal when given the in-order and pre-order. However, in general you cannot determine the in-order traversal of a tree when given its pre-order and post-order traversals. Consider the four binary trees below:

All of these trees have the same pre-order and post-order traversals. This phenomenon is not restricted to binary trees, but holds for general m-ary trees as well.

输入描述:
Input will consist of multiple problem instances. Each instance will consist of a line of the form m s1 s2, indicating that the trees are m-ary trees, s1 is the pre-order traversal and s2 is the post-order traversal.All traversal strings will consist of lowercase alphabetic characters. For all input instances, 1 <= m <= 20 and the length of s1 and s2 will be between 1 and 26 inclusive. If the length of s1 is k (which is the same as the length of s2, of course), the first k letters of the alphabet will be used in the strings. An input line of 0 will terminate the input.
输出描述：
For each problem instance, you should output one line containing the number of possible trees which would result in the pre-order and post-order traversals for the instance. All output values will be within the range of a 32-bit signed integer. For each problem instance, you are guaranteed that there is at least one tree with the given pre-order and post-order traversals.
示例1
输入
2 abc cba
2 abc bca
10 abc bca
13 abejkcfghid jkebfghicda
输出
4
1
45
207352860
（2）问题分析

我们都熟悉二叉树的前序、中序和后序遍历。数据结构类中的一个常见问题是，当给定二叉树的中序遍历和后序遍历时，如何找到二叉树的前序遍历。或者，您可以在给定内序和前序时找到后序遍历。然而，当给定树的前序遍历和后序遍历时，通常无法确定树的序遍历。考虑下面的四棵二叉树:

所有这些树都有相同的前序和后序遍历。这种现象并不局限于二叉树，也适用于一般的m-ary树。

输入描述:
输入将由多个问题实例组成。每个实例将由m s1 s2形式的一行组成，表示树是m-ary树，s1是前序遍历，s2是后序遍历。所有遍历字符串将由小写字母字符组成。对于所有输入实例，1 <= m <= 20, s1和s2的长度将介于1到26之间。如果s1的长度是k(当然与s2的长度相同)，字母表的前k个字母将被用于字符串中。输入行为0将终止输入。
输出描述:
对于每个问题实例，您应该输出一行，其中包含可能的树的数量，这将导致实例的前序和后序遍历。所有输出值都将在32位有符号整数的范围内。对于每个问题实例，保证至少有一棵树具有给定的前序和后序遍历。

（3）完整代码
/*
 * 前柱Pre-Post
 */
import java.util.*;
class SubTree {
    public SubTree(String pre, String post) {
        this.pre = pre;
        this.post = post;
    }
    String pre;
    String post;
}
public class Main {
    //计算阶乘
    public static  long fac(int n) {
        long f = 1;
        for (int i = 1; i <= n; i++) {
            f *= i;
        }
        return f;
    }
    //计算C n m
    public static long calcCom(int n, int m) {
        m = m < (n - m) ? m : (n - m);
        long r = 1;
        for (int i = n; i >= n - m + 1; i--) {
            r *= i;
        }
        return r / fac(m);
    }
    public static List<SubTree> calcSubTree(String prev, String post) {
        //子树的根在前序遍历结果中的位置
        int subRootPreIdx = 1;
        //后序遍历
        int postFirst = 0;
        List<SubTree> subTreeList = new ArrayList<>();
        while (subRootPreIdx < prev.length()) {
            //确认该棵子树的根节点
            char rootSub = prev.charAt(subRootPreIdx);
            int subRootPostIdx = post.indexOf(rootSub);
            int subTreeNodeCount = subRootPostIdx - postFirst + 1;
            //从前序和后续遍历结果中分离出该棵子树的前序和后序遍历结果
            SubTree subTree = new SubTree(
                prev.substring(subRootPreIdx, subRootPreIdx + subTreeNodeCount),
                post.substring(postFirst, postFirst + subTreeNodeCount)
            );
            subTreeList.add(subTree);
            //继续分离下一棵子树
            subRootPreIdx += subTreeNodeCount;
            postFirst += subTreeNodeCount;
        }
        return subTreeList;
    }
    public static long CalcTreePossible(int m, String pre, String post) {
        if (pre.isEmpty() || pre.length() == 1) {
            return 1;
        }
        //先分离出根节点有多少棵树
        List<SubTree> subTree =  calcSubTree(pre, post);
        //根节点子树可能性的组合结果
        long result = calcCom(m, subTree.size());
        //根的子树有多少种可能性
        for (SubTree e : subTree) {
            result *= CalcTreePossible(m, e.pre, e.post);
        }
        return result;
    }
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        while (in.hasNext()) {
            int m = in.nextInt();
            if (m == 0) {
                break;
            }
            //接收子树的前序和后续遍历结果
            String pre = in.next();
            String post = in.next();

            System.out.println(CalcTreePossible(m, pre, post));
        }
    }
}