整型数据类型

在上一节当中，我们遇到了用int关键词（整数integer的缩写）来表示一个整数的数据类型。
这一节中，我们来详细讨论一下C语言里面的整数数据类型。

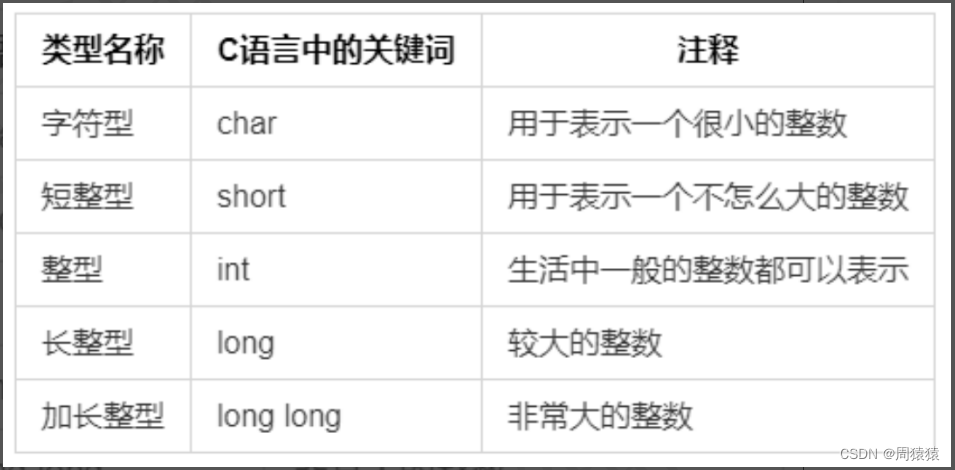
在C语言中，有上面表中列出的几种整型数据类型。
看到这里你可能想问，一个整数而已，为什么会需要定义这么多不同的类型出来呢？
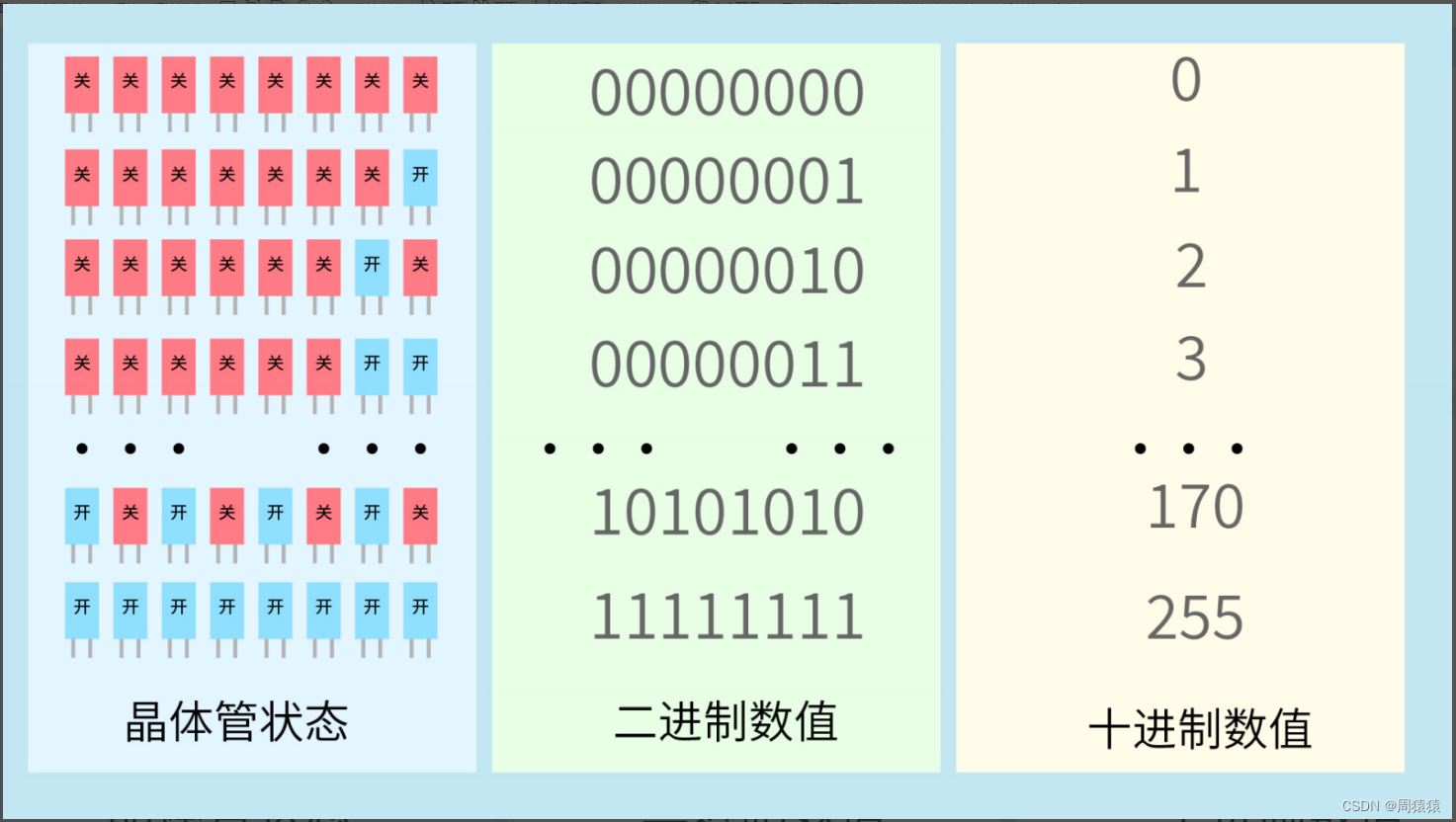
计算机通过晶体管的开关状态来记录数据。它们通常8个编为一组，我们称之为字节。而晶体管有开关
两种状态，一个字节有8个晶体管，因此一个字节可以拥有2的八次方个不同的状态。让每一种状态对应
一个数值，这样一个字节可以表示256个不同数值。

要表示更大的数据范围就需要更多晶体管。要知道在发明C语言的年代，计算机存储资源是非常珍贵而
稀缺的。对存储资源，程序员可能恨不得把一块掰成两块来用。如果只想表达0到100以内的数值，那么
一个字节就足够了，何必用两个字节来存储呢？
而如今，即使存储资源已经较为丰富了，但是大部分的强类型语言，都延续了这个传统。它们均提供了
丰富的类型以供选用。而程序员在编写代码时，通常能预想到需要使用到的数据范围的大小。这样在处
理一个数据时，可以从语言所提供的类型中选用最合适的类型来承载数据。
那么接下来，你可能想知道这些类型中，它们分别占用几个字节，具体的数据范围是多少？从而合适地
选择数据类型。很遗憾，我不能准确地告诉大家。因为C语言标准并未规定这些数据类型的大小范围，
具体的实现交由了编译器和平台决定。那我们怎样知道在visual studio 2019中，各种整型数据类型能够
表示的数据范围呢？
我们需要sizeof关键词来帮我们测量。

用sizeof关键词来测量大小

和int一样，sizeof是C语言中的一个关键词。它是英文size of连起来的合成词。翻译成中文就是什么东西
的大小的意思。它能够测量C语言各种实体所占用的字节大小。
如果我们想看int所占用的字节大小，可以这样写sizeof(int)。执行后这段代码后，它的测量结果是一个
整型。我们可以借助printf函数将测量结果显示在控制台上。我们现在可以假设sizeof返回的结果是int类型的，在printf函数中使用占位符%d。而更准确的用法，应该用%zu。
测量int类型所占用的字节大小，并将结果打印在控制台上的代码如下：

printf("%d\n", sizeof(int));

sizeof后面既可以跟类型，也可以跟变量、常量。
1. 跟类型，测类型所占用字节的大小。
2. 跟变量，测变量的类型所占用字节大小。
3. 跟常量，测常量的类型所占用字节大小。
下面是以上三种情况的示例代码。

int a;
printf("sizeof int = %d\n", sizeof(int)); // 1.测类型所占用字节的大小
printf("sizeof a = %d\n", sizeof(a)); // 1.测变量的类型所占用字节大小
printf("sizeof 123 = %d\n", sizeof(123)); // 1.测常量的类型所占用字节大小

现在我们可以在自己的电脑上运行一下，看看C语言中提供的各种整型类型的大小。

printf("sizeof char=%d\n", sizeof(char));
printf("sizeof short=%d\n", sizeof(short));
printf("sizeof int=%d\n", sizeof(int));
printf("sizeof long=%d\n", sizeof(long));
printf("sizeof long long=%d\n", sizeof(long long));

运行一下，我们看到了结果。
char，short，int，long，long long分别占用了1，2，4，4，8个字节。至此，我们已经得知了它们所占
字节大小，并且验证了可以表示越大范围的数据类型所占用的字节越多。
值得注意的是在Visual Studio 2019中，int和long均占用4个字节。这并未违反C语言标准，C语言标准规
定高级别的类型取值范围不得小于低级别的类型，但是它们可以是一致的。
下面我们继续讨论一下，各种类型它们所能表达的数值范围具体是多少。

三位二进制表示的数值范围

TIPS:
如果暂时无法理解关于整型表达范围的原理分析，请先记住sizeof的使用和各种整型变量的表达范围的
结论即可。不理解整型表达范围的原理不影响对C语言的使用。
char，short，int，long，long long分别占用了1，2，4，4，8个字节。而每个字节由8个晶体管组成，
每个晶体管状态我们称之为位。那么char，short，int，long，long long分别占用了8，16，32，32，64
位。
太多的位不利于我们理解原理，我们暂时把问题简化一下，试试看位数减少到3。然后，分析3位的组
合，它能表示多大范围的数值呢？

三位二进制组成的数据类型，可以表达2的3次方也就是8个数值。如果从0开始，那么可以表达从0到7的
数据范围。那么我们可以得出以下结论：
如果不考虑负数，那么整型数据类型可以表达的数据范围是：
假设，位数为n，则数据范围从【0】开始，到【2的n次方-1】的数值范围。
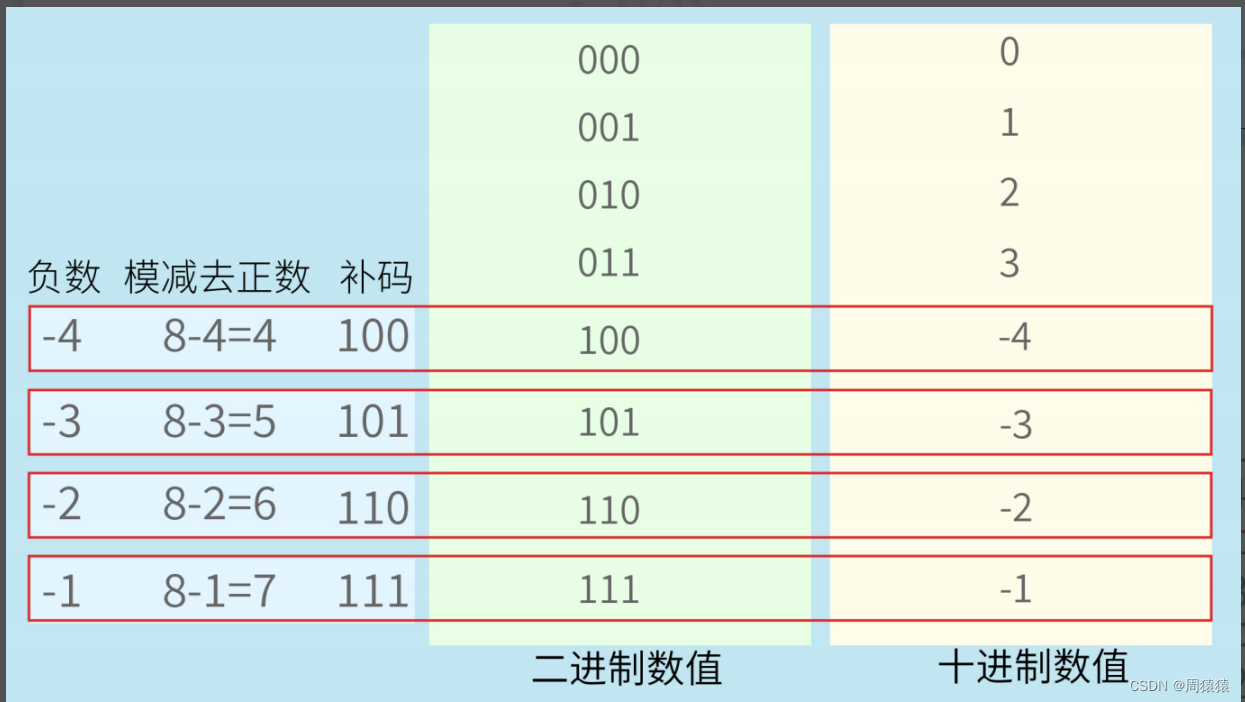
对的，你肯定意识到了，负数怎么办？那我们需要拿出一个位来作为符号位。用来表示这个数据是正数
还是负数。在IEEE标准中，这个符号位存在于二进制的最高位。让我们用三位二进制来示范这种情况。

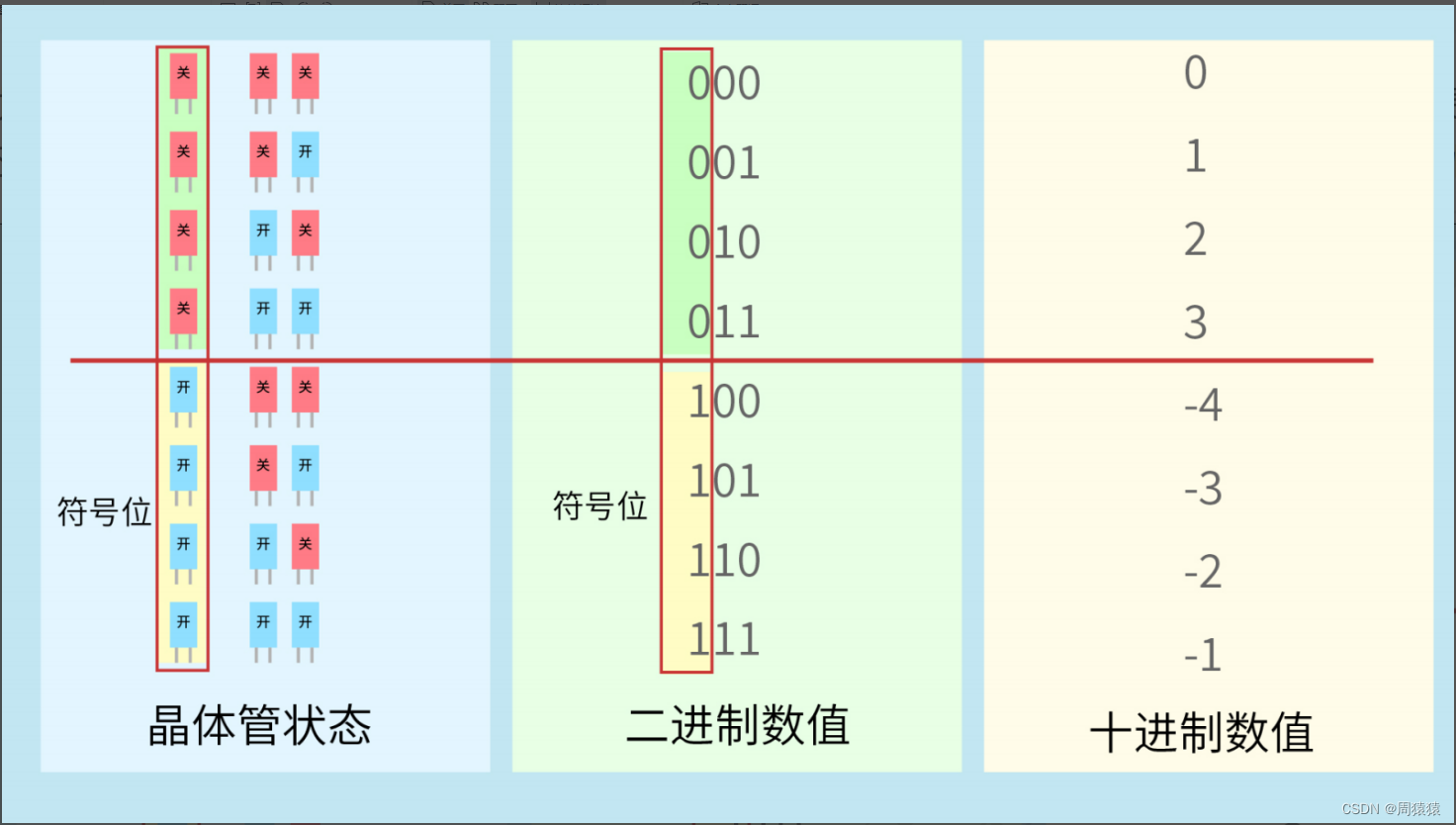
加上符号之后，现在取值范围变为负4到3了。红框中的为最高位，最高位为1的表示负数。你可能会觉
得有点奇怪，为什么3的二进制是011，而负3却是101呢？如果简单的加一个符号位，为什么不用111
呢？那我们看看如图中所示的3与负3相加的运算结果。

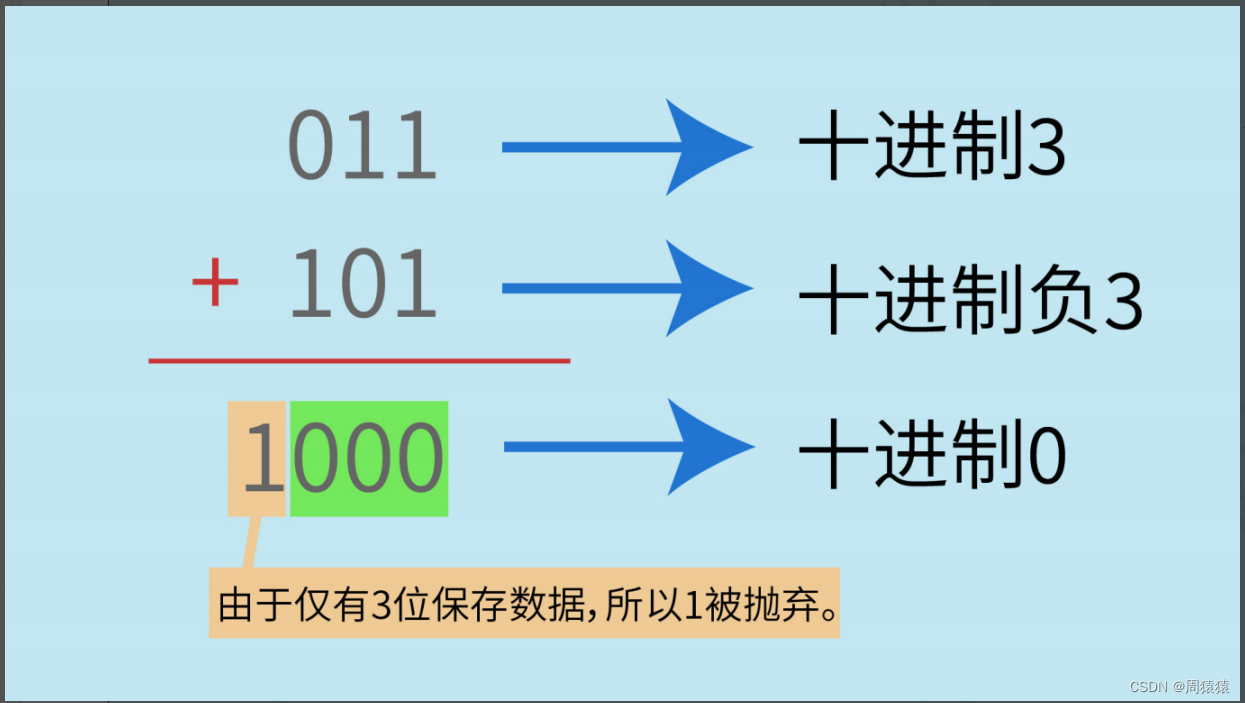
你会惊奇地发现，用101来表示负3与用011表示的正3相加。结果为1000，但是由于仅有3位二进制来保
存数据，最高位1被丢弃了。结果为000，居然得到了正确的结果0。为什么会这样呢？

数值的补码表示法

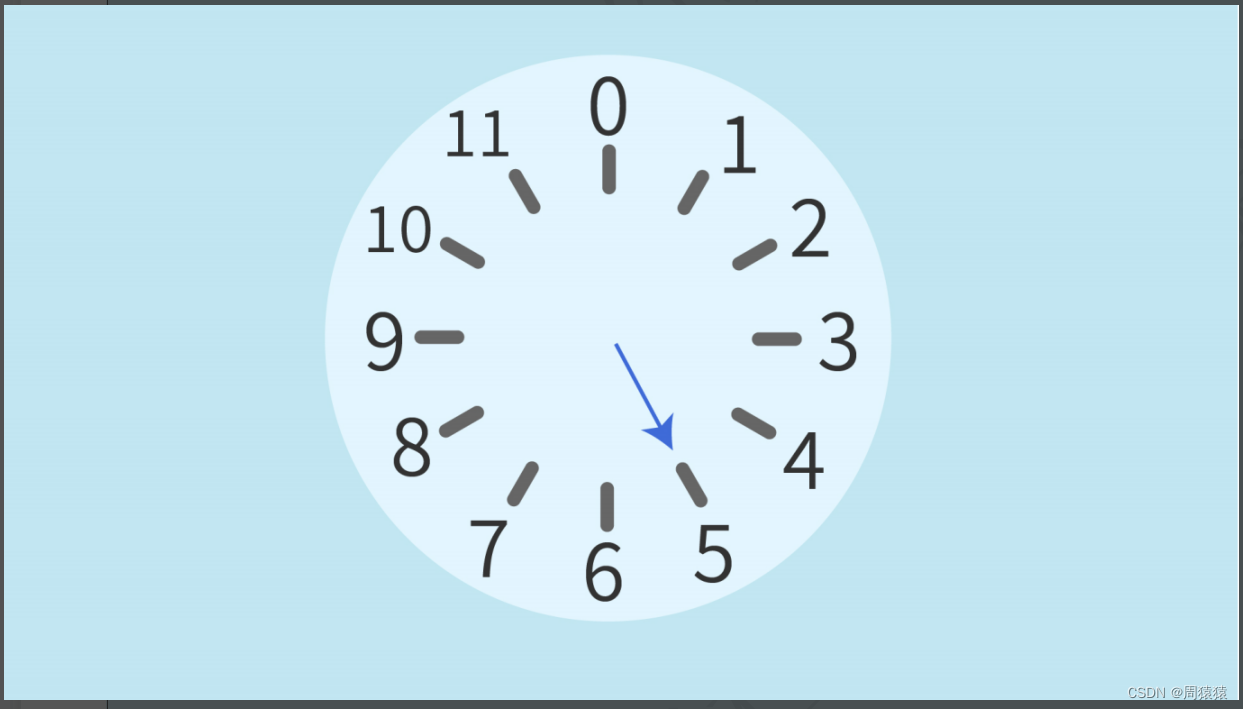
我们来观察上图的时钟，这个时钟是一个圆被分成了12个点，让我们假设这个时钟一步只能走一个整
点。那么这个时钟只有12种不同的模式，我们把12称之为时钟的模。
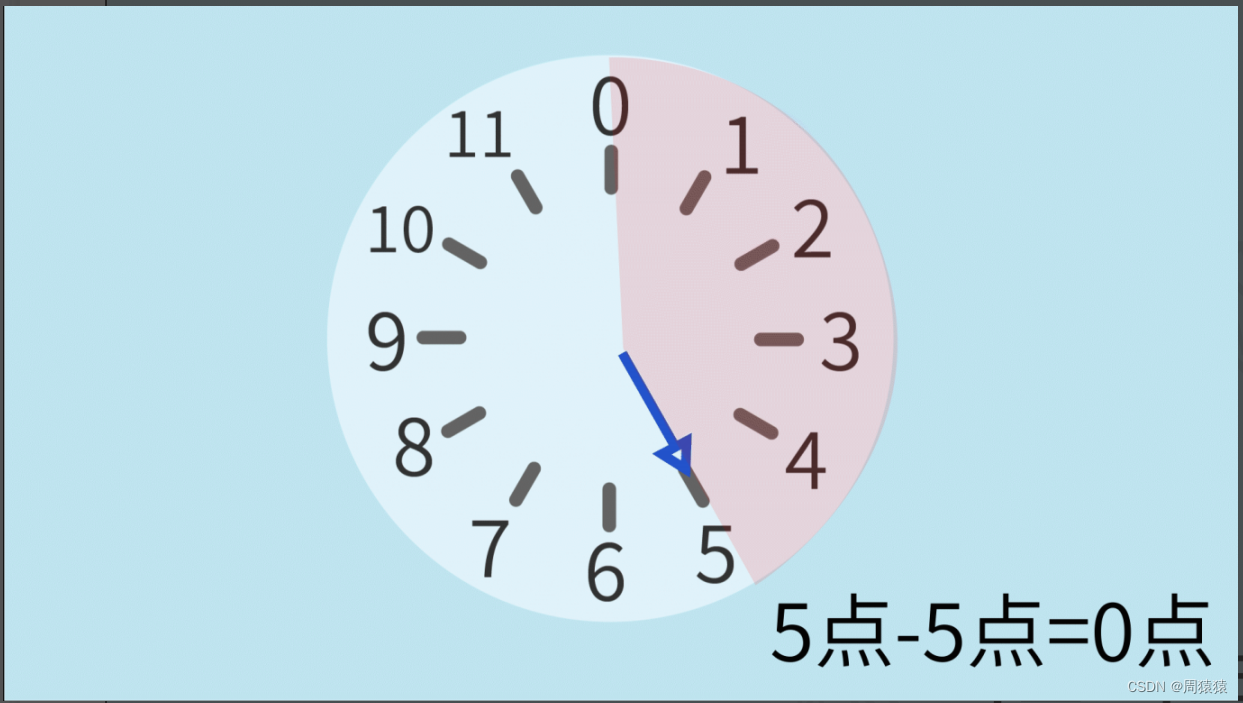
现在指针指向了5点，我们要让指针回到0点。一个办法是直接回退5个小时（5-5）。

另一个办法是继续往前走7个小时（5+7）。

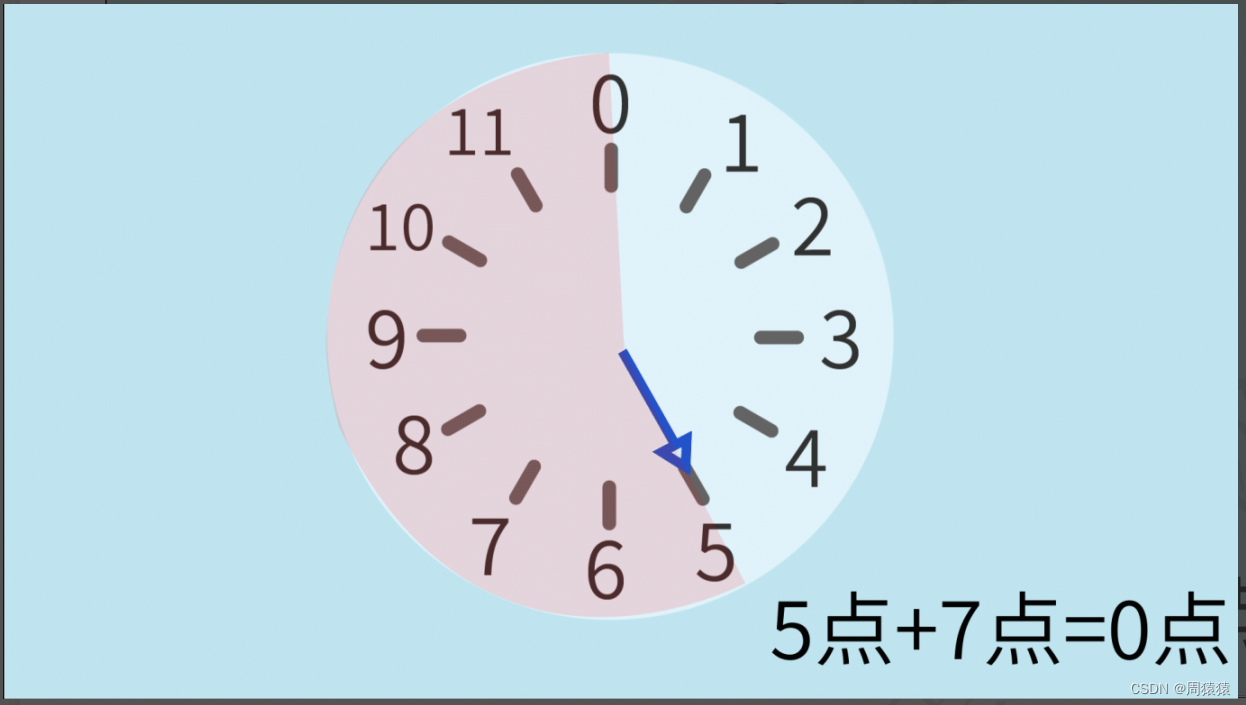
在第二种办法中，5+7=12，而12刚好为时钟的模，时钟指向12的同时，也正好指向了0。
要让指针回到0点，只需要让它加上模与当前的时间的差即可。
因此，指针回退5小时与指针前进7小时是等价的。我们可以用指针前进来代替指针后退。
让我们将这种思想带入到上面讨论的三位二进制当中。三位二进制能表示8中不同的模式，因此它的模
为8。要让3回到0，我们可以让3减去3，也可以让3加上模与3的差，即8-3=5。因此，我们可以把-3在三
位二进制中用5的二进制101表示。
这种将用加法来等效减法的二进制表示法被称之为补码表示法。
正数的补码就是其二进制本身。
而正数对应的负数的补码为：(模 - 正数)的二进制。

补码表示法既通过最高位，区别了正数和负数。并且，巧妙地应用了溢出，所得到的计算结果也是正确
的。类似于钟表仅需要向前走就可以实现减法，计算机的电路设计中，也只需要设计加法电路。极大地
简化了计算机内部电路的复杂程度。
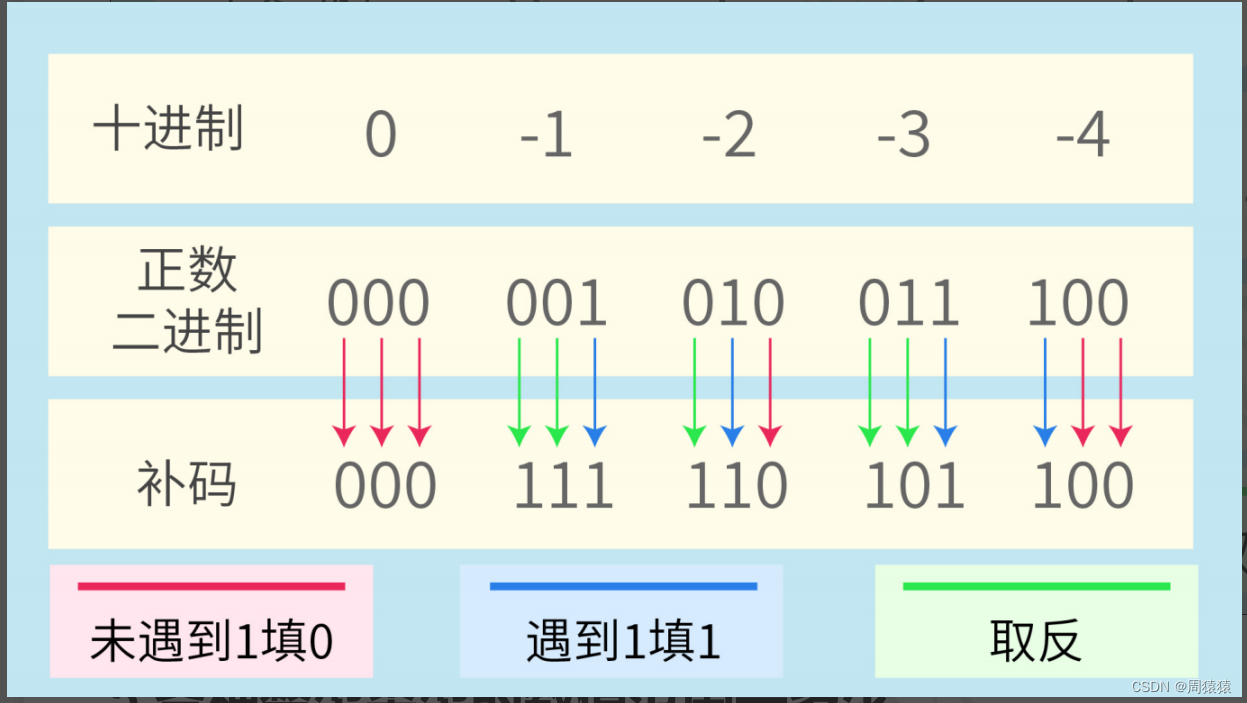
求一个正数对应的负数的补码的第二种办法：
1. 先写出这个正数的二进制。
2. 从二进制的右边开始，遇到第一个1之前，全都填0。
3. 遇到第一个1之后，把1填下来。
4. 1之后的全部取反。

各种整型类型的数值范围是多少

终于可以回到最前面的问题了。各种整型变量的数值范围是多少？

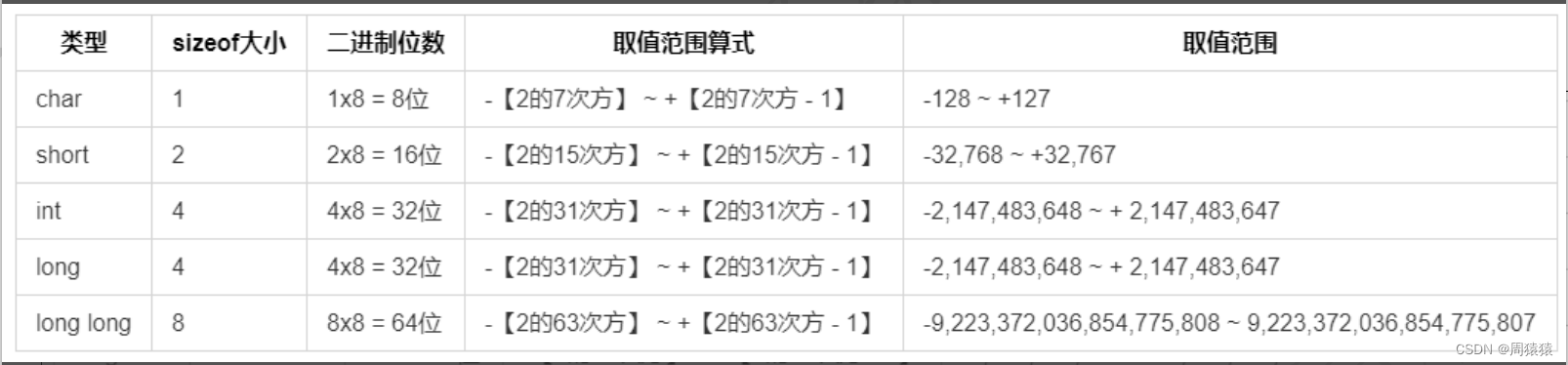
次方数比位数少一，是因为最高位被用去做符号位了。

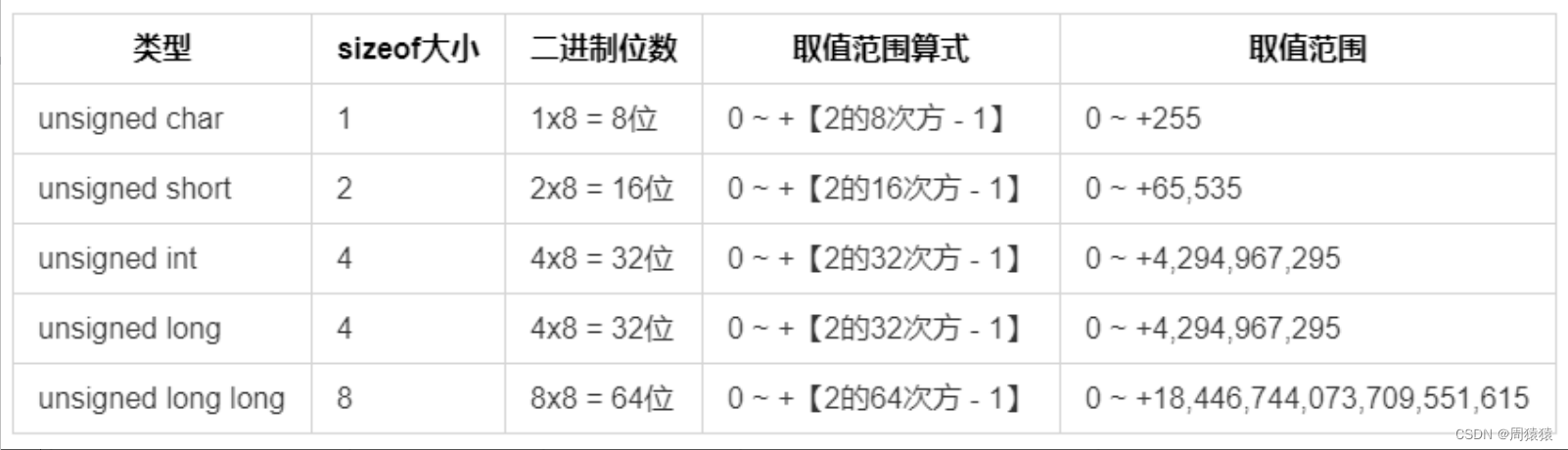
无符号整型

如果你确定你不会用到负数，那么请使用unsigned关键词。表明这个数据类型，是不带有符号位的。既
然不带有符号位了，那么原本留给符号位的那一个二进制位，可以用来表示数值。