基本概念
连通:若a->b存在路径,即为连通
连通图:该图中任意两点均连通,即为连通图
连通分量:下图为无向图,但存在三个连通分量
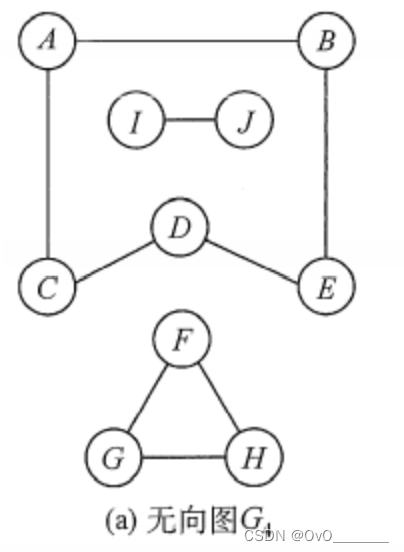
强连通图:双向的连通图
强连通分量:有向图中的双向连通
图的存储结构
邻接矩阵:顺序存储,二维数组耗费大量空间
原理:有路径flag=1,flag=0;
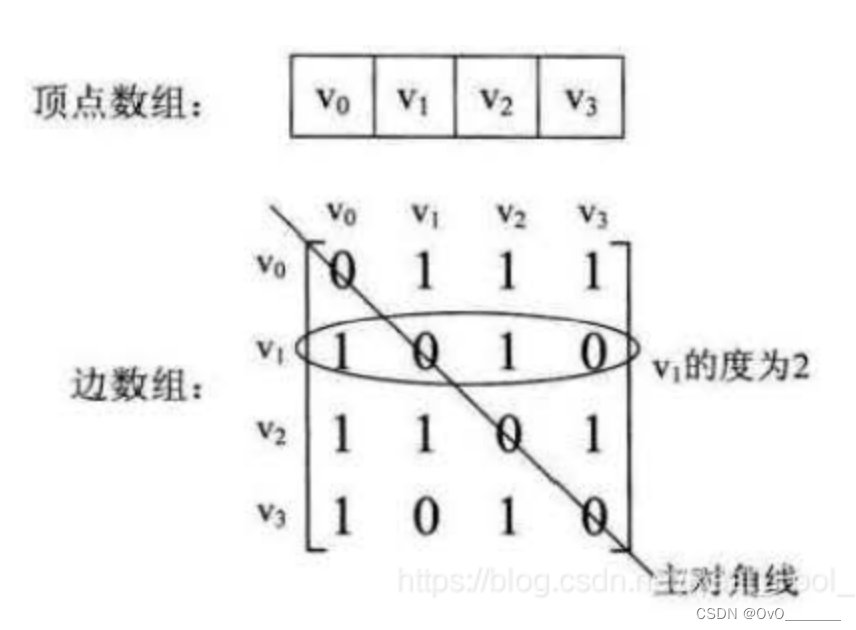
①无向图中为对称矩阵
②有向图中A [ i ] [ j ],i->j 或 j->i
邻接表:链式存储+顺序存储
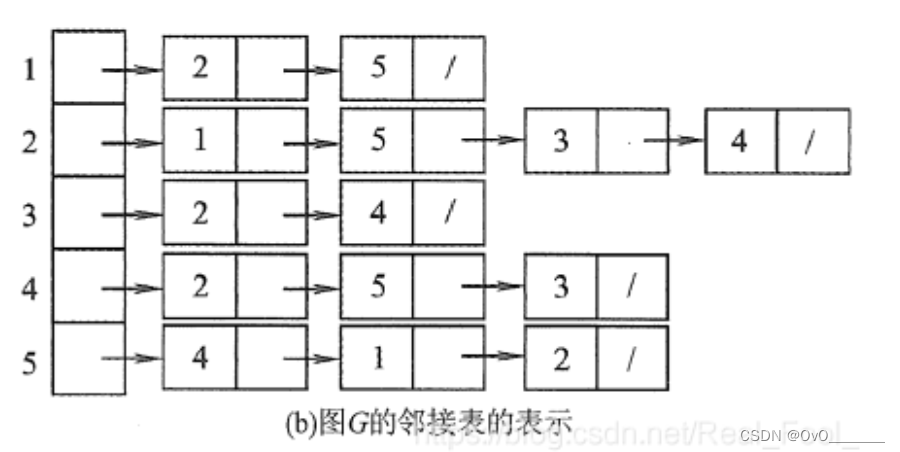
图的遍历
DFS
1.变量设置:
map【】【】地图数组
book【】【】标记数组
dx【】,dy【】方向数组
2.终止条件
3.核心:
标记
递归dfs
回溯(取消标记)
#include<stdio.h>
int a[110][110]; //地图,0为通路,1为障碍物
int book[110][110]; //标记数组
int minn=999999,step;
int hx,hy; //终点
int min(int a,int b)
{
return a<b?a:b;
}
void dfs(int x,int y,int step)
{
//方向数组
int dx[4]= {1,-1,0,0};
int dy[4]= {0,0,1,-1};
int tx,ty;
//终止条件
if(hx==x&&y==hy)
{
minn=min(minn,step);
return ; //回溯
}
for(int i=1; i<=4; i++)
{
int tx=x+dx[i];
int ty=y+dy[i];
if((a[tx][ty]==0)&&(book[tx][ty]==0))
{
book[tx][ty]=1; //已走标记
dfs(tx,ty,step+1);
book[tx][ty]=0; //取消标记
}
}
return ;
}
int main()
{
int n,m;
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
scanf("%d",&a[i][j]);
}
dfs(sx,sy); //起点
printf("%d",step);
} BFS
1.结构体,x,y,step
2.首先起点入队,队首向四周扩展并将点(队尾)入队,直到不能扩展则队首出队,此时队尾变为队首,重复上述操作
#include<bits/stdc++.h>
using namespace std;
int a[100][100],v[100][100];
struct point
{
int x;
int y;
int step;
};
queue<point> r;
int dx[4]={0,1,0,-1};
int dy[4]={1,0,-1,0};
int main()
{
//输入
int n , m ,startx,starty,p,q;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
scanf("%d",&a[i][j]);
scanf("%d%d%d%d",&startx,&starty,&p,&q);
//BFS
point start;
start.x=startx;
start.y=starty;
start.step=0;
r.push(start);//将起点入队
v[startx][starty]=1;
int flag=0;
while(!r.empty())
{
int x=r.front().x,y=r.front().y;
if(x==p&&y==q)
{
flag=1;
printf("%d",r.front().step);
break;
}
for(int k=0;k<=3;k++)
{
int tx,ty;
tx=x+dx[k];
ty=y+dy[k];
if(a[tx][ty]==1&&v[tx][ty]==0)
{
//入队
point temp;
temp.x=tx;
temp.y=ty;
temp.step=r.front().step+1;
r.push(temp);
v[tx][ty]=1;
}
}
r.pop();//队首出队
}
if(flag==0)
printf("no answer!");
return 0;
}
/*
5 4
1 1 2 1
1 1 1 1
1 1 2 1
1 2 1 1
1 1 1 2
1 1 4 3
*/
最小生成树
原理:
生成树:一个连通图的生成树是一个极小的连通子图,n个结点n-1条边;
最小生成树:边的权值之和最小的生成树,即从a->b的最短
若多一条边,则会构成回路(双向),若少一条边,则会缺一条路径;
算法实现:
Prim算法(稠密图)
从某一个单独结点开始,每次找权值最小的边,并连接其后继结点,构成整个最小生成树(n点n-1边)
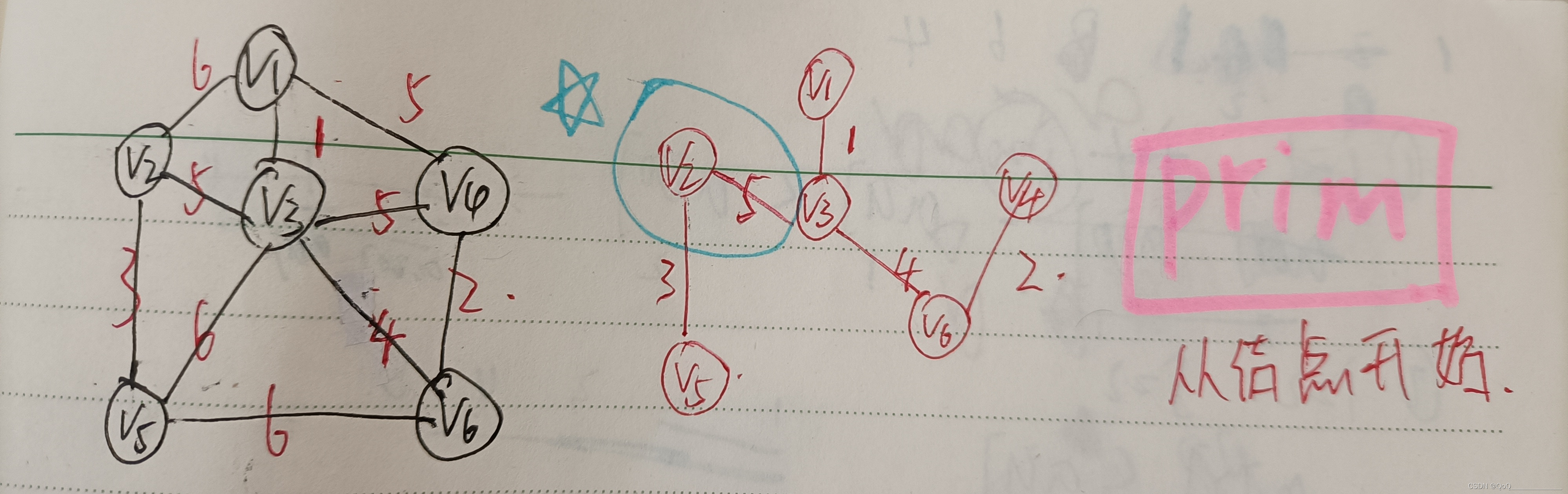
#include <stdio.h>
#include <string.h>
#define INF 0x3f3f3f3f //无穷大
int n, m,a[1001][1001], dis[100001], ans;
int book[100001];
int main()
{
memset(dis, INF, sizeof(dis)); //初始化dis【】大值
dis[1] = 0; //起点自己到自己距离为0
scanf("%d %d", &n,&m);
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= n; j++)
{
scanf("%d", &a[i][j]); //二维数组存图,i->j
}
}
for(int i = 1; i <= n; i++)
{
int t = 0;
for(int j = 1; j <= n; j++)
{
if(!book[j] && dis[j] < dis[t]) //寻找未标记且权值最短边(类似kruskal找最小边)
{
t = j; //记录最短边的终点t
}
}
book[t] = 1; //标记,代表已加入最小生成树
for(int j = 1; j <= n; j++)
{
if(!book[j] && a[t][j] < dis[j]) //更新最短距离
{
dis[j] = a[t][j];
}
}
}
for(int i = 1; i <= n; i++)
{
ans +=dis[i]; //把所有在最小生成树中的点的权值加起来
}
printf("%d", ans);
return 0;
}
Kruskal算法(稀疏图)
从最小的边开始找,并连接最小边的两个结点,直到整个图形成最小生成树(n点n-1边)
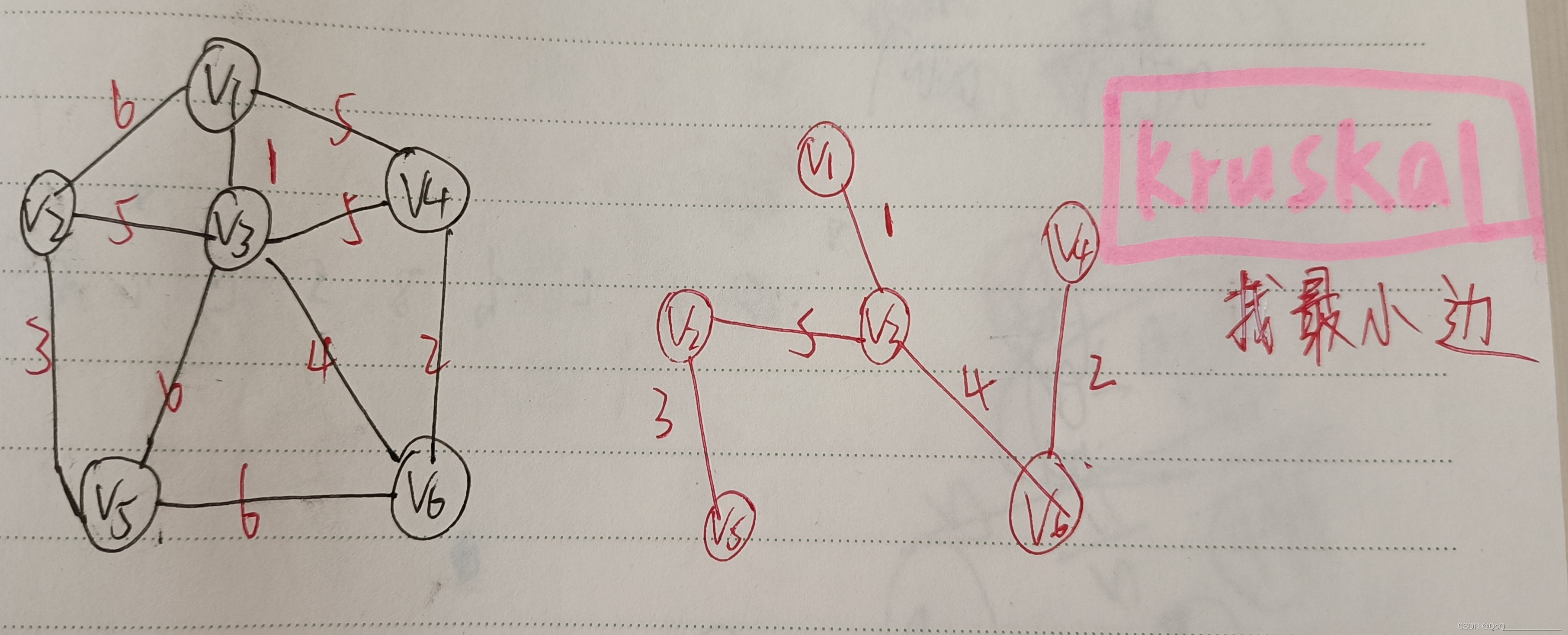
#include<stdio.h>
#include<stdlib.h>
int n,m;
long long sum;
int fa[200005];
int cnt=0;
struct node
{
int x;
int y;
int z;
} a[200005];
void init(int n)
{
for(int i = 1; i <= n; i++)
{
fa[i] = i;
}
}
int find(int x)
{
if(x==fa[x])
return x;
else
return find(fa[x]);
}
int cmp(const void*a,const void*b)
{
struct node aa=*(struct node*)a;
struct node bb=*(struct node*)b;
return aa.z>bb.z?1:-1; //升序
//降序:return aa.z>bb.z?-1:1;
}
int main()
{
int v,k=0;
scanf("%d", &n);
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= n; j++)
{
scanf("%d", &v);
if(j > i) //无向存图
{
k++;
a[k].x = i;
a[k].y = j;
a[k].z = v;
}
}
}
qsort(a + 1, a + k + 1, sizeof(a[1]),cmp);//排序函数
for(int i = 1; i <= m; i++)
{
int x=find(a[i].x);
int y=find(a[i].y);
if(x!=y) //合并
{
f[y]=x;
sum+=a[i].z; //权值相加
cnt++;
}
if(cnt==n-1) //n个点,n-1条边,边用完跳出循环
break;
}
printf("lld\n",sum);
return 0;
}
0
最短路径
从a->b的权值最小的一条路径
多源Floyed
原理:利用三重循环,实时更新最短路径;
1.含义:
a【i】【j】:i--j 直接距离
a【i】【k】+ a【k】【j】:i--j 间接距离(经过k中转站)
2.解释:
求 i--j 的最短路径则讨论 i--j,i--1站点--j,i-2站点--j,i--3站点--j... ...
依次枚举比大小,实时更新


单源Dijkstra

int dijk(int from,int to) //单源点到目标点
{
int dis[N]; //距离数组
int book[N]; //标记数组
int map[N][N]; //存储两点间距离
int pos; //每次最短路径的站点
//book[from]=1; //标记起点
//初始化
memset(book,0,sizeof(book));
for(int i=1; i<=n; i++)
{
dis[i]=map[from][i]; //最初单源点到目标点的直达的距离,无中转站
}
//每次找最小边,连接其两点
for(int i=1; i<=n; i++) //遍历1-n个站点
{
int min=INF;
for(int j=1; j<=n; j++)
{
if(min>dis[j]) //每次找最小边的对应点pos
{
min=dis[j];
pos=j;
}
}
book[pos]=1; //找到并标记该点pos
for(int k=1; k<=n; k++) //列举从1-n的站点,到达pos点的最短路径
{
if((dis[pos]>dis[k]+map[k][pos])&&!book[k])
{
dis[pos]=dis[k]+map[k][pos];
}
}
}
return dis[to]; //所有站点的dis【】已经标记,找需求to即可
}