word2vec 的机制中的 CBOW 模型。因为 CBOW 模型是一个简单的 2 层神经网络，所以实现起来比较简单。但是，目前的实现存在几个问题，其中最大的问题是，随着语料库中处理的词汇量的增加，计算量也随之增加。实际上，当词汇量达到一定程度之后，上一章的 CBOW 模型的计算就会花费过多的时间。

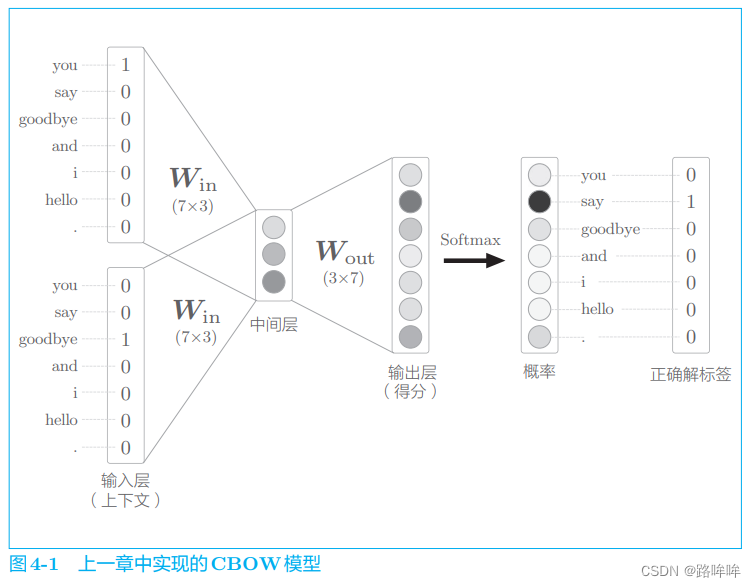
如图 4-1 所示，上一章的 CBOW 模型接收拥有 2 个单词的上下文，并基于它们预测 1 个单词（目标词）。此时，通过输入层和输入侧权重（$W_{in}$） 之间的矩阵乘积计算中间层，通过中间层和输出侧权重（$W_{out}$）之间的矩阵乘积计算每个单词的得分。这些得分经过 $Softmax$ 函数转化后，得到每个单词的出现概率。通过将这些概率与正确解标签进行比较（更确切地说，使用交叉熵误差函数），从而计算出损失。

图 4-1 中的 CBOW 模型在处理小型语料库时问题不大。不过在处理大规模语料库时，这个模型就存在多个问题了。为了指出这些问题，这里我们考虑一个例子。假设词汇量有 100 万个，CBOW 模型的中间层神经元有 100 个， 此时 word2vec 进行的处理如图 4-2 所示。

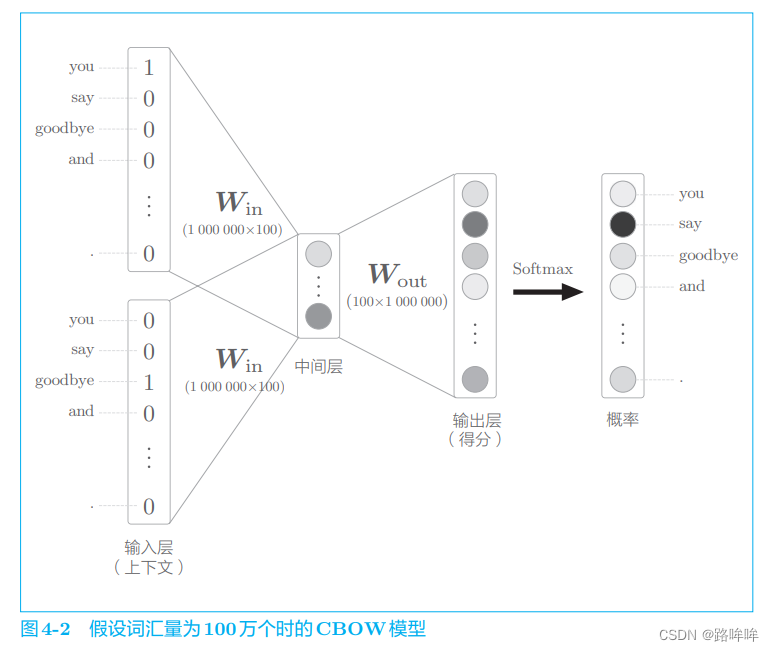
如图 4-2 所示，输入层和输出层存在 100 万个神经元。在如此多的神经元的情况下，中间的计算过程需要很长时间。具体来说，以下两个地方的计算会出现瓶颈。

• 输入层的 $one-hot$ 表示和权重矩阵 $W_{in}$ 的乘积

• 中间层和权重矩阵 $W_{out}$ 的乘积以及 $Softmax$ 层的计算

第 1 个问题与输入层的 $one-hot$ 表示有关。这是因为我们用 $one-hot$ 表示来处理单词，随着词汇量的增加，$one-hot$ 表示的向量大小也会增加。比如，在词汇量有 100 万个的情况下，仅 $one-hot$ 表示本身就需要占用 100 万个元素的内存大小。此外，还需要计算 $one-hot$ 表示和权重矩阵 $W_{in}$ 的乘 积，这也要花费大量的计算资源。

第 2 个问题是中间层之后的计算。首先，中间层和权重矩阵 $W_{out}$ 的乘积需要大量的计算。其次，随着词汇量的增加，$Softmax$ 层的计算量也会增加。

4.1 word2vec 的改进①

4.1.1 Embedding 层

在上一章的 word2vec 实现中，我们将单词转化为了 $one-hot$ 表示，并将其输入了 $MatMul$ 层，在 $MatMul$ 层中计算了该 $one-hot$ 表示和权重矩阵的乘积。这里，我们来考虑词汇量是 100 万个的情况。假设中间层的神经元个数是 100，则 MatMul 层中的矩阵乘积可画成图 4-3。

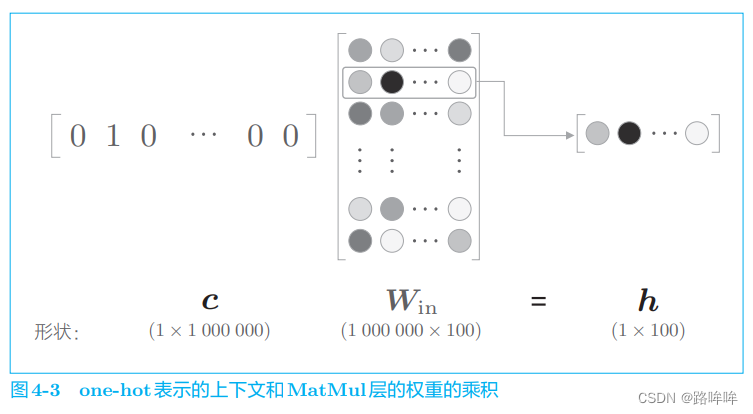
如图 4-3 所示，如果语料库的词汇量有 100 万个，则单词的 $one-hot$ 表示的维数也会是 100 万，我们需要计算这个巨大向量和权重矩阵的乘积。但是，图 4-3 中所做的无非是将矩阵的某个特定的行取出来。因此，直觉上将单词转化为 $one-hot$ 向量的处理和 $MatMul$ 层中的矩阵乘法似乎没有必要。

现在，我们创建一个从权重参数中抽取 “单词 ID 对应行（向量）” 的层，这里我们称之为 Embedding 层。

在自然语言处理领域，单词的密集向量表示称为词嵌入（word embedding）或者单词的分布式表示（distributed representation）。 过 去，将基于计数的方法获得的单词向量称为 distributional representation，将使用神经网络的基于推理的方法获得的单词向量称为 distributed representation。不过，中文里二者都译为 “分布式表示”。

4.1.2 Embedding 层的实现

见书（后续再补充）

4.2 word2vec 的改进②

如前所述，word2vec 的另一个瓶颈在于中间层之后的处理，即矩阵乘积和 Softmax 层的计算。本节的目标就是解决这个瓶颈。这里，我们将采用名为负采样（negative sampling） 的方法作为解决方案。使用 Negative Sampling 替代 Softmax，无论词汇量有多大，都可以使计算量保持较低或恒定。

4.2.1 中间层之后的计算问题

为了指出中间层之后的计算问题，和上一节一样，我们来考虑词汇量为 100 万个、中间层的神经元个数为 100 个的 wod2vec（CBOW 模型）。此时， word2vec 进行的处理如图 4-6 所示。

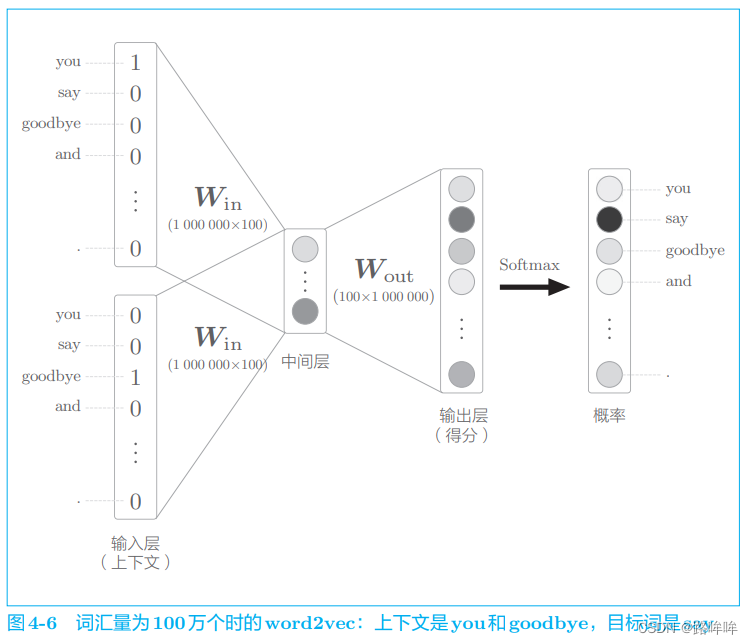
如图 4-6 所示，输入层和输出层有 100 万个神经元。在上一节中，通过引入 Embedding 层，节省了输入层中不必要的计算。剩下的问题就是中间层之后的处理。此时，在以下两个地方需要很多计算时间。

• 中间层的神经元和权重矩阵（$W_{out}$）的乘积
• Softmax 层的计算

第 1 个问题在于巨大的矩阵乘积计算。在上面的例子中，中间层向量的大小是 100，权重矩阵的大小是 100 × 1 000 000 万，如此巨大的矩阵乘积计算需要大量时间（也需要大量内存）。此外，因为反向传播时也要进行同样的计算，所以很有必要将矩阵乘积计算“轻量化”。

其次，Softmax 也会发生同样的问题。换句话说，随着词汇量的增加，Softmax 的计算量也会增加。观察 Softmax 的公式，就可以清楚地看出这一点。下面是 Softmax 的计算公式：
$$y_k=\frac{exp(s_k)}{{\sum }_{i=1}^{1000000}exp(s_i)}$$
式 (4.1) 是第 k 个元素（单词）的 Softmax 的计算式（各个元素的得分 为 $s_1$, $s_2$, ···）。因为假定词汇量是 100 万个，所以式 (4.1) 的分母需要进行 100 万次的 exp 计算。这个计算也与词汇量成正比，因此，需要一个可以替 代 Softmax 的“轻量”的计算。

4.2.2 从多分类到二分类

对于负采样，这个方法的关键思想在于二分类 （binary classification），更准确地说，是用二分类拟合多分类（multiclass classification），这是理解负采样的重点。

到目前为止，我们已经做到了当给定上下文时，以较高的概率预测出作为正确解的单词。比如，当给定 you 和 goodbye 时，使神经网络预测出单词 say 的概率最高。如果学习进展顺利，神经网络就可以进行正确的预测。

现在，我们来考虑如何将多分类问题转化为二分类问题。为此，我们先考察一个可以用 “Yes/No” 来回答的问题。比如，让神经网络来回答 “当上下文是 you 和 goodbye 时，目标词是 say 吗？” 这个问题，这时输出层只需要一个神经元即可。可以认为输出层的神经元输出的是 say 的得分。

那么，使用 CBOW 模型来处理如下图4-7所示。

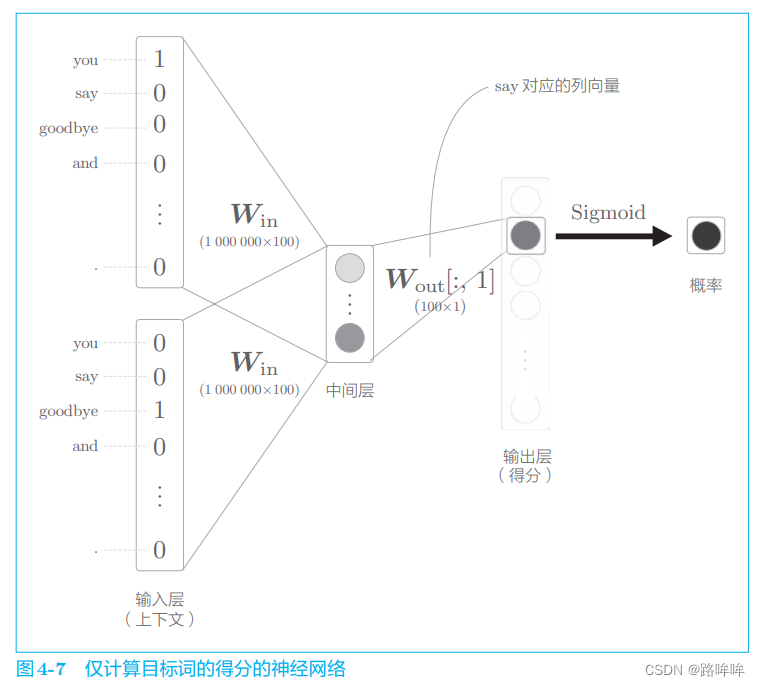
如图 4-7 所示，输出层的神经元仅有一个。因此，要计算中间层和输出侧的权重矩阵的乘积，只需要提取 say 对应的列（单词向量），并用它与中间层的神经元计算内积即可。这个计算的详细过程如图 4-8 所示。

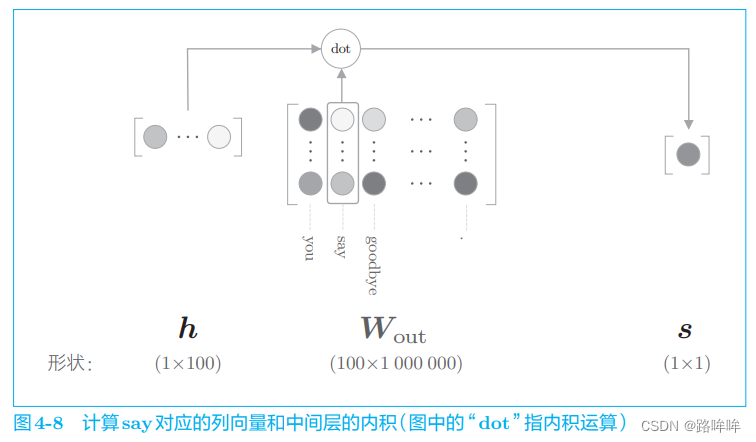
如图 4-8 所示，输出侧的权重 $W_{out}$ 中保存了各个单词 ID 对应的单词向量。此处，我们提取 say 这个单词向量，再求这个向量和中间层神经元的内积，这就是最终的得分。

到目前为止，输出层是以全部单词为对象进行计算的。这里，我们仅关注单词 say，计算它的得分。然后，使用 sigmoid 函数将其转化为概率。

4.2.3 sigmoid 函数和交叉熵误差

要使用神经网络解决二分类问题，需要使用 sigmoid 函数将得分转化为概率。为了求损失，我们使用交叉熵误差作为损失函数。

sigmoid 函数公式：
$$y=\frac{1}{1+exp(-x)}$$
上式 的图像如图 4-9 中的右图所示。从图中可以看出，sigmoid 函数呈 S 形，输入值 x 被转化为 0 到 1 之间的实数。这里的要点是，sigmoid 函数的输出 y 可以解释为概率。 另外，与 sigmoid 函数相关的 Sigmoid 层已经实现好了，如图 4-9 中的 左图所示。

通过 sigmoid 函数得到概率 y 后，可以由概率 y 计算损失。与多分类一 样，用于 sigmoid 函数的损失函数也是交叉熵误差，其数学式如下所示：
$$L=-(tlogy+(1-t)log(1-y))$$
其中，y 是 sigmoid 函数的输出，t 是正确解标签，取值为 0 或 1：

• t 取值为 1 时表示正确解是 “Yes”，输出 $-logy$；
• t 取值为 0 时表示正确解是 “No”，输出 $-log(1-y)$。

下面，我们用图来表示 Sigmoid 层和 Cross Entropy Error 层，如图 4-10 所示。

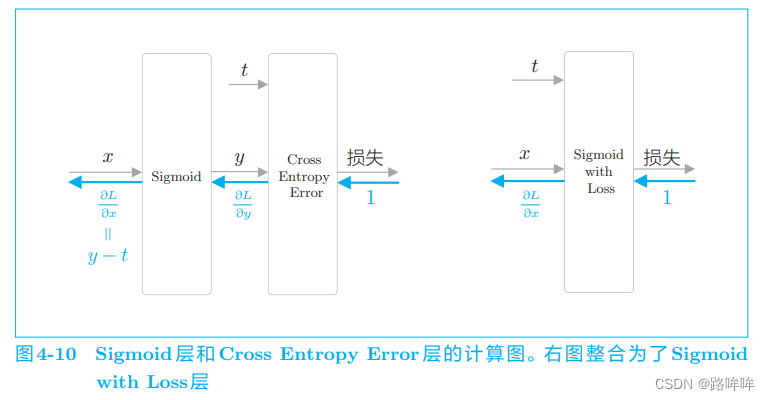
图 4-10 中值得注意的是反向传播的 $y-t$ 这个值。y 是神经网络输出的概率，t 是正确解标签，$y-t$ 正好是这两个值的差。这意味着，当正确解标签是 1 时，如果 y 尽可能地接近 1（100%），误差将很小。反过来，如果 y 远离 1，误差将增大。随后，这个误差向前面的层传播，当误差大时，模型学习得多；当误差小时，模型学习得少 。

4.2.4 多分类到二分类的实现

前面我们处理了多分类问题，在输出层使用了与词汇量同等数量的神经元，并将它们传给了 Softmax 层。如果把重点放在“层”和“计算”上，则此时的神经网络可以画成图 4-11。

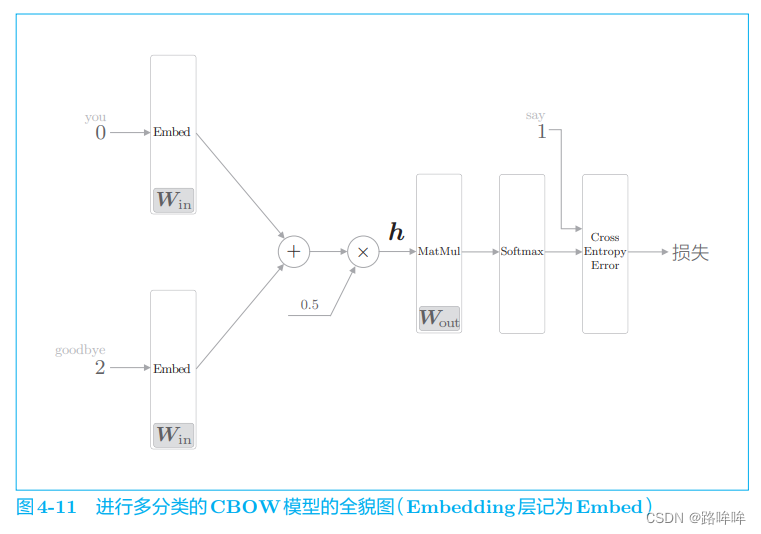
图 4-11 中展示了上下文是 you 和 goodbye 作为正确解的目标词是 say 的例子（假定 you 的单词 ID 是 0，say 的单词 ID 是 1，goodbye 的单 词 ID 是 2）。在输入层中，为了提取单词 ID 对应的分布式表示，使用了 Embedding 层。

现在，我们将图 4-11 中的神经网络转化成进行二分类的神经网络，网络结构如图 4-12 所示。

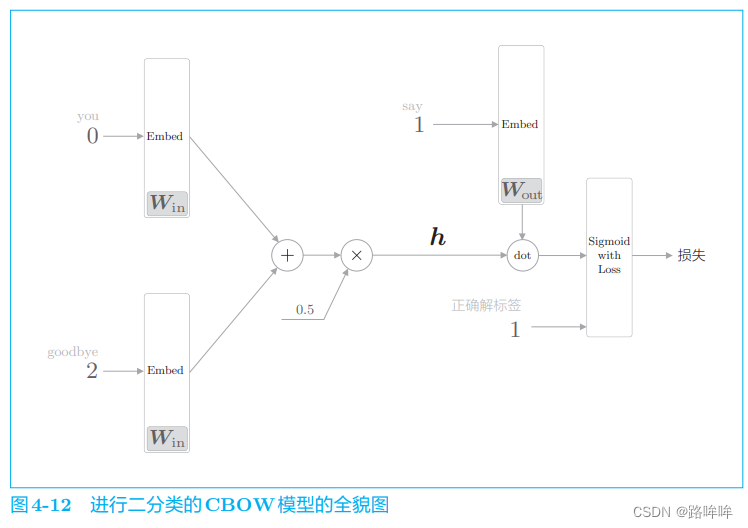
这里，将中间层的神经元记为 h，并计算它与输出侧权重 $W_{out}$ 中的单 词 say 对应的单词向量的内积。然后，将其输出输入 Sigmoid with Loss 层，得到最终的损失。

在图 4-12 中，向 Sigmoid with Loss 层输入正确解标签 1，这意味着现在正在处理的问题的答案是“Yes”。当答案是“No”时， 向 Sigmoid with Loss 层输入 0。

为了便于理解后面的内容，我们把图 4-12 的后半部分进一步简化。为 此，我们引入 Embedding Dot 层，该层将图 4-12 中的 Embedding 层和 dot 运算（内积）合并起来处理。使用这个层，图 4-12 的后半部分可以画成图 4-13。

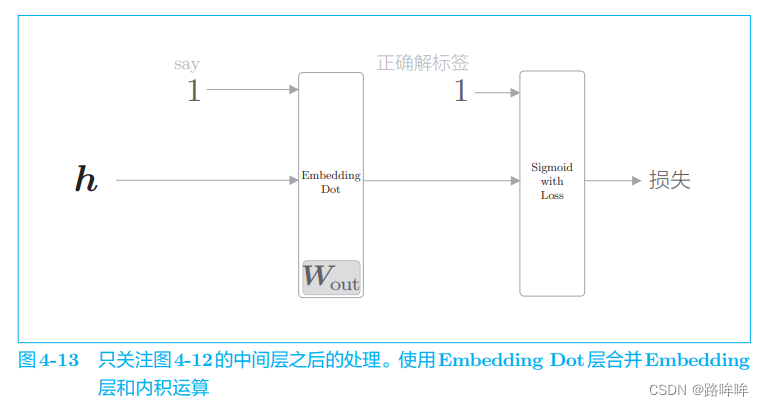
中间层的神经元 h 流经 Embedding Dot 层，传给 Sigmoid with Loss 层。从图中可以看出，使用 Embedding Dot 层之后，中间层之后的处理被简化了。

具体实现见书（后续再补充）

4.2.5 负采样

至此，我们成功地把要解决的问题从多分类问题转化成了二分类问题。但是，这样问题就被解决了吗？很遗憾，事实并非如此。因为我们目前仅学习了正例（正确答案），还不确定负例（错误答案）会有怎样的结果。

现在，我们再来思考一下之前的例子。在之前的例子中，上下文是 you 和 goodbye，目标词是 say。我们到目前为止只是对正例 say 进行了二分类， 如果此时模型有“好的权重”，则 Sigmoid 层的输出（概率）将接近 1。用计算图来表示此时的处理，如图 4-15 所示。

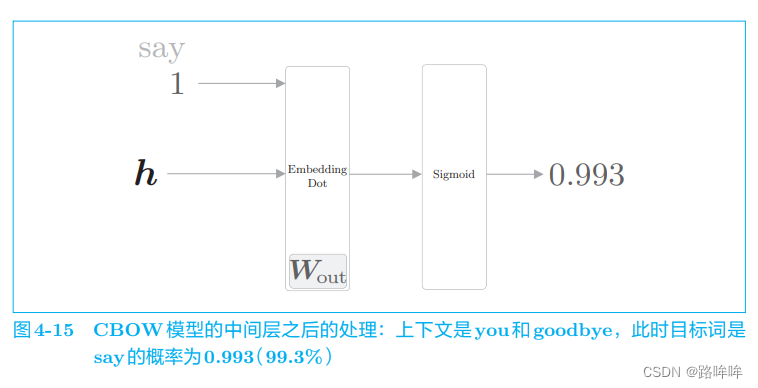
当前的神经网络只是学习了正例 say，但是对 say 之外的负例一无所知。 而我们真正要做的事情是，对于正例（say），使 Sigmoid 层的输出接近 1； 对于负例（say 以外的单词），使 Sigmoid 层的输出接近 0。用图来表示，如图 4-16 所示。

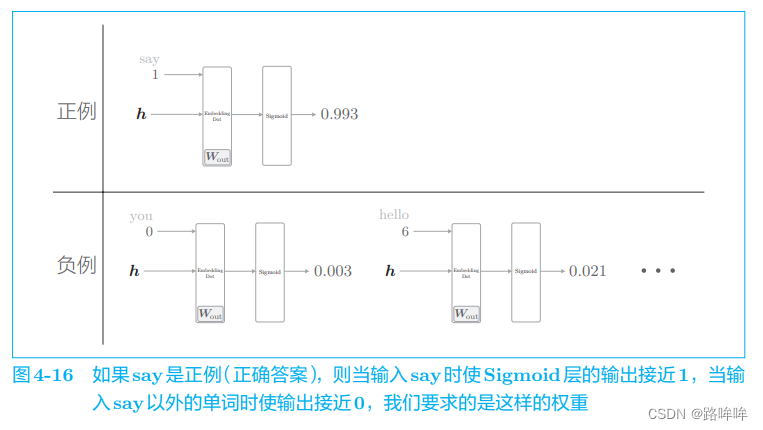
比如，当上下文是 you 和 goodbye 时，我们希望目标词是 hello（错误答案）的概率较低。在图 4-16 中，目标词是 hello 的概率为 0.021（2.1%），我们要求的就是这种能使输出接近 0 的权重。

为了把多分类问题处理为二分类问题，对于“正确答案”（正例）和“错误答案”（负例），都需要能够正确地进行分类（二分类）。因此，需要同时考虑正例和负例。

那么，我们需要以所有的负例为对象进行学习吗？答案显然是“No”。 如果以所有的负例为对象，词汇量将暴增至无法处理（更何况本章的目的本来就是解决词汇量增加的问题）。为此，作为一种近似方法，我们将选择若干个（5 个或者 10 个）负例（如何选择将在下文介绍）。也就是说，只使用少数负例。这就是负采样方法的含义。

总而言之，负采样方法既可以求将正例作为目标词时的损失，同时也可以采样（选出）若干个负例，对这些负例求损失。然后，将这些数据（正例 和采样出来的负例）的损失加起来，将其结果作为最终的损失。

下面，让我们结合具体的例子来说明。这里使用与之前相同的例子（正例目标词是 say）。假设选取 2 个负例目标词 hello 和 i，此时，如果我们只关注 CBOW 模型的中间层之后的部分，则负采样的计算图如图 4-17 所示。

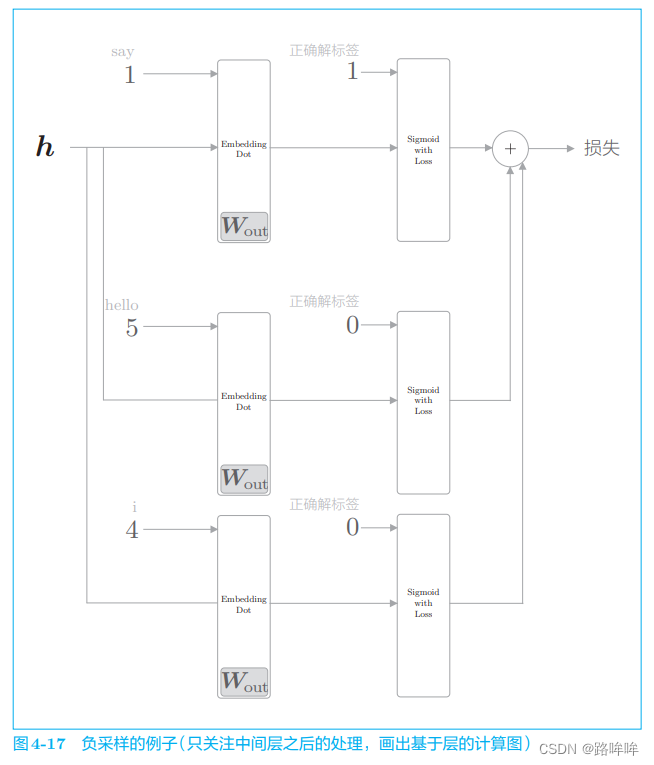
图 4-17 中需要注意的是对正例和负例的处理。正例（say）和之前一样， 向 Sigmoid with Loss 层输入正确解标签 1；而因为负例（hello 和 i）是错误答案，所以要向 Sigmoid with Loss 层输入正确解标签 0。此后，将各个数据的损失相加，作为最终损失输出。

4.2.6 负采样的采样方法

基于语料库的统计数据进行采样的方法比随机抽样要好。具体来说，就是让语料库中经常出现的单词容易被抽到，让语料库中不经常出现的单词难以被抽到。

基于语料库中单词使用频率的采样方法会先计算语料库中各个单词的出现次数，并将其表示为“概率分布”，然后使用这个概率分布对单词进行采样（图 4-18）

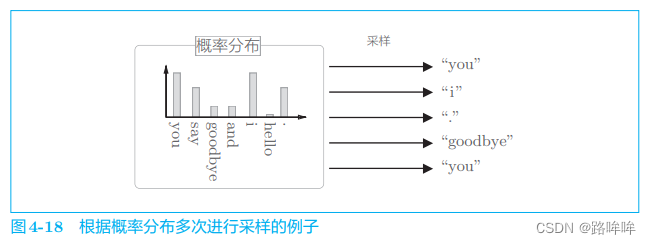
基于语料库中各个单词的出现次数求出概率分布后，只需根据这个概率分布进行采样就可以了。通过根据概率分布进行采样，语料库中经常出现的单词将容易被抽到，而“稀有单词”将难以被抽到。

负采样应当尽可能多地覆盖负例单词，但是考虑到计算的复杂度，有必要将负例限定在较小范围内（5 个或者 10 个）。这里，如果只选择稀有单词作为负例会怎样呢？结果会很糟糕。因为在现实问题中， 稀有单词基本上不会出现。也就是说，处理稀有单词的重要性较低。 相反，处理好高频单词才能获得更好的结果。

使用 Python 来说明基于概率分布的采样。为此，可以使用 NumPy 的 np.random.choice() 方法。

import numpy as np

# 从0到9的数字中随机选择一个数字
np.random.choice(10)  # 7
np.random.choice(10)  # 2

# 从words列表中随机选择一个元素
words = ['you', 'say', 'goodbye', 'I', 'hello', '.']
np.random.choice(words)  # 'goodbye'

# 有放回采样5次
np.random.choice(words, size=5)  # array(['goodbye', '.', 'hello', 'goodbye', 'say'], dtype='<U7')

# 无放回采样5次
np.random.choice(words, size=5, replace=False)  # array(['hello', '.', 'goodbye', 'I', 'you'], dtype='<U7')

# 基于概率分布进行采样
p = [0.5, 0.1, 0.05, 0.2, 0.05, 0.1]
np.random.choice(words, p=p)  # 'you'

如上所示，np.random.choice() 可以用于随机抽样。如果指定 size 参数，将执行多次采样。如果指定 replace=False，将进行无放回采样。通过给参数 p 指定表示概率分布的列表，将进行基于概率分布的采样。剩下的就是使用这个函数抽取负例。

word2vec 中提出的负采样对刚才的概率分布增加了一个步骤。如下式所示，对原来的概率分布取 0.75 次方。
$$P^{\prime }(w_i)=\frac{P(w_i{)}^{0.75}}{{\sum }_j^{n}P(w_j{)}^{0.75}}$$
这里，$P(w_i)$ 表示第 $i$ 个单词的概率。上式只是对原来的概率分布的各个元素取 $0.75$ 次方。不过，为了使变换后的概率总和仍为 1，分母需要变成 “变换后的概率分布的总和” 。

这样做的目的是为了防止低频单词被忽略。更准确地说，通过取 0.75 次方，低频单词的概率将稍微变高。

看一个具体例子，如下所示。

p = [0.7, 0.29, 0.01]
new_p = np.power(p, 0.75)
new_p /= np.sum(new_p)
print(new_p)
# [0.64196878 0.33150408 0.02652714]

根据这个例子，变换前概率为 0.01（1%）的元素，变换后为 0.026 … （2.6 …%）。通过这种方式，取 0.75 次方作为一种补救措施，使得低频单词稍微更容易被抽到。此外，0.75 这个值并没有什么理论依据，也可以设置成 0.75 以外的值。

4.2.7 负采样的实现

见书

4.3 改进版 word2vec 的学习

见书

4.4 wor2vec 相关的其他话题

4.4.1 word2vec 的应用例

使用 word2vec 获得的单词的分布式表示可以用来查找近似单词，但是单词的分布式表示的好处不仅仅在于此。

在自然语言处理领域，单词的分布式表示之所以重要，原因就在于迁移学习（transfer learning）。迁移学习是指在某个领域学到的知识可以被应用于其他领域。

4.4.2 单词向量的评价方法

我们最终想要的是一个高精度的系统。这里我们必须考虑到的是，这个系统（比如情感分析系统）是由多个子系统组成的。所谓多个子系统，拿刚才的例子来说，包括生成单词的分布式表示的系统（word2vec）、对特定问题进行分类的系统（比如进行情感分类的 SVM 等）。

单词的分布式表示的学习和分类系统的学习有时可能会分开进行。在这种情况下，如果要调查单词的分布式表示的维数如何影响最终的精度，首先需要进行单词的分布式表示的学习，然后再利用这个分布式表示进行另一个机器学习系统的学习。换句话说，在进行两个阶段的学习之后，才能进行评价。在这种情况下，由于需要调试出对两个系统都最优的超参数，所以非常费时。

因此，单词的分布式表示的评价往往与实际应用分开进行。此时，经常使用的评价指标有“相似度”和“类推问题”

单词相似度的评价通常使用人工创建的单词相似度评价集来评估。比如，cat 和 animal 的相似度是 8，cat 和 car 的相似度是 2……类似这样， 用 0 ～ 10 的分数人工地对单词之间的相似度打分。然后，比较人给出的分数和 word2vec 给出的余弦相似度，考察它们之间的相关性。

类推问题的评价是指，基于诸如 “king : queen = man : ?” 这样的类推问题，根据正确率测量单词的分布式表示的优劣。比如，论文 [27] 中给出 了一个类推问题的评价结果，其部分内容如图 4-23 所示。

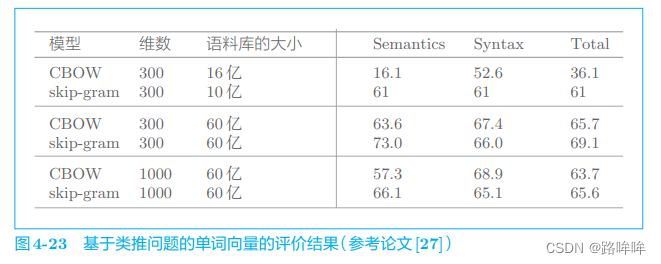
在图 4-23 中，以 word2vec 的模型、单词的分布式表示的维数和语料库的大小为参数进行了比较实验，结果在右侧的 3 列中。图 4-23 的 Semantics 列显示的是推断单词含义的类推问题（像“king : queen = actor : actress” 这样询问单词含义的问题）的正确率，Syntax 列是询问单词形态信息的问题，比如“bad : worst = good : best”。

基于类推问题可以在一定程度上衡量“是否正确理解了单词含义或语法问题”。因此，在自然语言处理的应用中，能够高精度地解决类推问题的单词的分布式表示应该可以获得好的结果。但是，单词的分布式表示的优劣对目标应用贡献多少（或者有无贡献），取决于待处理问题的具体情况，比如应用的类型或语料库的内容等。也就是说，不能保证类推问题的评价高，目标应用的结果就一定好。这一点请一定注意。