Mean Value Coordinates for Closed Triangular Meshes 发表于ACM SIGGRAPH 2003, 是图形学领域的经典论文，作者是之前组里毕业的居涛，论文只有6页，这在SIGGRAPH会议中并不多见，目前引用超过700次，在插值，参数化，变形等领域被广泛应用。

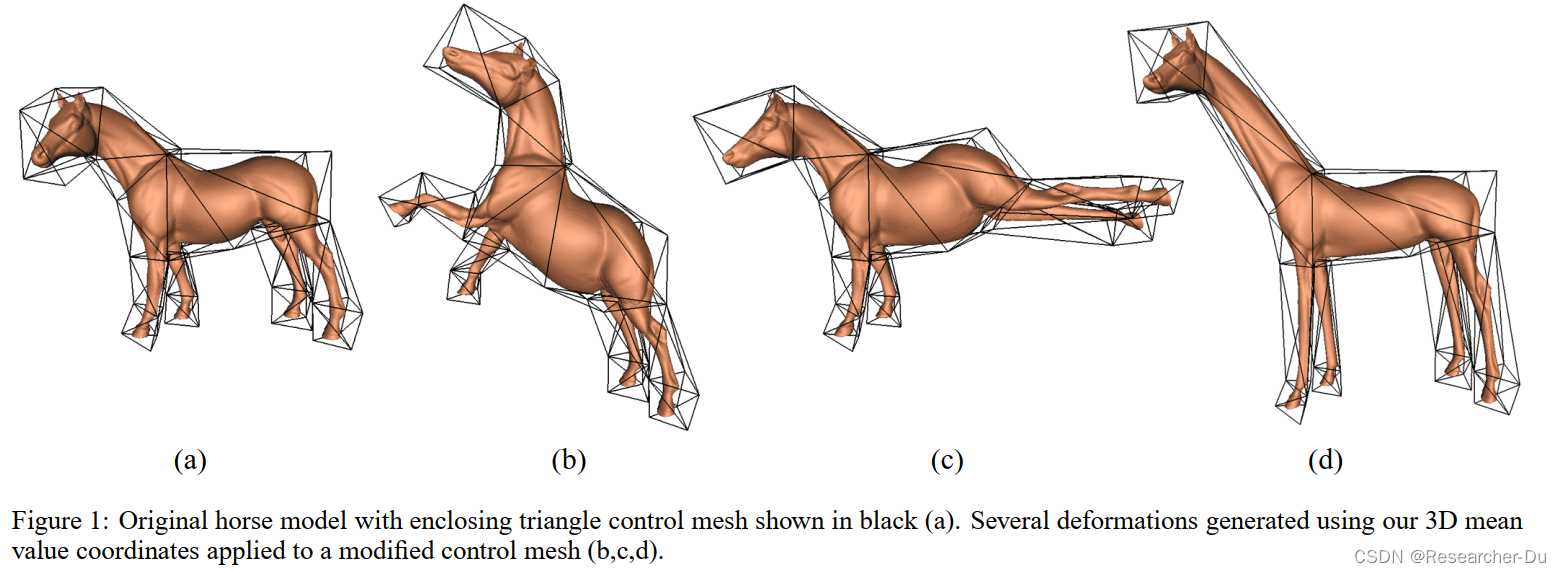
先看一下论文给的Teaser，这里主要是变形的一个应用。输入包括：待变形网格模型 + 控制网格（跟模型形状相似的稀疏网格），通过移动控制网格的顶点驱动模型形状发生改变，其实主要就是插值问题，将模型顶点表示为控制网格点的线性组合。

一、插值问题描述

本文所涉及的插值要做的事就是将2D多边形(3D多面体) $P$ 内部的任意点 $v$ 表示为$P$ 的线性组合：
$$v=\sum _{i=1}^n{w}_i{p}_i\text{\hspace{1em}(1)}$$
这里的 $w_i$ 称为插值权重，满足 ${\sum }_{i=1}^n{w}_i=1$，插值问题的重点就是求解该权重。对于上图所示的变形问题，其实就是求出该权重并保持不变，然后修改控制网格: $P\to P^{\prime }$, 最后，变形后的模型表示为：$v^{\prime }={\sum }_{i=1}^n{w}_i{p}_i^{\prime }$ 。

二、2D多边形插值

这一部分主要探讨2D多边形内部插值，输入多边形 $P$, 内部一点 $v$, 输出对应的插值权重 W = { w i } W=\{w_i\} W={wi​}。

如上图左所示，我们首先画一个以 $v$为圆心的单位圆，将 $v$ 与各个多边形顶点连接的话，多边形每条边会对应到一段圆弧。

不失一般性，以 第一条边 $p_1{p}_2$ 对应的圆弧为例，我们将$v$ 指向这段圆弧上所有点的单位向量求和(积分)得到的向量 $m_1$ 称为均值向量（mean vector）。 $m_1$ 可以通过一组基 $v{p}_1=p_1-v,v{p}_2=p_2-v$ 进一步表示为:

$${\lambda }_1^1(p_1-v)+{\lambda }_1^2(p_2-v)=m_1\text{\hspace{1em}(2)}$$
其中，${\lambda }_1^1$ 和 ${\lambda }_1^2$ 分别表示 $m_1$ 在这组基上的坐标值。另外，Floater曾在他的论文中给出了均值向量的表示形式：
Floater M S. Mean value coordinates[J]. Computer aided geometric design, 2003, 20(1): 19-27.

$$m_1=\tan [\alpha /2]\left(\frac{\left(p_1-v\right)}{\left|p_1-v\right|}+\frac{\left(p_2-v\right)}{\left|p_2-v\right|}\right)\text{\hspace{1em}(3)}$$

其中，$\alpha$ 是向量 $v{p}_1,v{p}_2$ 之间的夹角。根据(2)(3)，我们就可以直接得出：
$${\lambda }_1^1=\frac{tan[\alpha /2]}{|p_1-v|},{\lambda }_1^2=\frac{tan[\alpha /2]}{|p_2-v|}\text{\hspace{1em}(4)}$$

那么，我们怎么根据上式导出插值权重呢？继续往下看。

注意（2）式只是针对第一条线段 $p_1{p}_2$ 计算了均值向量 $m_1$，如果计算所有线段对应的均值向量，并对其求和，那么这些均值像之和为0向量。 相当于，圆心指向圆弧所有点构成的单位向量之和，必然为0，因为任意一个单位向量都存在一个方向相反的向量。也就是说：
$$\{\begin{array}{r}{\lambda }_1^1(p_1-v)+{\lambda }_1^2(p_2-v)=m_1\\ {\lambda }_2^1(p_2-v)+{\lambda }_2^2(p_3-v)=m_2\\ ...\\ {\lambda }_n^1(p_n-v)+{\lambda }_n^2(p_1-v)=m_n\end{array}$$

$$m_1+m_2+...+m_n=0$$

上述任意一组${\lambda }_i^1$,${\lambda }_i^2$均可通过（4）求解得到。因为任意 $p_i-v$ 均出现两次（一个端点被两条边共享），因此重新整理上式为：
$$({\lambda }_1^1+{\lambda }_n^2)(p_1-v)+({\lambda }_1^2+{\lambda }_2^1)(p_2-v)+...+({\lambda }_{n-1}^2+{\lambda }_n^1)(p_n-v)=0\text{\hspace{1em}(5)}$$

我们令 $k_1=({\lambda }_1^1+{\lambda }_n^2)$, $k_2=({\lambda }_1^2+{\lambda }_2^1)$,…,$k_n=({\lambda }_{n-1}^2+{\lambda }_n^1)$, 上次可以进一步写为：
$$k_1(p_1-v)+k_2(p_2-v)+...+k_n(p_n-v)=0\text{\hspace{1em}(6)}$$

接下来，令 $K=k_1+k_2+...+k_n$, $w_1=k_1/K,w_2=k_2/K,...w_n=k_n/K$， 上式可以进一步改写为：
$$w_1(p_1-v)+w_2(p_2-v)+...+w_n(p_n-v)=\sum _{i=1}^n{w}_i(p_i-v)=0\text{\hspace{1em}(7)}$$

我们发现 （7）跟（1）完全等价，因为 ${\sum }_{i=1}^n{w}_i=1$, $v={\sum }_{i=1}^n{w}_{i}v$。到此为止，我们得到了满足（1）式的插值权重也就是均值坐标。

三、3D多面体插值

在2D多边形中，我们通过将多边形投影到单位圆上求解均值坐标。容易想到，在3D多面体内部，我们可以将多面体投影到单位球来计算给定点的均值坐标。

如上图所示，我们将多面体投影到单位球面。如上图(3)所示，多面体上的任意三角面片对应单位球上的一个球面三角形，那么从$v$ 指向该球面三角形上所有点的单位向量的积分称为该球面三角形的均值向量 $m$。文中给出了这一向量的计算方式（证明明详见论文）：
$$m=\sum _{i=1}^3\frac{1}{2}{\theta }_i{n}_i\text{\hspace{1em}(8)}$$
接下来，通过上图(5)所示的示例进行讲解，其均值向量可以表示为：
$$m=\frac{1}{2}({\theta }_1{n}_1+{\theta }_2{n}_2+{\theta }_3{n}_3)\text{\hspace{1em}(9)}$$
其中，${\theta }_1,{\theta }_2,{\theta }_3$ 分别是 $(v{p}_2,v{p}_3),(v{p}_1,v{p}_3),(v{p}_1,v{p}_2)$ 的夹角，$n_1,n_2,n_3$ 分别是 $(v{p}_2{p}_3),(v{p}_1{p}_3),(v{p}_1{p}_2)$ 平面的法向。另一方面，球面三角形上的均值向量 $m$, 仍然可以通过一组基 $(v{p}_1,v{p}_2,v{p}_3)$ 表示出来：
$$m={\lambda }_1(p_1-v)+{\lambda }_2(p_2-v)+{\lambda }_3(p_3-v)\text{\hspace{1em}(10)}$$

如何求解上述 $\lambda$呢？因为$n_1$是平面 $(v{p}_2{p}_3)$ 的法向量，所以 $n_1\cdot (p_2-v)=0$, $n_1\cdot (p_3-v)=0$，其它类似，那么有：
$$\{\begin{array}{r}{n}_{1}m=n_1{\lambda }_1(p_1-v)+0+0\\ n_{2}m=0+n_2{\lambda }_2(p_2-v)+0\\ n_{3}m=0+0+n_3{\lambda }_3(p_3-v)\end{array}$$
所以：
$$\{\begin{array}{r}{\lambda }_1=\frac{n_{1}m}{n_1(p_1-v)}\\ \\ {\lambda }_2=\frac{n_{2}m}{n_2(p_2-v)}\\ \\ {\lambda }_3=\frac{n_{3}m}{n_3(p_3-v)}\end{array}\text{\hspace{1em}(11)}$$

类似的，上式只是计算了多面体上一个三角面片对应的球面三角形的均值向量，以及对应的三个点的贡献。如果将所有三角面片投影到球面上，那么所有球面三角形的均值向量之和为0. 也就是：
$$\sum _{T=1}^n{\lambda }_T^1(p_T^1-v)+{\lambda }_T^2(p_T^2-v)+{\lambda }_T^3(p_T^3-v)=0\text{\hspace{1em}(12)}$$
其中，$T$表示遍历多面体 $P$ 的所有三角形，$p_T^1,p_T^2,p_T^3$ 表示某个三角形 $T$ 的3个顶点。上式 ${\lambda }_T^1,{\lambda }_T^2,{\lambda }_T^3$ 通过（11）式子计算。最后的最后，上式等价于：
$$\sum _{i=1}^n{w}_i(p_i-v)=0$$
这个过程跟2D的推导类似，最终归一化的权重 $w_i$ 可以表示为：
$$w_i=\frac{{\sum }_{T\in N(i)}{\sum }_{j=1}^3{\lambda }_T^j\cdot (p_T^i==p_i)}{{\sum }_{T=1}^n({\lambda }_T^1+{\lambda }_T^2+{\lambda }_T^3)}\text{\hspace{1em}(13)}$$

也就是说，每个点的权重，跟所关联的所有三角形相关。 文中还有一些数值稳定性的优化方案，就不再描述。可以参看原文伪代码。

参考资料

[1] Floater M S. Mean value coordinates[J]. Computer aided geometric design, 2003, 20(1): 19-27.
[2] Tao Ju et al. Mean Value Coordinates for Closed Triangular Meshes
[3] 以及对应的slides： https://people.engr.tamu.edu/schaefer/teaching/689_Fall2006/talks/meanvalue.pdf