第2章 数据的类型

本章我们介绍数据的类型，主要包含以下主题：

• 结构化数据(structured data)和非结构化数据(unstructured data)
• 定量数据(quantitative data)和定性数据(qualitative data)
• 数据的4个尺度

2.2 为什么要进行区分

2.3 结构化数据和非结构化数据

我们拿到数据集后，想知道的第一件事情就是数据集是结构化还是非结构化。

• 结构化数据(structured data)：指特征和观察值以表格形式存储（行列结构）
• 非结构化数据(unstructured data)：指数据以自由实体形式存在，不符合任何标准的组织层次结构，比如行列结构

以下几个例子可以帮助我们更好地理解两者的区别。

• 大部分文本格式数据都是非结构化数据，比如服务器日志、Facebook帖子等。
• 科学家严格记录的科学实验观察值，以极其有序和结构化的格式存储，属于结构化数据。
• 化学核苷酸的基因序列（比如ACGTATTGGCA）是非结构化数据。虽然核苷酸有其独特的顺序，但我们暂时还不能以行列结构表示整体的顺序。

通常情况下，结构化数据最容易处理和分析。事实上，大部分统计学模型和机器学习模型都只适用于结构化数据，而不能很好地应用在非结构化数据中。

既然行列结构数据最适合人和机器的分析，为什么我们还要研究非结构化数据呢？因为它太常见了！根据预测，世界上 80%~90%的数据是非结构化数据，它们以各种形式存储在全球各地，是一个尚未被人类察觉的巨大数据源。

虽然数据科学家喜欢结构化数据，但也必须有能力处理日益庞大的非结构化数据。因为如果这个世界上 90%的数据都是非结构化数据，这意味着世界上 90%的信息都被揉捏在一个更难处理的格式中一一推文、邮件、文献和服务器日志等。

既然大部分数据都是自由格式的非结构化数据，我们就需要使用一种叫“预处理(preprocessing)”的技术将其转化为结构化数据，以便做进一步的分析。下面我们将介绍把非结构化数据转换为结构化数据的常用方法。在下一章，我们将介绍数据预处理的更多细节。

将非结构化数据处理(组织)成结构化数据，由无序到有序

案例：数据预处理

当我们处理文本数据（通常被认为是非结构化）时，有很多方法可以将其转化为结构化格式。比如，使用以下描述文本特征的数据：

• 字数/短语数
• 特殊符号
• 文本相对长度
• 文本主题

我们用以下推文作为案例。

This Wednesday morn, are you early to rise? Then look East. The Crescent Moon joins Venus & Saturn. Afloat in the dawn skies.

除此之外，通过数据预处理，我们还可以利用数据现有的特征生成新特征。比如，通过统计以上推文的字数或特殊符号生成的新特征。

字数/短语数

我们可以通过字数或短语数对推文进行拆分。比如单词“this”在推文中出现了 1次，以此类推。我们用结构化的格式表示这条推文，这样就把非结构化文本转换成行列格式。

	this	Wednesday	morn	are	this Wednesday
文本计数	1	1	1	1	1

为了进行以上转换，我们使用了上一章介绍的 scikit-learn模块中的 CountVectorizer方法。

特殊符号

我们还可以统计是否含有特殊符号，比如问号和感叹号。这些符号通常隐含着某种看法，但很难被发现。事实上，问号在以上推文中出现了 1 次，这意味着该推文给读者提出了一个问题。我们可以在刚才的表格中添加一列。

	this	Wednesday	morn	are	this Wednesday	?
文本计数	1	1	1	1	1	1

文本相对长度

这条推文有121个字符。

len("This Wednesday morn,are you early to rise?Then look East.The Crescent Moon joins Venus & Saturn.Afloat in the dawn skies.")
#121

分析师发现推文的平均长度是 30 个字符。所以，我们可以增加一个叫“相对长度”的新特征，用来表示这条推文的长度相对平均推文长度的倍数。简单计算可知，这条推文是平均推文长度的 4.03 倍。

我们可以在刚才的表格中再新增一列。

	this	Wednesday	morn	are	this Wednesday	?	相对长度
文本计数	1	1	1	1	1	1	4.03

文本主题

我们可以为推文添加相应主题，比如这条推文属于天文学，所以我们可以在刚才的表格中继续增加一列。

	this	Wednesday	morn	are	this Wednesday	?	相对长度	主题
文本计数	1	1	1	1	1	1	4.03	天文学

以上我们展示了如何将一段文本转换为结构化、有组织的数据格式，以便进行数据探索和使用模型。

在 Python 中，计算推文长度和统计字数都非常简单，为文本分配主题则是唯一一个无法从原始文本中自动提取的新特征。幸运的是借助更先进的主题模型(topic models),我们能够从自然语言中提取和预测相关主题。

Maybe we can use ChatGpt API

未来，快速识别数据集是结构化还是非结构化，将为你节省数小时甚至几天的工作时间。一旦你能够识别以上特征，下一步将是识别数据集中的每个独立特征。

2.4 定量数据和定性数据

定量数据还是定性数据是描述数据集特征最常用的一种方式。

大多数时候，定量数据通常指（并不总是）以行列结构存储的结构化数据集。

定量数据和定性数据的定义如下。

• 定量(quantitative)数据:通常用数字表示，并支持包括加法在内的数学运算。
• 定性(qualitative)数据:通常用自然类别和文字表示，不支持数学格式和数学运算。

2.4.1 案例：咖啡店数据

假设我们在分析一家坐落于某大城市的咖啡店数据，数据集有以下5个字段（特征）。

数据：咖啡店

• 咖啡店名称
• 营业额（单位：千元）
• 邮政编码
• 平均每月客户数
• 咖啡产地

以上特征都可以被归类为定量数据或定性数据，这一简单的区分意义非常重大。下面我们逐个进行分析。

• 咖啡店名称：定性数据

咖啡店名称无法用数字表示，并且咖啡店名称不能进行数字运算。

• 营业额：定量数据

咖啡店的营业额可以用数字表示，并且营业额支持简单的数学运算。比如将12个月的营业额相加可得到1年的营业额。

• 邮政编码：定性数据

邮政编码有点复杂。虽然邮政编码通常用数字表示，但它是定性数据，因为邮政编码不符合定量数据的第二个要求——支持数学运算。两个邮政编码相加得到的是一个没有意义的数字，而不是一个新的邮政编码。

• 平均每月客户数：定量数据

该指标可以用数字表示，且支持简单的数学运算——将每个月的平均客户数相加可以得到全年的客户数。

• 咖啡产地：定性数据

我们假设这是一家只使用单一咖啡产地的小型咖啡馆，咖啡产地用国家名字（比如埃塞俄比亚、哥伦比亚）而非数字表示。

两个重要提醒：

• 虽然邮政编码通常用数字表示，但它并不是定量数据，因为对邮政编码求和或者求平均值，得到的结果没有任何意义。
• 大部分情况下，当字段值为文本时，该字段都是定性数据。

如果你在区分数据类型时遇到困难，那么下决定之前，可以先问自己几个简单的问题。

• 该字段可以用数字表示吗？

  如果不可以，该字段是定性数据。

  如果可以，进入下一个问题。

• 将该字段的多个值相加，得到的新数字有意义吗？

  如果没有意义，该字段是定性数据。

  如果有意义，该字段是定量数据。

这个方法可以帮助你区分大部分数据的定量/定性属性。

2.4.2 案例：世界酒精消费量

世界卫生组织发布了一个世界各国饮酒习惯的数据集。我们将使用Python和数据探索工具Pandas对该数据集进行分析。

import pandas as pd

#read in the CSV file
drinks=pd.read_csv('data/drinks.csv')
#examine the data's first five rows
drinks.head()

以上3行代码的作用是：

• 导入Pandas包，并缩写为pd
• 读取CSV文件，并命名为drinks
• 调用head方法，返回数据集的前5行

CSV文件传入的是整齐的行列结构数据，如图2.1所示

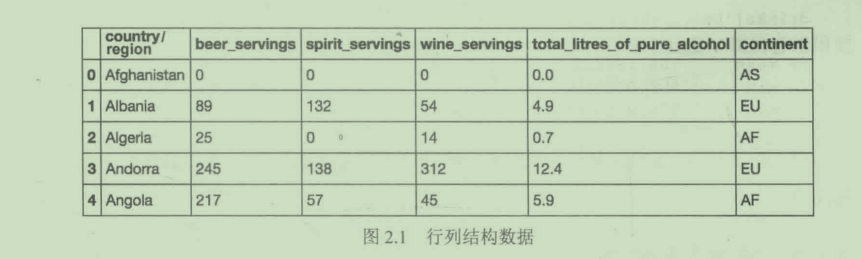
在本例中，我们有6列不同的数据。

• country/region: 定性数据
• beer_servings: 定量数据
• spirit_servings: 定量数据
• wine_servings: 定量数据
• total_litres_of_pure_alcohol: 定量数据
• continent: 定性数据

我们首先来看定性数据continent列。我们可以使用Pandas计算该定性特征列的基本汇总统计指标。此处使用describe()方法，该方法首先判断字段的定性/定量属性，然后给出基本统计信息。所示如下：

drinks['continent'].describe()

>>count    193
>>unique     5
>>top       AF
>>freq      53

以上结果显示世界卫生组织收集的数据来自5个不同的洲，在193个观测值中，AF（非洲）最高频出现了53次。

如果我们在定量数据中使用同样的方法，将得到不同的结果：

drinks['beer_servings'].describe()

>>mean    106.160622
>>min       0.000000
>>max     376.000000 

以上结果显示，这些国家和地区的人均啤酒消费量是106.2升，其中消费量最少的是0，最高的是376升。

2.4.3 更深入的研究

定量数据还可以继续细分为离散型 (discrete)数据和连续型 (continuous)数据。它们的定义如下。

• 离散型数据：通常指计数类数据，取值只能是自然数或整数。

比如，掷骰子的点数属于离散型，因为骰子的点数只有 6 个值。咖啡馆的人数属于离散型，因为人数不能用无理数和负数表示。

• 连续型数据： 通常指测量类数据，取值为无限范围区间。

比如，体重可以是68千克，也可以是89.66千克，注意小数点，所以体重是连续型数据。人或建筑物的高度也属于连续型，因为取值可以是任意大小的小数。温度和时间同样属于连续型。

2.6 数据的4个尺度

通常情况下，结构化数据的每一列都可以被归为以下4个尺度中的一个。这4个尺度分别是：

1. 定类尺度(nominal level)
2. 定序尺度(ordinal level)
3. 定距尺度(interval level)
4. 定比尺度(ratio level)

随着尺度的深入，数据的结构化特征也将越来越多，也更有利于分析。每个尺度都有适用于自身的测量数据中心（the center of the data）的方法。比如，我们平时用来做数据中心的平均值，其实仅适用于特定尺度的数据。

2.6.1 定类尺度

第一个尺度是定类尺度，主要指名称或类别数据，如性别、国籍、种类和啤酒的酵母菌种类等。它们无法用数字表示，因此属于定性数据。以下是一些例子。

• 动物种类属于定类尺度，如大猩猩属于哺乳类动物。
• 演讲稿中的部分单词也属于定类尺度，如单词"she"既是代词，也是名词。

作为定性数据，定类尺度数据不能进行数学运算，如加法或除法，因为得到的结果是无意义的。

适用的数学运算

虽然定类尺度数据不支持基本的数学运算，但等式和集合隶属关系除外。

• ”成为科技创业者“等价于”从事科技行业“，反之则不成立；
• ”正方形“等价于”长方形“，反之则不成立。

测度中心

测度中心（measure of center）是一个描述数据趋势的数值，有时也被称为数据平衡点（balance point）。常见的测度中心有平均值、中位数和模。

定类尺度数据通常用**模（mode）**作为测度中心。比如，对于世界卫生组织的酒精消费量数据，出现次数最多的洲是Africa，因此Africa可以作为continent列的测度中心。

由于定类尺度数据既不能排序，也无法相加，因此中位数和平均值不能作为它的测度中心。

2.6.2 定序尺度

定类尺度数据无法按任何自然属性进行排序，这极大限制了定类尺度数据可使用的数学运算符。定序尺度数据则为我们提供了一个等级次序，换言之，提供了一个可以对观测值进行排序的方法。然而，它仍不支持计算两个观测值间的相对差异。也就是说，虽然我们能够对观测值进行排序，但观测值间相加或相减得到的结果仍然没有意义。

案例

李克特量表（Likert）是最常见的定序尺度数据。当我们用1~10填写满意度调查问卷时，生成的结果正是定序尺度数据。调查问卷答案必须介于1~10，并可以被排序，比如8分比7分好，9分比3分好。

然而，各个数字之间的差异并没有实际意义。比如7分和6分的差异是1分，2分和1分的差异也是1分，但两个1分的含义却可能完全不同。

适用的数学运算

“排序”指数据本身具有的自然顺序，然而有些时候还需要一些技巧。比如对于可见光谱——红、橙、黄、绿、蓝、靛蓝、紫，自然排序规则是随着光的能量和其他属性的增加，从左至右排序。

然而，艺术家如果有特殊需求，还可以用另一种排序规则，比如基于颜料用量对上述颜色进行排序。虽然新的排序规则会改变颜色顺序，但比排序规则本身更重要的是保持排序规则的一致性。

“比较”是定序尺度数据支持的另一个新运算符。对于定类尺度数据，度量值间的比较没有意义，比如一个国家“天然”比另一个国家好，演讲中某一段“天然”比另一段糟糕。但是对于定序数据，我们则可以对度量值进行比较，比如调查问卷中的7分比1分好。

测度中心

定序尺度通常用中位数(median)，而不是**平均值(mean/average)**表示测度中心，因为定序尺度数据不支持除法。当然，我们也可以使用定类尺度中介绍的模作为测度中心。

下面我们通过一个例子介绍中位数的用法。

假设你刚刚完成一份关于员工满意度的调查问卷，问题是“用1~5分为你当前的工作幸福程度打分”，以下是调研结果：

5,4,3,4,5,3,2,5,3,2,1,4,5,3,4,4,5,4,2,1,4,5,4,3,2,4,4,5,4,3,2,1

下面使用Python计算以上数据的中位数。很多人认为平均值也可以作为测度中心，这是不正确的，因为两个变量相减或相加得到的值无任何意义，比如4分减去2分，差异的2分没有任何意义，所以数学运算得出的平均值也没有任何意义。

import numpy
results=[5,4,3,4,5,3,2,5,3,2,1,4,5,3,4,4,5,4,2,1,4,5,4,3,2,4,4,5,4,3,2,1]
sorted_results=sorted(results)
print(sorted_results)
'''
[1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 5]
'''
print(numpy.mean(results))    #==3.4375
print(numpy.median(results))  #==4.0

不难发现，中位数4.0作为测度中心不仅是合理的，也让调查问卷结果变得更加直观。

简单回顾

2.6.3 定距尺度

对于定距尺度数据，我们可以用均值和其他更复杂的数学公式描述数据。这是定类尺度和定距尺度最大的差异，也是唯一的差异。

定距尺度数据可以进行有意义的减法运算。

案例

温度是最常见的定距尺度数据。假设得克萨斯的温度是 37.78℃，土耳其伊斯坦布尔的温度是 26.67℃，那么得克萨斯比伊斯坦布尔高 11.11℃。相对于调查问卷案例，这个例子允许的数学运算显然更多。

另外，虽然调查问卷数据看起来好像也属于定距尺度数据(因为使用 1~5 表示满意度)，但是请牢记，两个分数的差没有任何意义！正因为如此，调查问卷数据才不属于定距尺度。

适用的数学运算

我们可以使用低一级尺度的所有运算符（排序、比较等），以及下面两个新运算符：

• 加法
• 减法

通过以上两个新运算符，我们可以用全新的视角观察数据。

测度中心

对于定距尺度数据，我们依然可以用中位数和模来表示数据的测度中心，但更加准确的方法是用算术平均值(arithmetic mean)，通常简称为“均值(mean)”。回想一下均值的定义，均值要求我们对所有的观测值求和。由于定类和定序尺度数据不支持加法运算，因此均值对这两个尺度没有意义。只有定距尺度及以上尺度的数据，均值才有意义。

下面我们通过一个例子介绍均值的用法。

假设某冰箱保存着制药公司的疫苗，以下是该冰箱每小时的温度值（华氏度）：

31,32,32,31,28,29,31,38,32,31,30,29,30,31,26

继续用Python计算以上数据的均值和中位数。

import numpy
temps=[31,32,32,31,28,29,31,38,32,31,30,29,30,31,26]
print(numpy.mean(temps))     #==30.73
print(numpy.median(temps))   #==31.0

中位数和平均值非常接近，都在31℉（-0.56℃）左右。然而疫苗的存放标准要求是：

请勿将疫苗置于29℉（-1.67℃）之下！

我们注意到冰箱温度有两次低于29℉，但你认为这不足以对疫苗产生不利影响。下面我们用**变差测度(measure of variation)**判断冰箱状态是否正常。

变差测度

变差测度是之前没有出现过的内容。我们知道测度中心的重要性，但在数据科学中，了解数据分布的广度也同样重要，描述这一现象的度量叫作变差测度。你可能听说过标准差 (standard deviation)，并且直到现在还处于统计学课程给你造成的轻微创伤后精神压力症(PTSD)。但由于变差测度的概念太重要了，所以有必要对它进行简单说明。

变差测度(比如标准差) 是一个描述数据分散程度的数字。变差测度和测度中心是描述数据集最重要的两个数字。

标准差

标准差是定距尺度和更高尺度数据中应用最为广泛的变差测度。标准差可以被理解为“数据点到均值点的平均距离”。虽然这一描述在技术上和数学定义上都不严谨，但却有助于我们理解标准差的含义。计算标准差的公式可以被拆分为以下步骤：

1. 计算数据的均值；
2. 计算数据集中每一个值和均值的差，并将其平方；
3. 计算第2步的平均值，得到方差；
4. 对第3步得到的值开平方，得到标准差。

注意，以上每一步计算的均值都是算术平均值。

以温度数据集为例，我们使用Python计算数据集的标准差。

import numpy
temps=[31,32,32,31,28,29,31,38,32,31,30,29,30,31,26]
mean=numpy.mean(temps)  #==30.73
squared_differences=[]

for temperature in temps:
    difference=temperature-mean
    #how far is the point from the mean
    squared_difference=difference**2
    #square the difference
    squared_differences.append(squared_difference)
    #add it to our list
    average_squared_difference=numpy.mean(squared_differences)
    #This number is also called the "Variance"
standard_deviation=numpy.sqrt(average_squared_difference)
#We did it!
print(standard_deviation)   #==2.5157

通过以上代码，我们计算出数据集的标准差是2.5左右。这意味着平均来看，每一个数据点和平均温度31℉（-0.56℃）之间的距离是2.5℉（相当于1.38℃）。因此，冰箱温度在未来将下降至29℉（-1.67℃）以下。

计算标准差时，没有直接使用数据点和平均值的差，而是将差值平方后使用。这样做是为了突出离群值（outliers）——那些明显远离平均值的数据点。

变差尺度非常清晰地描述了数据的离散程度。当我们需要关心数据范围和波动情况时，这一指标显得尤为重要。

定距尺度和下一尺度之间的区别并不是十分明显。定距尺度数据没有自然的起始点或者自然的零点。比如，零摄氏度并不意味着没有温度。

2.6.4 定比尺度

定比尺度支持的数学运算在4个尺度中最全面和强大。除了之前提到的排序和减法之外，定比尺度支持使用乘法和除法。

案例

由于华氏度和摄氏度缺少自然零点，因此属于定距尺度。开氏温度却自豪地拥有自然零点。开氏温标为0时意味着没有任何热量，不随人为因素改变，我们可以有科学依据地说200开氏温度是100开氏温度的两倍。

银行账户金额也是定比尺度。“银行账户金额为0”和“2万美金是1万美金的两倍”这两种说法都是成立的。

测度中心

算术平均值对定比尺度仍然有效，同时还增加一种叫**几何平均值（geometric mean）**的新均值类型。后者在定比类型中并不经常使用，但仍然值得提及，它是指n个观察值连乘积的n次方根。

比如，对于冰箱温度数据，我们可以通过以下方式计算几何平均值：

import numpy
temps=[31,32,32,31,28,29,31,38,32,31,30,29,30,31,26]

num_items=len(temps)
product=1
for temperature in temps:
    product*=temperature
geometric_mean=product**(1/num_items)
print(geometric_mean)
#==30.634

几何平均值非常接近之前计算的算术平均值和中位数。但是请记住，这种情况并不经常发生。我们会在后面的统计学章节中用更多篇幅做出解释。

定比尺度的几个问题

定比尺度有一个重要前提：定比尺度数据通常是非负数。

试想如果我们允许负数的存在，那么一些比率很可能丧失含义。比如在银行账户案例中，假设允许账户金额为负数，那么以下比率将不具有任何意义：

$50000/-$50000=-1

`python
import numpy
temps=[31,32,32,31,28,29,31,38,32,31,30,29,30,31,26]

num_items=len(temps)
product=1
for temperature in temps:
product*=temperature
geometric_mean=product**(1/num_items)
print(geometric_mean)
#==30.634

几何平均值非常接近之前计算的算术平均值和中位数。但是请记住，这种情况并不经常发生。我们会在后面的统计学章节中用更多篇幅做出解释。

##### 定比尺度的几个问题

定比尺度有一个重要前提：**定比尺度数据通常是非负数**。

试想如果我们允许负数的存在，那么一些比率很可能丧失含义。比如在银行账户案例中，假设允许账户金额为负数，那么以下比率将不具有任何意义：

$50000/-\$50000=-1