提示：日出有盼，落日有念，心有所期，忙而不茫

---

前言

这里主要是根据王道考研视频所作的第二章，这一章主要探讨两个问题，数据如何再计算机中表示?，运算器如何实现数据的算数，逻辑运算？

---

提示：以下是本篇文章正文内容，下面案例可供参考

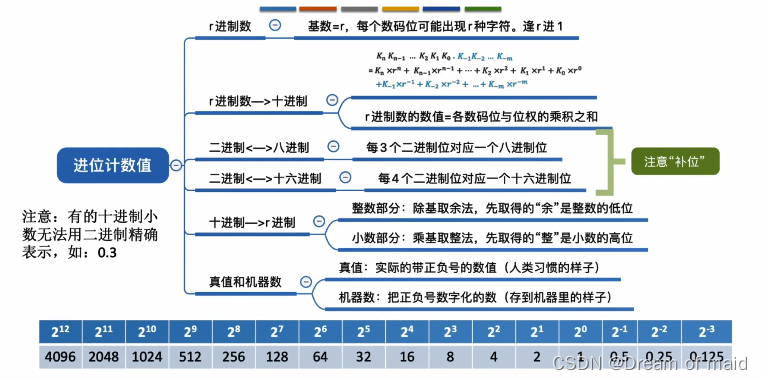
2.1.1 进位计数制

任意进制转化十进制
二进制转化为八进制
三个二进制数正好可以表示八种不同的状态
以小数点开始左右3位为一组，每组转化为对应的八进制符号（高位整数补零，地位小数补零）

二进制转化为十六进制
四个二进制数正好可以表示十六种不同的状态
以小数点开始左右4位为一组，每组转化为对应的16进制符号

八进制转化二进制

十六进制转化为二进制

进制的常见书写方式
二进制以B结尾，八进制以O开头，十六进制以H结尾或者以0x开头，十进制以D结尾

十进制转化为任意进制

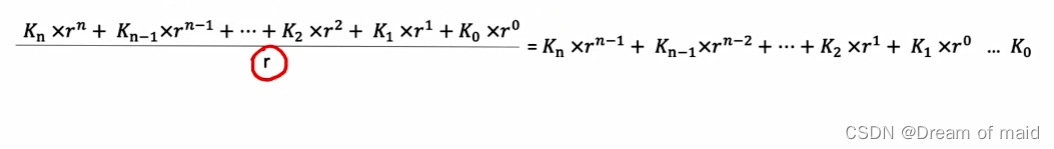
方法一
(除基取余法整数部分)：任意一个整数都可以写成整数X(R的一次方，二次方，一直到n-1次方，所以是可以整除的)部分加上余数K0(0~R)部分 ，所以我们除以R之后得到余数K0便是R的零次方上的数值,再用得到的商再除以R得到的便是K1（先取得的余是整数的低位）

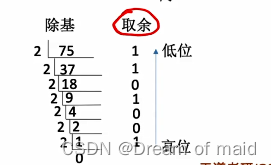
（乘基取整法小数部分）：核心思想也是一样 想办法把K-1算出来，这里发现乘上一个R便可直观的得到K-1的值 ，得到的结果再乘R得到的便是K-2的值（先取得的整是小数的高位）

方法二（拼凑法）
若是给你的十进制数不是特别大的话，可能使用这些拼拼凑凑的方法可能要快一些，假如要将十进制转化成八进制，完全可以先转化成二进制，然后二进制再三位一组转化为八进制
小结回顾

2.1.2 BCD码

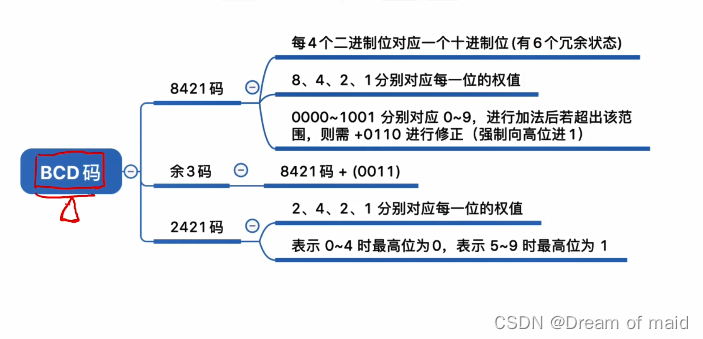
BCD:用二进制编码的十进制
8421码
通过上述我们知道要想表示0~9这十个数，必须最少需要4bit,而4bit则可以表示16个值 ，这样也就会有6个yong余，8421码的提出便是为了快速转换
8421码的相加：若是两个数对应的8421码相加的结果不在映射表中，也就是落到了10~15这个区间这个时候我们再加上6 这样就一定会向高位进一个1，而低位所留下的部分又正好是我们个位所留下的部分

余3码
也就是在8421码的基础上加上一个0011得到不同的映射关系，
2421码
我们依然是使用四个二进制位来表示一个十进制位，不过这四个的权值是2421，同样需要注意0 ~ 4第一位都是零，5 ~ 9第一位则一定是1 这也是为了避免同一个值有不同的2421码（如5 0101或1011）

回顾

2.1.3 无符号整数的表示和运算

这里主要探讨两个问题，无符号整数，在计算机硬件内，如何表示，无符号整数的加法，减法运算时怎么用硬件实现的
机器字长限定了每一次只能进行几个bit运算，机器字长也限制了通用寄存器只能有多少位
无符号整数
全部二进制位都是数值位，没有符号位，第i位的位权是 2的i-1次方，n bit无符号整数表示的范围0~2的n次方-1 超出则溢出，意味着计算机无法一次处理这么多，可以表示的最小的数全是0，可以表示的最大的数全是1
无符号整数的减法运算
被减数不变，减数全部按位取反，末位+1 减法变加法，从最低为开始，按位相加，并往最高位进位

知识点回顾

2.1.4 带符号整数的表示和运算(原反补)

首先我们这节主要解决的是带符号整数，在计算机硬件内，如何表示，第二带符号整数的加法，减法运算是如何用硬件实现的？
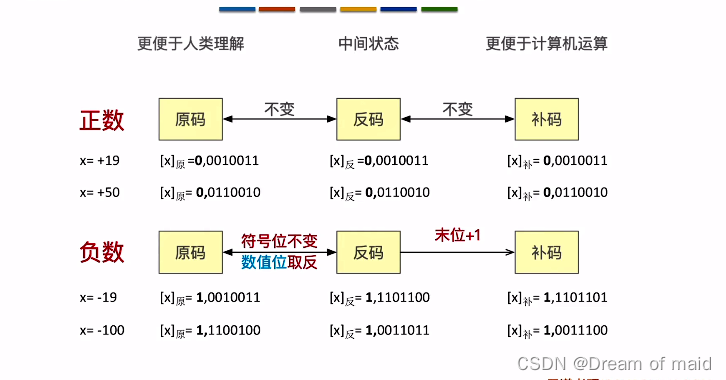
同一个带符号整数可以用不同的编码方式表示 ，这便是原码 补码 反码，形式不同但是含义相同
原码表示法
分为符号位和数值位 符号位0正1负 其实也就是之前的表示方式，不过是使用一位来表示正负，其他的依然如之前的表示，注意这里假设的机器字长是n+1

原码的缺点：符号位不能参与运算，需要设计复杂的硬件电路才能处理，所以聪明的科学家也就想到了用补码来表示真值——符号位可以参与运算（正数的补码可以解释为位权，负数的补码不能解释为位权）

• 方法 一*
  正数的原码，反码，补码都是不变的
  负数的原码到反码是符号位不变，数值位取反，然后末位+1得到补码
  若是让你根据补码来求反码，你可以先求原码再求反码（这里使用的方式是第二种，从右往左找到第一个1 这个1左边的所有数值位按位取反便可得到原码）
  

方法二
从右往左找到第一个1，这个1左边的所有“数值位”按位取反（按照之前我们计算机计算的方法，把所有的数值位按位取反，末位加一个一，若是反码最后一个是一，并且这个一前面也是一，就会导致不断的向前进位，直到前面那个是零才会停止，也就导致从右往左第一个1的右边的值与原码是一致的，所以这也就是为什么我们从右往左找到第一个1，这个1左边的所有数值按位取反便可得到补码）

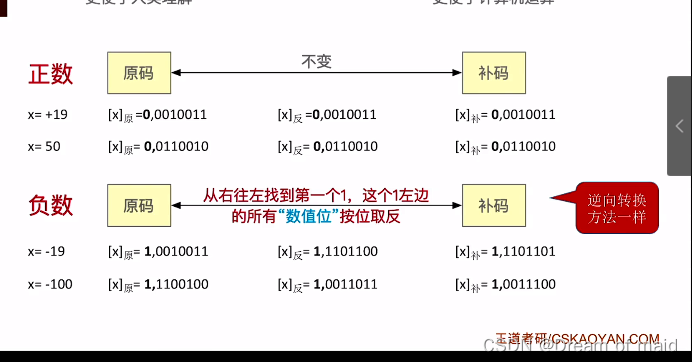
方法一是计算机处理的方式，我们若是手算的话 推荐第二种
带符号整数加法运算
从低位开始，按位相加（符号位参与运算），并往更高位 进位

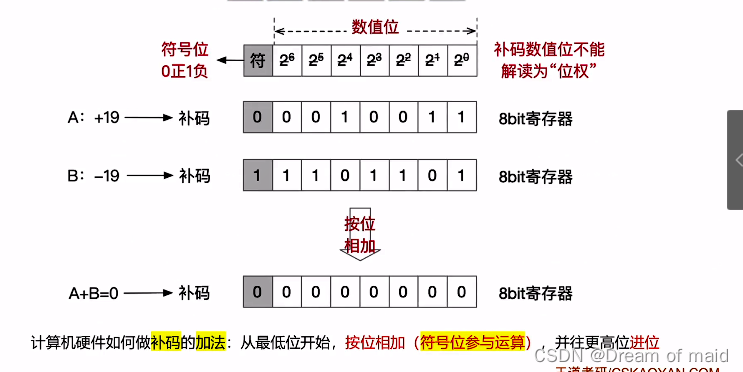
带符号整数减法运算
A-B=A+(-B),也就是将减数取负值，所以也就有了全部位取反
方法一：首先是全部位按位取反，然后末位加一，与上面负数求补码有所不同（符号位不变，数值位取反）
方法二：与之前类似，从右往左找到第一个1，此1左边的全部取反（之前负数求补码是数值位取反，这里是全部），右边的不变便可得到原码或者补码

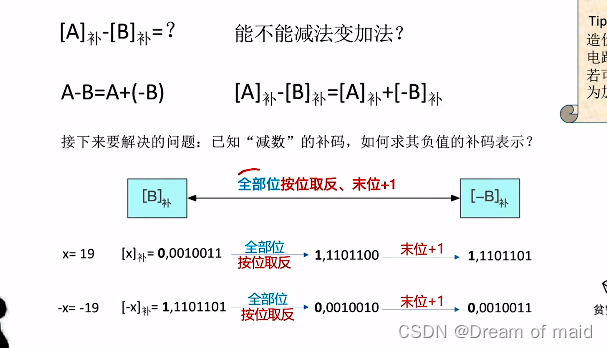
这也就能和之前的无符号的减法相联系，减数 全部取反，末位加1，相联系
知识点回顾

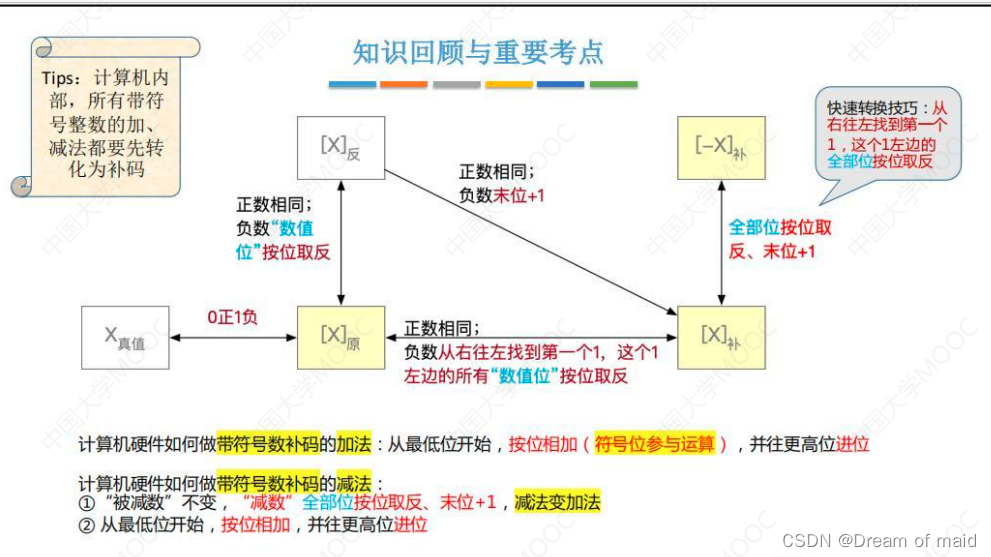
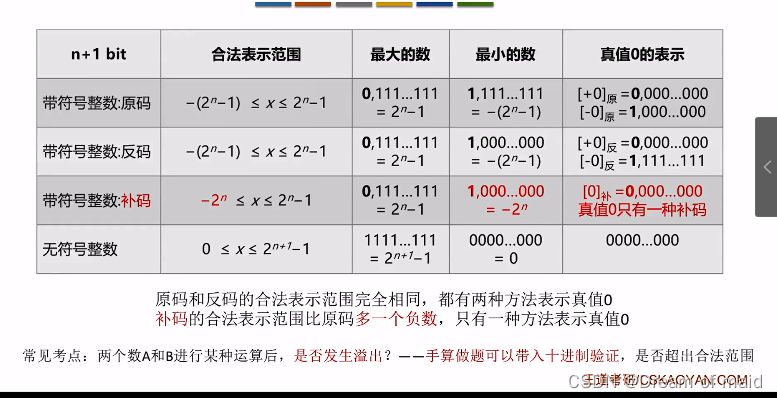
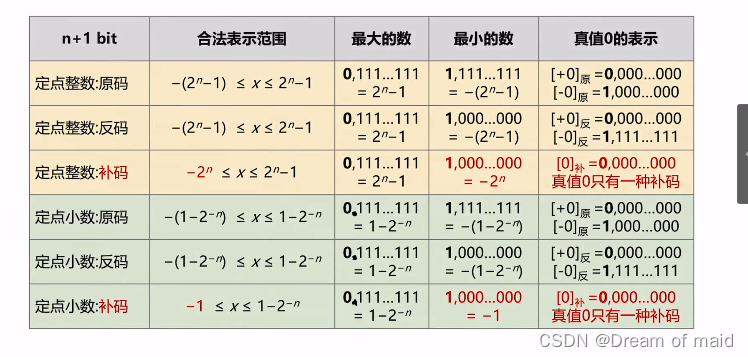
2.1.5原反补码的特性对比

注意加红的即可，如若是-64-64 结果保存在原码中则会溢出，若是保存于补码中则不会溢出

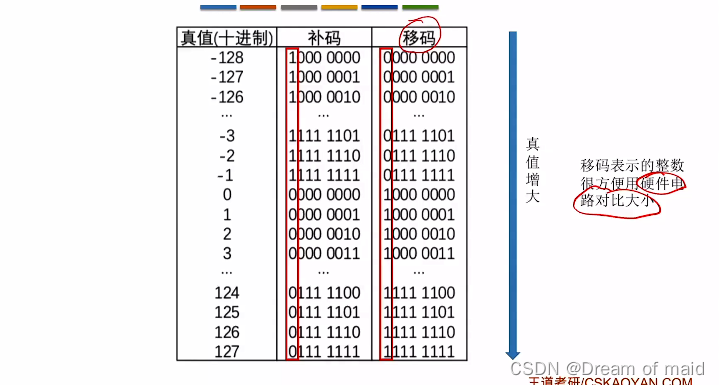
2.1.6 移码

补码的基础上将符号位取反

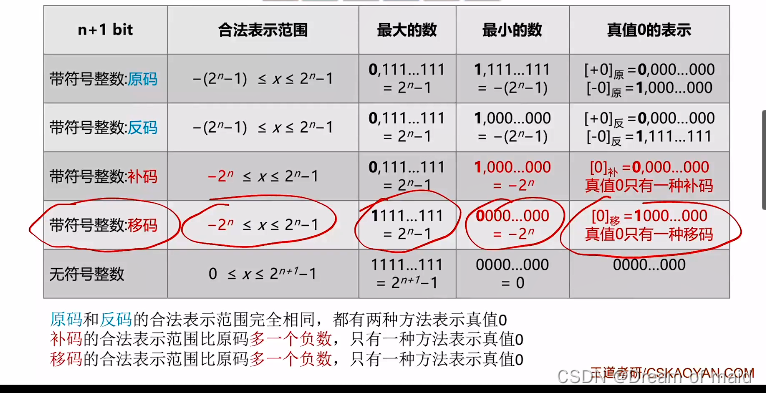
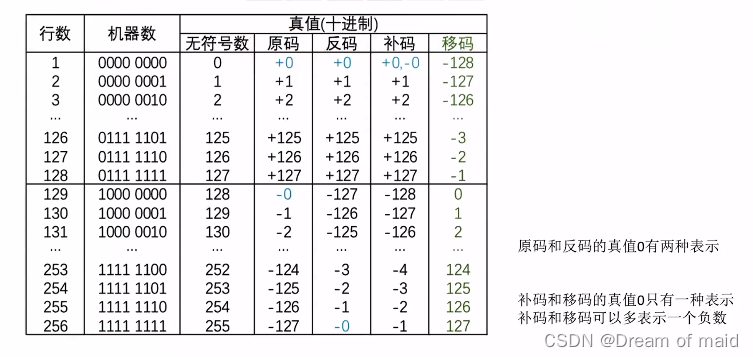
2.1.7 定点小数

反码，补码和上面是一样的 这里看一下区别

另外一个需要注意的地方就是取值范围以及最小的数，还有真值零的表示