目录
- 0.排序
- 思维导图(总)
- 一、插入排序
- 1.直接插入排序
- 思路分析
- 代码实现
- 时间复杂度
- 2.希尔排序
- 思路分析
- 代码实现
- 时间复杂度
- 二、选择排序
- 1.选择排序
- 思路分析
- 代码实现
- 时间复杂度
- 2.堆排序
- 思路分析
- 代码实现
- 时间复杂度
- 三、交换排序
- 冒泡排序
- 思路分析
- 代码实现
- 时间复杂度
0.排序
// Sort.h
#pragma once
#include <stdio.h>
#include <assert.h>
#include <stdlib.h>
#include <time.h>
#include "Stack.h"
// 插入排序
void InsertSort(int* a, int n);
// 希尔排序
void ShellSort(int* a, int n);
// 选择排序
void SelectSort(int* a, int n);
// 堆排序
void AdjustDwon(int* a, int n, int root);
void HeapSort(int* a, int n);
// 冒泡排序
void BubbleSort(int* a, int n);
思维导图(总)

一、插入排序
1.直接插入排序
思路分析
-
升序排序
-
一个数插入一个升序列,找到不比自己大的数,插入在这个数的后面

-
具体是如何插入的:
- 如下图,如果 a[end]>tmp 就往后挪动数据→a[end+1]=a[end],当找到 不比tmp大的数 之后,将tmp插入到这个数的后面→a[end+1]=tmp

- 如下图,如果 a[end]>tmp 就往后挪动数据→a[end+1]=a[end],当找到 不比tmp大的数 之后,将tmp插入到这个数的后面→a[end+1]=tmp
-
因此,对于一个无序列,就是依次插入数据

代码实现
// 插入排序
void InsertSort(int* a, int n)
{
assert(a);
for (int i = 1; i < n; i++)
{
int tmp = a[i];
int end = i - 1;
while (end >= 0)
{
if (a[end] <= tmp)
{
break;
}
a[end + 1] = a[end--];
}
a[end + 1] = tmp;
}
}
时间复杂度
- 最坏的情况:排升序,但原数列为降序
array[0]挪动数据并插入的次数为:0;
array[1]挪动数据并插入的次数为:1;
array[2]挪动数据并插入的次数为:2;
array[3]挪动数据并插入的次数为:3;
…………
array[n]挪动数据并插入的次数为:n;
Σ = 0+1+2+3+……+n = (1+n)*n/2
∴ 时间复杂度O(N)=N²
- 最好的情况:时间复杂度O(N)=N
插入排序的适应性很强,对于有序、局部有序的情况,都能效率提升
2.希尔排序
思路分析
为了优化直接插入,我们选择进行预排序,让较大的位于前列的数先排到较后面的位置,以此减少挪动数据的次数

预排序:分组,每组进行插入排序
下图以gap==3为例


gap的变化:
while(gap)
{
int gap = n / 2;
gap /= 2;
}
//当gap==1时就是直接插入排序
//or
while(gap)
{
int gap = n / 3;
gap = (gap/3 + 1);
}
代码实现
// 希尔排序
void ShellSort(int* a, int n)
{
assert(a);
int gap = n / 2;
while (gap)
{
for (int i = 1; i < n; i++)
{
int tmp = a[i];
int end = i - gap;
while (end >= 0)
{
if (a[end] <= tmp)
{
break;
}
a[end + gap] = a[end];
end -= gap;
}
a[end + gap] = tmp;
}
gap /= 2;
}
}
时间复杂度
希尔排序的时间复杂度算起来很复杂,预排序之后无法确定数列的顺序情况。
这里直接给结果:O(N)=N^1.3
二、选择排序
1.选择排序
思路分析
遍历数组(以排升序为例)
找到最一小的数与数组第一个位置的数交换;
找到第二小的数与数组第二个位置的数交换;
……(依次类推)

优化:两头缩进
从数组的头和尾开始,在中间(区间为👉[begin,end])同时找最大和最小的数,找到分别与“两头的数”交换,依次类推,“两头缩进”

找到后 Swap ↓
Swap(&a[begin], &a[mini]);
Swap(&a[end], &a[maxi]);
++begin;
--end;
- 注意!:Swap之后:
begin → min ; mini → original-a[begin]- 如果 original-a[begin] → max 则会影响 a[maxi] =? max
if (begin == maxi)即如果原本 begin 指向的数是 max,则 Swap 之后这个数已经被交换到了 mini 所指向的位置 - end 指向的数是否改变不影响,因为,我们只是要把 max 放在最后面的位置(同时保持数据不丢失)
- 就是说 ,begin 代表头部的位置,end 代表尾部的位置;mini 是最小值的下标,maxi 是最大值的下标
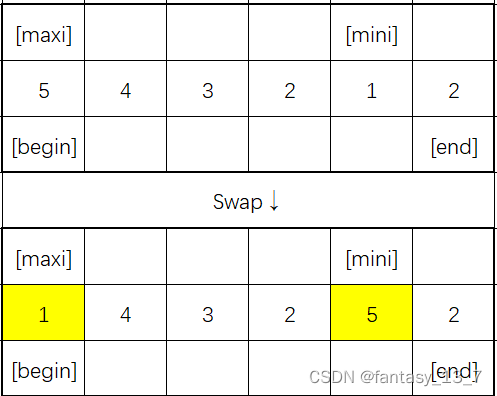
- 如果 original-a[begin] → max 则会影响 a[maxi] =? max
代码实现
//优化后:
void Swap(int* x, int* y)
{
assert(x && y);
int tmp = *x;
*x = *y;
*y = tmp;
}
// 选择排序
void SelectSort(int* a, int n)
{
assert(a);
int begin = 0, end = n - 1;
while (begin < end)
{
int mini = begin, maxi = end;
//[begin+1,end-1]
for (int j = begin; j <= end; j++)
{
if (a[j] < a[mini])
mini = j;
if (a[j] > a[maxi])
maxi = j;
}
//swap之前 min==a[mini] max==a[maxi]
Swap(&a[begin], &a[mini]);
//swap之后:begin → min ; mini → original-a[begin]
//if(original-a[begin] → max)则会影响 a[maxi] =? max
if (begin == maxi)//如果原本begin指向的数是max,则swap之后这个数已经被交换到了mini所指向的位置
maxi = mini;
Swap(&a[end], &a[maxi]);
++begin;
--end;
}
}
时间复杂度
未优化的算法:
从头找到尾
找到最一小的数与数组第一个位置的数交换,查找的次数为:n - 1;
找到第二小的数与数组第二个位置的数交换,查找的次数为:n - 2;
…………
最后一次查找次数为:1( n -(n-1))
Σ = 1+2+3+……+(n-1)= n*(n-1)/2
∴ 时间复杂度为O(N²)
2.堆排序
详细分析过程见→二叉树-堆| [堆的实现【建堆算法图解+分析】]
思路分析
排升序:建大堆。把数组按大堆的方式排列,此时堆顶就是最大的数,让堆顶与数组最后一个数交换,最大的数就被放在了数组的尾部。对于前面的部分,调整使其依旧为大堆,此时堆顶的数就是第二大的数……重复这个操作👉向下调整建堆,不断取堆顶的数
排降序:建小堆。思路同上。
代码实现
// 堆排序
void AdjustDwon(int* a, int n, int root)
{
assert(a);
int parent = root;
int child = parent * 2 + 1;
while (child < n)
{
if ((child + 1) < n && a[child + 1] > a[child])
++child;
if (a[parent] < a[child])
Swap(&a[parent], &a[child]);
else
break;
parent = child;
child = parent * 2 + 1;
}
}
void HeapSort(int* a, int n)
{
assert(a);
//建大堆
for (int parent = (n - 1 - 1) / 2; parent >= 0; parent--)
{
AdjustDwon(a, n, parent);
}
//取堆顶的数据并向下调整
int end = n - 1;
while (end)
{
Swap(&a[0], &a[end]);
AdjustDwon(a, end, 0);
end--;
}
}
时间复杂度
向下调整建堆的时间复杂度:O(N)
取堆顶数据然后向下调整时间复杂度:O(logN) → 重复 N次 → O(N*logN)
∴ 时间复杂度 为 O(N*logN)
三、交换排序
冒泡排序
思路分析
前后比较交换
以下列这个数组为例,展示一趟冒泡排序:


代码实现
// 冒泡排序
void BubbleSort(int* a, int n)
{
assert(a);
for (int j = 0; j < n; j++)
{
for (int i = 0; i < n - j - 1; i++)
{
if (a[i] > a[i + 1])
Swap(&a[i], &a[i + 1]);
}
}
}
时间复杂度
第一趟冒泡排序:n-1次
第二趟冒泡排序:n-2次
……
第n趟冒泡排序:n-n次
Σ = 1 + 2 + 3 + …… + n-1 = n(n-1)/2
∴时间复杂度为O(N)=N²