线段树

线段树是一种二叉树，通俗易懂的来说就是对于一个线段，我们会用一个二叉树来表示。线段树是一种工具，她能把对区间（线段）的修改与维护从0(N)的时间复杂度变成0(logN)。

如图：

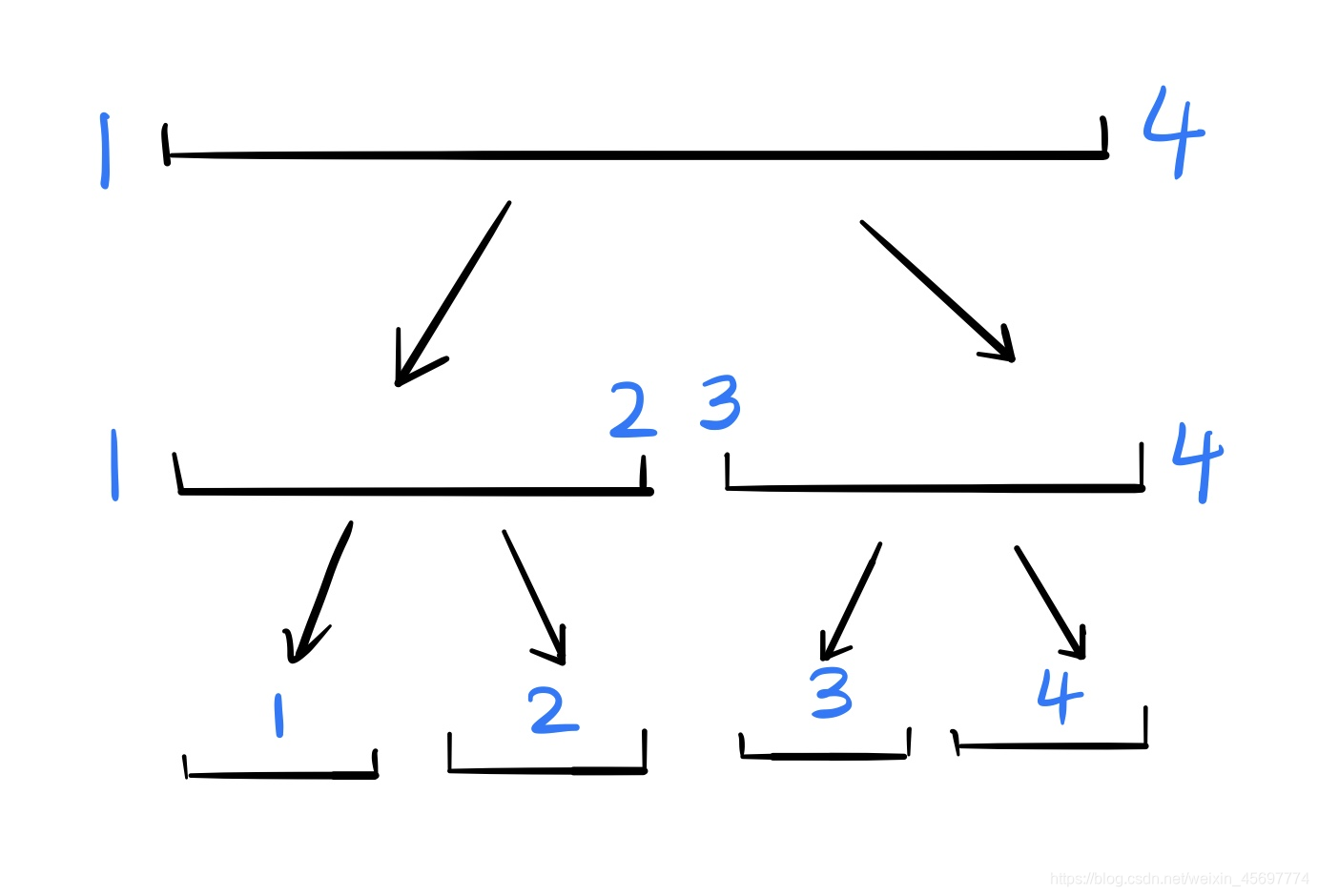
 如上图，我们可以得到一个性质：节点i的权值=她的左孩子的权值+她的右孩子的权值。

 我们知道，一颗从1开始编号的二叉树，节点i的左孩子和右孩子的编号分别是2*i和2*i+1.

 当我们建立一颗线段树时，我们设一个结构体，她一般需要包含三个元素，一个左子树下标，一个右子树下标，还有一个表示这个节点表示的线段和。

建树代码如下：

void build(int i,int l,int r)
tree[i].l=l;tree[i].r=r;
if(l==r)//如果这个节点是叶子节点
{
tree[i].sum=l;
return ;
}
int mid=(l+r)>>1;
build(i*2,l,mid);
build(i*2+1,mid+1,r);
tree[i].sum=tree[i*2].sum+tree[[i*2+1].sum;
}

 需要注意的是我们在构建一颗线段树时，可能需要开好几倍的内存去存储。 

前面说了，线段树的主要功能是对区间进行维护和修改，既然要进行以上的两种操作那肯定要先对这棵树进行查询，在这里我先给出查找某一段区间和的查询方法：

1.查询从根节点开始，依次向下查询

2.如果查询到的这个区间完全包括在要查询的目标区间里面，那么直接返回这个区间的值。

3.如果这个区间的左儿子和要查询的左儿子有交集，那么搜索左儿子。

4.如果这个区间的右儿子和要查询的左儿子有交集，那么搜索右儿子。

5.将搜索到的值依次返回即可。

    int search(int i,int l,int r){
    if(tree[i].l>=l && tree[i].r<=r) 
        return tree[i].sum;
    if(tree[i].r<l || tree[i].l>r)  return 0; 
    int s=0;
    if(tree[i*2].r>=l)  s+=search(i*2,l,r); 
    if(tree[i*2+1].l<=r)  s+=search(i*2+1,l,r); 
    return s;
}

今天只大概了解了线段树的一部分，剩下的明天再深入学习。 

https://blog.csdn.net/weixin_65829986/article/details/130025091 

https://blog.csdn.net/weixin_65829986/article/details/130024647