一、什么是归并排序？

归并排序，是创建在归并操作上的一种有效的排序算法。算法是采用分治法（Divide and Conquer）的一个非常典型的应用，且各层分治递归可以同时进行。归并排序思路简单，速度仅次于快速排序，为稳定排序算法。

二、归并排序（递归）

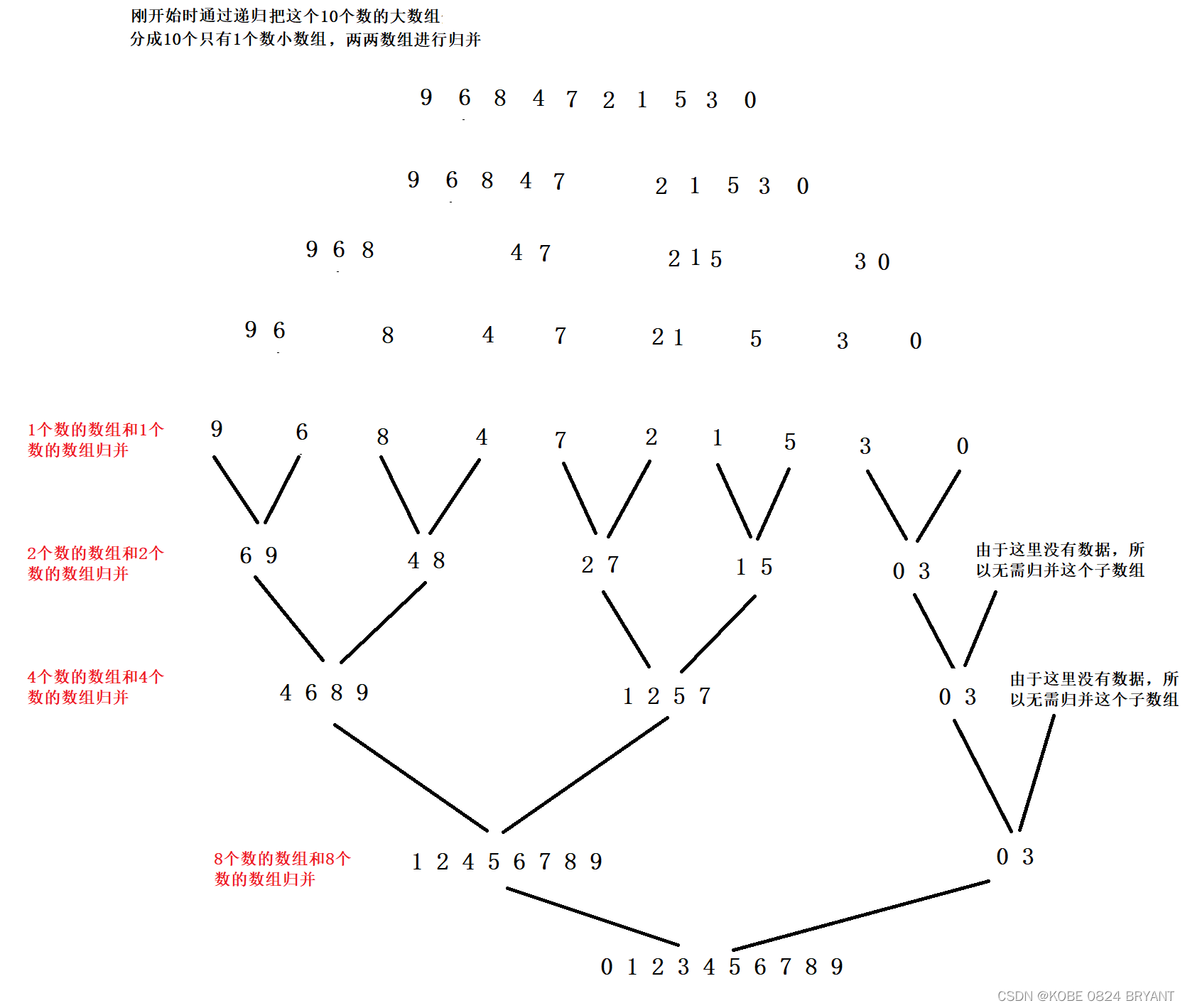
归并排序（递归）的基本思路：递归的思路很简单，就是把整个大数组用二分法逐步划分成小数组，直到数组只有一个数或者没有数的时候开始往回归并，归并就是用两个有序的数组遍历比较，哪个数小就把它归并到开辟的临时数组中去，这样就能把两个有序的数组归并成一个有序的数组，那归并得到的这个有序的数组再和另外一个有序的数组归并，以此类推，则最后一次就是把左右两半有序的数组进行归并从而使整个数组有序。
在这里插入图片描述
参考代码如下：


void _MergeSortR(int* a, int left, int right, int* tmp)
{
	//如果递归到小区间只有一个值(left==right)或者不存在(left>right)，则返回
	if (left >= right)
	{
		return;
	}
	
	//递归把需要排序的大区间逐步二分成小区间，直到区间只有
	//一个值或者区间不存在的时候再开始归并且回归
	int mid = (left + right) / 2;
	_MergeSortR(a, left, mid, tmp);
	_MergeSortR(a, mid + 1, right, tmp);

	//来到这的时候说明区间只有一个值或者区间不存在了，开始归并
	int begin1 = left;
	int end1 = mid;
	int begin2 = mid + 1;
	int end2 = right;

	//两个小数组归并时把数据归并到开辟的临时数组tmp中，从left位置开始放，
	//方便归并完数组的数据之后把tmp数据拷贝回到原数组中
	int i = left;

	//当两个小数组都还有数据就继续归并，直到某一个小数组没有数据了就停止
	while (begin1 <= end1 && begin2 <= end2)
	{
		//哪个数据小就把它归并到tmp对应的位置上去(升序)
		if (a[begin1] <= a[begin2])
		{
			tmp[i++] = a[begin1++];
		}
		else
		{
			tmp[i++] = a[begin2++];
		}
	}
	//来到这的时候一定有一个小数组已经归并完了，但是是左边那个还是右边那个
	//是不知道的，那么我们不妨写下两个循环，如果是右边走完了，那就进入第一个
	//循环，把剩下的数据逐一放到tmp数组中去，否则就进入第一个循环
	while (begin1 <= end1)
	{
		tmp[i++] = a[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[i++] = a[begin2++];
	}

	//最后把这归并到tmp中对应位置的数据拷贝回原数组中，注意要
	//小心地控制边界，tmp是从left位置开始的，所以是tmp+left
	//同理，拷贝数据回原数组也是要放到a+left的位置上去的，元素个数
	//是right-left+1个，因为这个是左闭右闭区间，最后需要+1才是元素个数
	//例如，[0,9]的下标是有9-0+1个元素的
	memcpy(a + left, tmp + left, sizeof(int) * (right - left + 1));
}

void MergeSortR(int* a, int n)
{
	assert(a);
	//开辟一个临时数组用于存放归并时的数据
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("");
		return;
	}

	_MergeSortR(a, 0, n - 1, tmp);

	free(tmp);
	tmp = NULL;
}

递归动图：
在这里插入图片描述

时间复杂度：由代码可知，这里的递归运用的是二分法，所以需要递归logN层，在每一层归并子数组时，都需要遍历一次整个数组，所以每一次归并时比较次数时O(N)，所以毫无疑问，归并排序递归法的时间复杂度为O(N*logN)，空间复杂度为O(N)，因为开辟了一个临时数组。

三、归并排序（非递归）

由于递归排序终究需要不断地开辟栈帧，当数据量很大的时候递归深度会很大，所以我们有必要学会用非递归排序的方法代替递归排序。那么如何把归并排序的递归版本改写成非递归呢？接下来我们探讨一下。
可以看到，归并排序的递归是把整个大数组逐步二分成小数组，直到每个小数组的元素个数是一个或者没有的时候才开始回归归并的，而且两个数组能够归并的前提条件是它们都是有序的，所以我们不能直接把大数组分成两个小数组直接归并，因为数组的两边不一定是有序的，那么我们可以反过来归并，直接从1个数和1个数归并（因为一个数的数组可以认为是有序的）开始，然后再2个数和2个数归并，再到4个数和4个数归并，以此类推，直到最后一次大数组的左右两边都有序了，那么再归并一次就能使整个数组有序了。
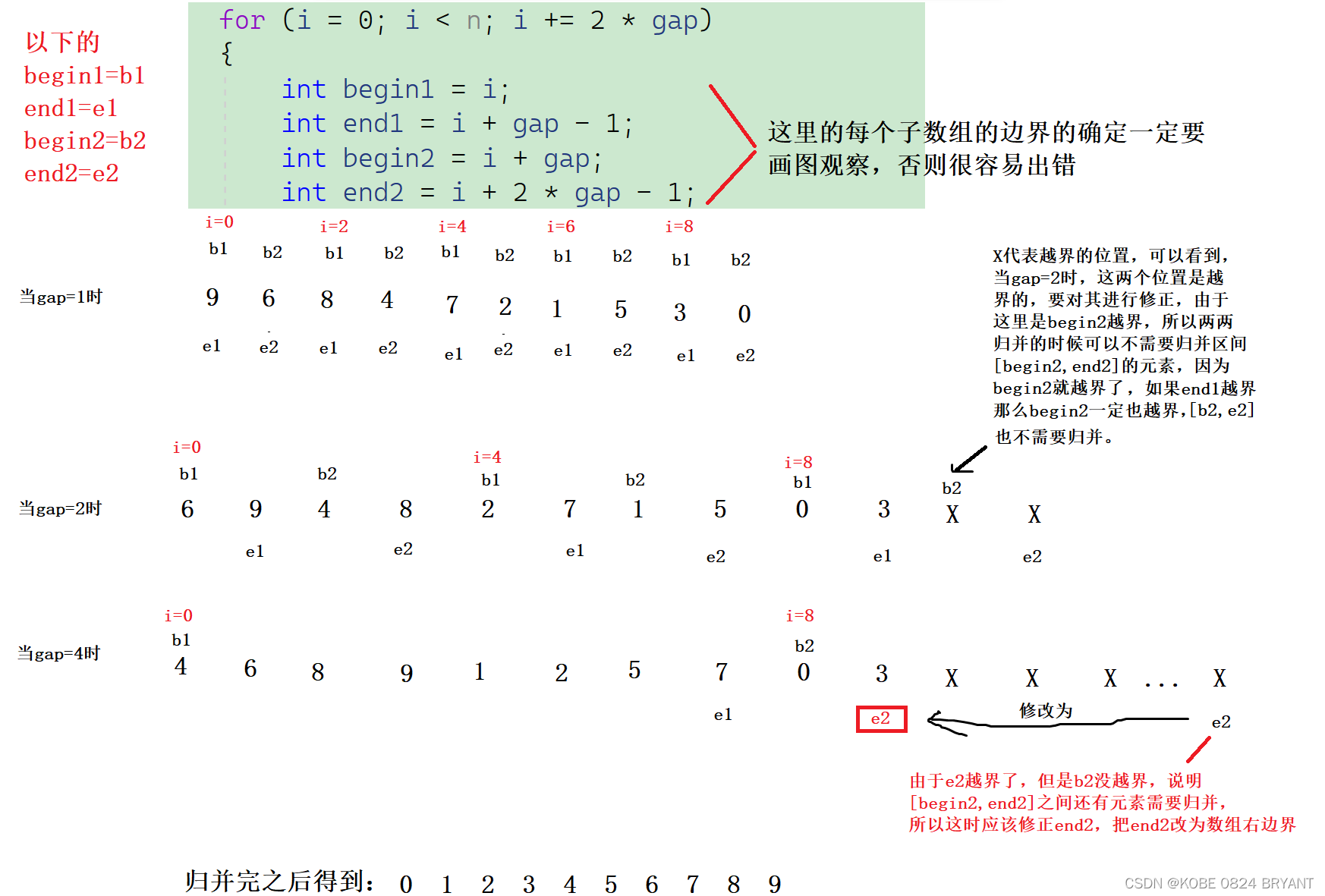
递归可以只加一个判断条件就能控制住边界越界的问题，当left>=right就直接返回就控制住了，而循环无法完成类似操作，所以只能自己在每一次归并的时候检查边界值是否越界，如果有越界就加以修正。在这里控制边界才是归并排序非递归的最核心的地方，稍有不慎，就会导致程序崩溃了。

具体操作如下图：
在这里插入图片描述
参考代码如下：

void MergeSortNonR(int* a, int n)
{
	assert(a);
	//开辟一个临时数组用于存放归并时的数据
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("");
		return;
	}

	//gap代表每个小数组有多少个元素
	int gap = 1;
	//每一组的元素个数当然不能大于等于数组本身的大小了
	while (gap < n)
	{
		int i = 0;
		//第一次进来，gap==1，那么就是一一归并
		for (i = 0; i < n; i += 2 * gap)
		{
			//这里边界的确定请参考上面图片
			int begin1 = i;
			int end1 = i + gap - 1;
			int begin2 = i + gap;
			int end2 = i + 2 * gap - 1;
			//当数组的元素个数不是2的整数倍时，end1，begin2，end2都
			//有可能存在越界，所以需要判断和修正边界值
			//如果end1或者begin2越界了，其实只需要判断begin2是否越界也就行了，
			//因为end1越界那么begin2一定也越界的，那么归并时[begin2,end2]
			//就没有数据了，也就没有和[begin1,end1]元素归并的必要了，直接break
			//进入下一次循环
			if (end1 >= n || begin2 >= n)
			{
				break;
			}
			//如果end2>=n越界，那么说明[begin2,end2]中还有元素需要归并，所以
			//修正以下end2，使end指向数组中最后一个元素即可，再和[begin1,end1]
			//中的元素进行归并
			else if (end2 >= n)
			{
				end2 = n - 1;
			}
			//谨记：这里不能写成else，因为下面的步骤是必须执行的

			//以下就是归并的步骤了，和递归的写法是一样的
			int j = begin1;
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] <= a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				else
				{
					tmp[j++] = a[begin2++];
				}
			}
			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}
			/*int k = 0;
			for (k = i; k <= end2; k++)
			{
				a[k] = tmp[k];
			}*/

			//这里的边界控制也要注意，不能写成a+begin1、tmp+begin1和
			//end2-begin1+1，因为begin1已经再归并的时候改变了
			memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));

		}//end of for

		//一一归并完了之后就是两两归并，然后四四归并，所以这里是gap*=2
		gap *= 2;
	}

	free(tmp);
	tmp = NULL;
}