C++回溯算法---图的m着色问题

图的m着色问题是指给定一个图以及m种不同的颜色，尝试将每个节点涂上其中一种颜色，使得相邻的节点颜色不相同。这个问题可以转化为在解空间树中寻找可行解的问题，其中每个分支结点都有m个儿子结点，最底层有m的n次方个叶子结点。算法的思路是在解空间树中做深度优先搜索，并使用约束条件来剪枝优化搜索。

代码：

#include <iostream>
#include <cstring>
/*
*   图的m着色问题
*/
using namespace std;

const int maxn = 1005;
int G[maxn][maxn], color[maxn];//用于存储图中的边--用于存储每个节点的颜色 
int n, m; //n表示图中节点的数量，m表示可供选择的颜色数目。

bool ok(int u, int c) {
    for (int i = 1; i <= n; i++) {
        if (G[u][i] == 1 && color[i] == c)
            return false;
    }
    return true;
}

bool dfs(int u) {
    if (u > n)
        return true;
    for (int i = 1; i <= m; i++) {
        if (ok(u, i)) {
            color[u] = i;
            if (dfs(u + 1))
                return true;
            color[u] = 0;
        }
    }
    return false;
}

int main() {
    memset(G, 0, sizeof(G));//初始化邻接矩阵为0
    memset(color, 0, sizeof(color));//初始化颜色为0
    int e;//e表示图中边的数量
    cin >> n >> e >> m;
    for (int i = 0; i < e; i++) {
        int u, v;
        cin >> u >> v;
        G[u][v] = G[v][u] = 1;
    }

    if (dfs(1)) {
        cout << "Yes" << endl;
        for (int i = 1; i <= n; i++) {
            cout << "结点 " << i << " 的颜色为： " << color[i] << endl;
        }
    }
    else {
        cout << "No" << endl;
    }

    return 0;
}

分析：

这个算法的实现包括两个主要步骤：

1. 判断颜色是否符合要求

对于每个节点 u，如果它与另一个节点 v 有边相连，且这两个节点颜色相同，那么就不能把节点 u 涂为该颜色。因此，需要定义一个函数 ok() 来判断某个节点染上某种颜色是否符合要求。具体来说，ok(u, c) 函数返回值为true表示节点 u 可以涂上颜色 c，否则返回false。

      2.使用深度优先搜索

使用深度优先搜索（DFS）从解空间树的根节点开始搜索，并在每个分支结点处调用 ok() 函数来剪枝。如果在整棵解空间树中找到了一组可行解，那么算法就停止搜索并输出结果。如果找不到任何一个可行解，则算法输出无解信息。

具体实现过程：

首先，需要定义一个二维数组 G[ ][ ]，用于存储图中的边。其中，G[u][v] == 1 表示节点 u 和节点 v 之间有边相连，反之为 0。同时，还需要定义一个一维数组 color[ ]，用于存储每个节点的颜色。

首先将所有边权赋值为 0，即不存在边。然后，读入所有边，将对应的边权赋值为 1。读入颜色数 m，并从节点 1 开始做深度优先搜索，依次尝试给每个节点涂上不同的颜色。在每个分支结点处，使用 ok() 函数来判断是否符合要求。如果染色成功，则继续对下一个节点做深度优先搜索。如果找到了一组可行解，则输出结果。

运行结果：

---

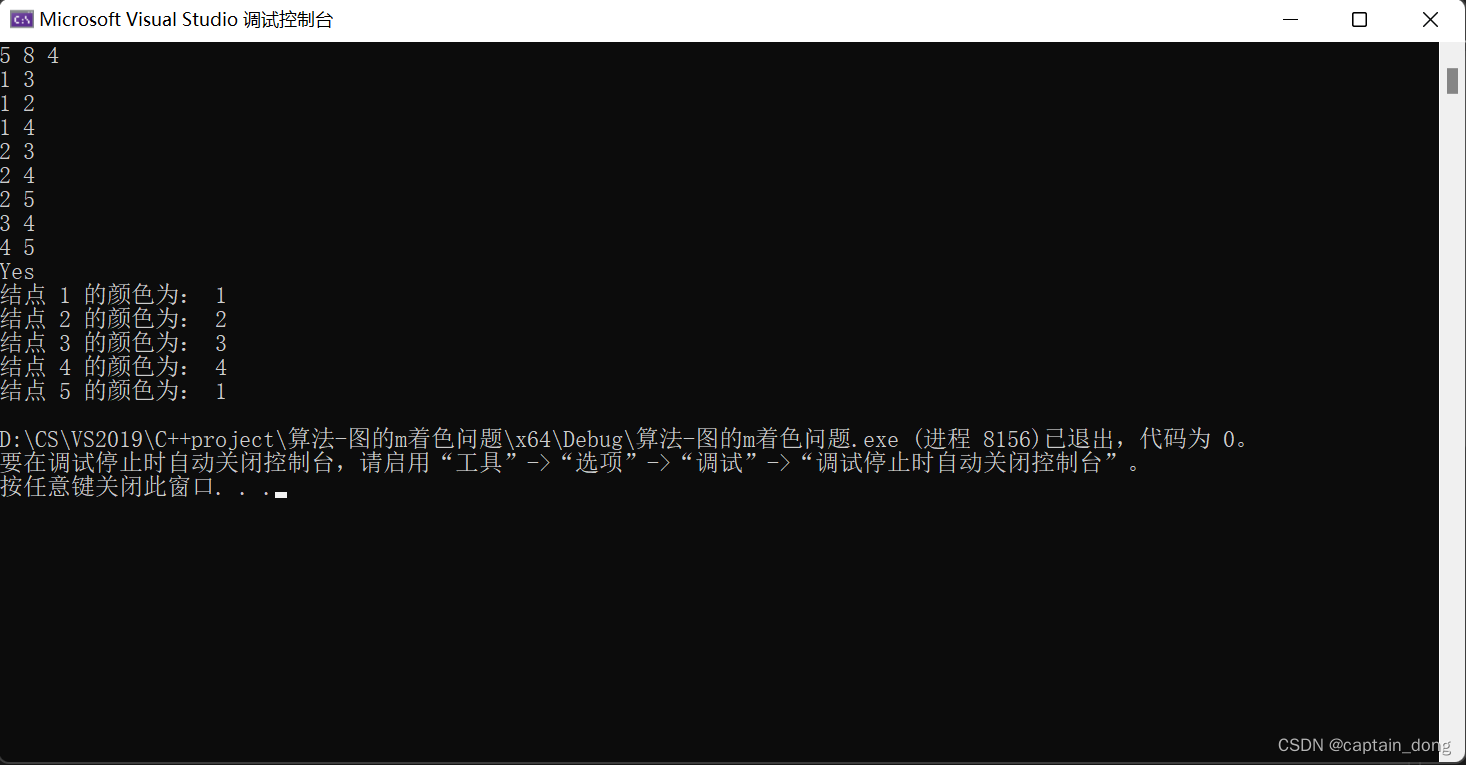
问题描述

 给定无向连通图G=(V, E)和m种不同的颜色，用这些颜色为图G的各顶点着色，每个顶点着一种颜色。是否有一种着色法使G中相邻的两个顶点有不同的颜色。这个问题是图的m可着色判定问题。若一个图最少需要m种颜色才能使图中每条边连接的两个顶点着不同颜色，则称这个数m为该图的色数。求一个图的色数m的问题称为图的m可着色优化问题。

例如：点个数n=7，颜色m=3的涂色方案

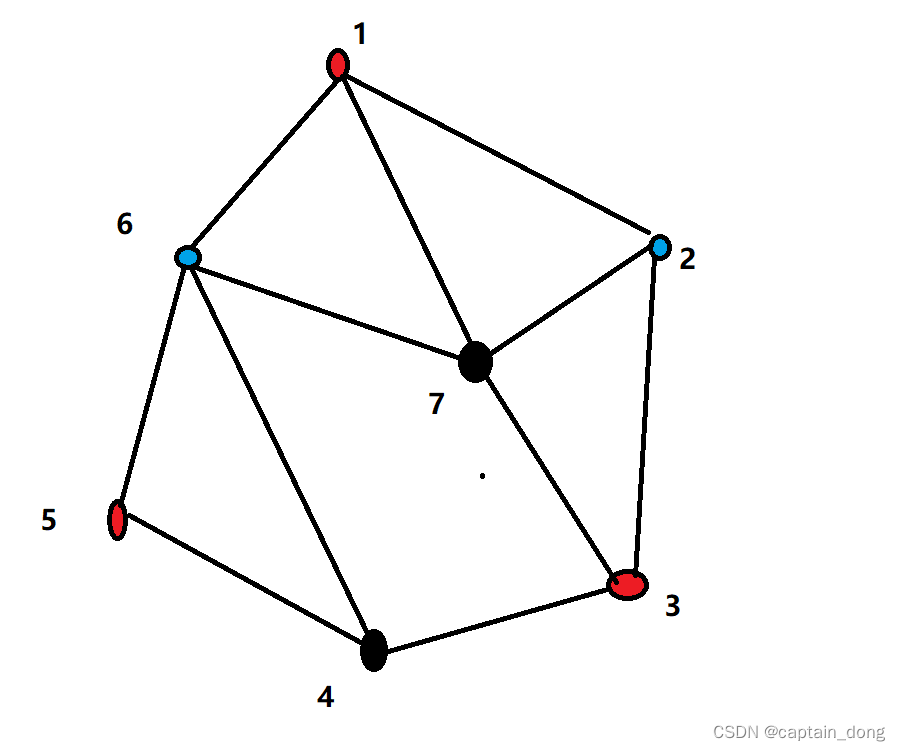
算法设计

 一般连通图的可着色问题，不仅限于可平面图。

 给定图G=（V，E）和m种颜色，如果该图不是m可着色，给出否定回答；若m可着色，找出所有不同着色方法。

算法思路
设图G=(V, E), |V|=n, 颜色数= m, 用邻接矩阵a表示G, 用整数1, 2…m来表示

m种不同的颜色。顶点i所着的颜色用x[i]表示。

问题的解向量可以表示为n元组x={ x[1],…,x[n] }. x[i]∈{1,2,…,m},

解空间树为排序树,是一棵n+1层的完全m叉树.

在解空间树中做深度优先搜索, 约束条件:如果a[j][i]=1 , x[i] ≠ x[j]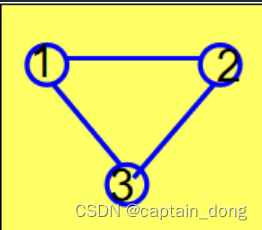
                                       

 m=3,n=3时的解空间树

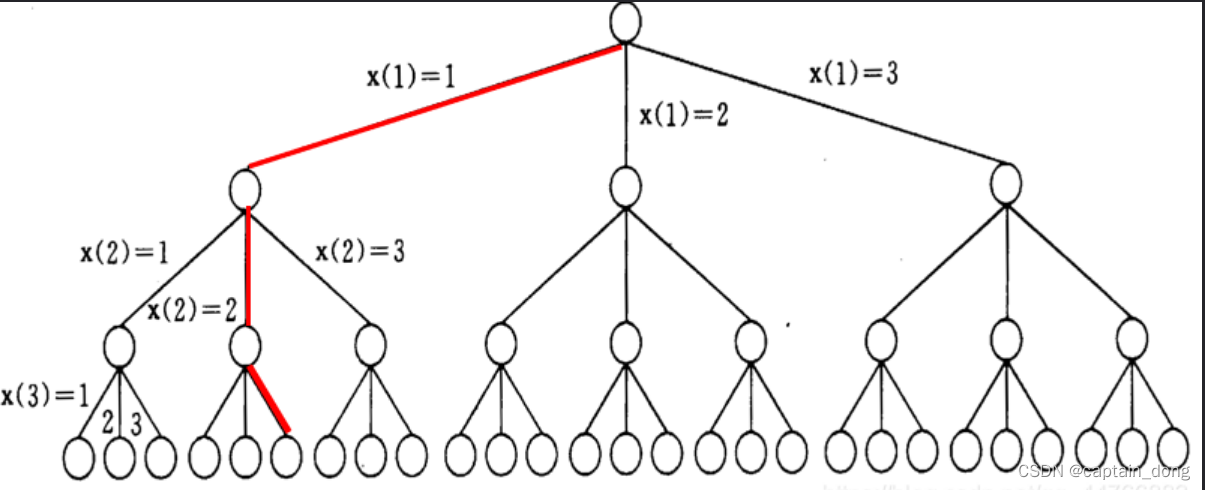
再举个例子

对于下图，写出图着色算法得出一种着色方案的过程。

顶点数量n=4, 色数：m=3

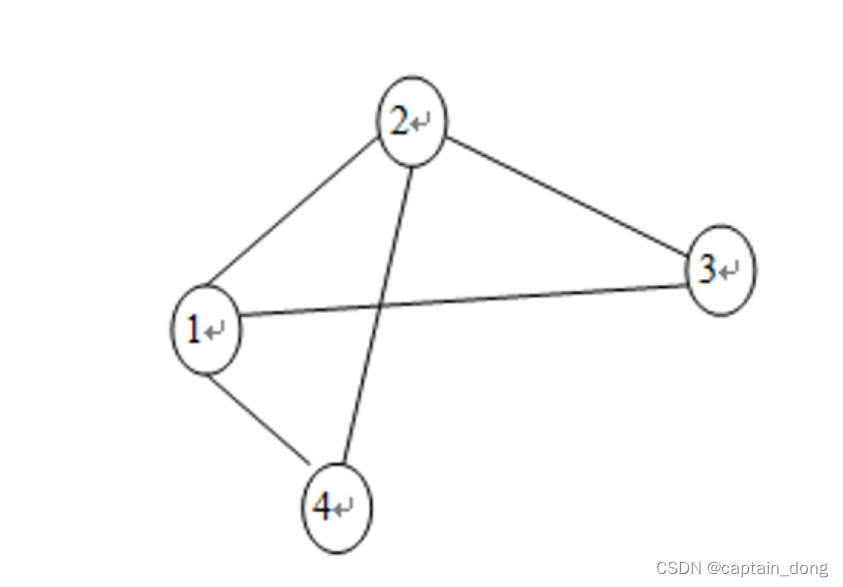
 m=4,n=3时的解空间树

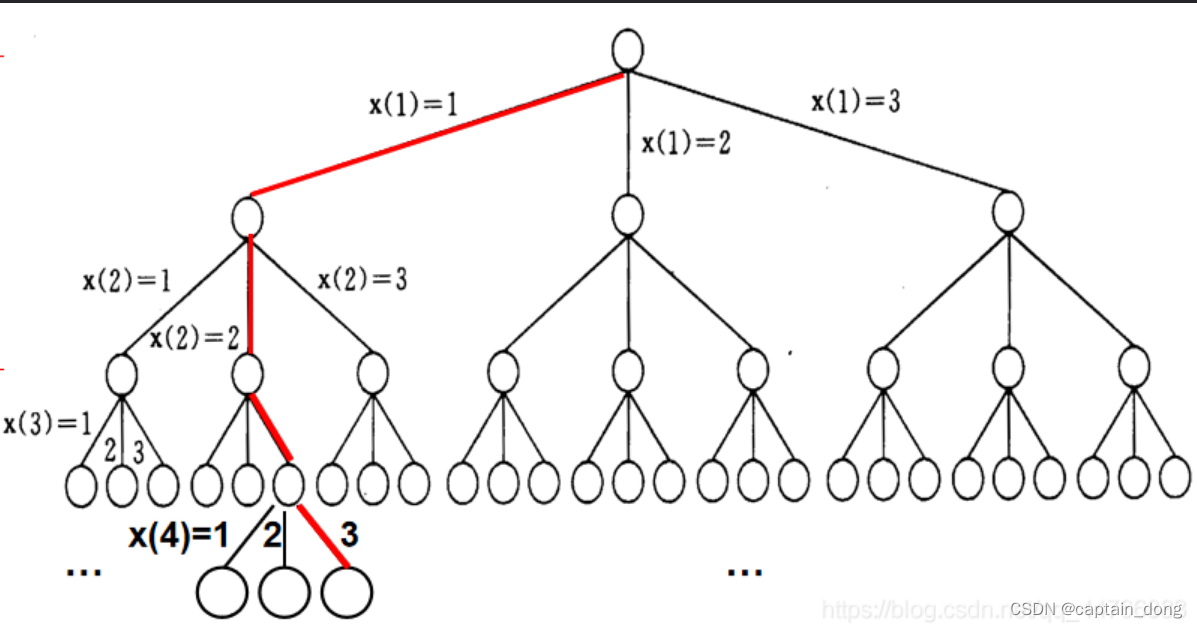
X[1]←1 , 返回 true
X[2]←1, 返回false; X[2]←2, 返回 true
X[3]←1 ,返回false; X[3]←2, 返回false;X[3]←3, 返回 true
X[4]←1, 返回false; X[4]←2, 返回false;X[4]←3, 返回 true

着色方案：（1，2，3，3）

复杂度分析

图m可着色问题的解空间树中，内结点个数是：

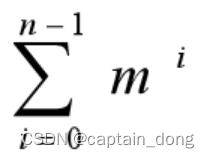
对于每一个内结点，在最坏情况下，用ok检查当前扩展结点每一个儿子的颜色可用性需耗时O(mn)。

因此，回溯法总的时间耗费是

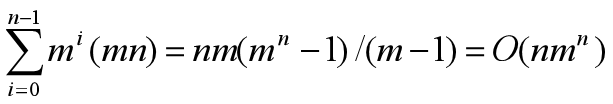
#include"图的着色.h"


const int NUM = 100;
int n;//顶点数
int m;//颜色数
int a[NUM][NUM];//图的邻接矩阵
int x[NUM];//当前的解向量
int sum = 0;//解的数量

bool same(int t) {
    int i;
    for (i = 1; i < n; i++) {//修正同色判断函数的循环范围
        if ((a[t][i] == 1) && (x[i] == x[t]))
            return false;
    }
    return true;
}

void BackTrack(int t) {
    int i;
    if (t > n) {
        sum++;
        cout << "解" << sum << ":" << endl;//输出当前解的编号
        for (i = 1; i <= n; i++) {
            cout << x[i] << " ";//按照节点顺序输出颜色
        }
        cout << endl;
    }
    else
    {
        for (i = 1; i <= m; i++) {
            x[t] = i;
            if (same(t))
                BackTrack(t + 1);
            x[t] = 0;
        }
    }
}

int main() {
    cin >> n >> m;
    //初始化邻接矩阵为0
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            a[i][j] = 0;
        }
    }
    //读入边，构建邻接矩阵
    int u, v;
    while (cin >> u >> v) {
        if (u < 1 || u > n || v < 1 || v > n) {//判断输入是否合法
            cout << "输入不合法！" << endl;
            continue;
        }
        a[u - 1][v - 1] = 1;
        a[v - 1][u - 1] = 1;
    }

    BackTrack(1);//从第1个节点开始

    cout << "一共有" << sum << "个解。" << endl;//输出解的数量

    return 0;
}