目录
1.Apriori算法
Apriori性质
伪代码
apriori算法
apriori-gen(Lk-1)【候选集产生】
has_infrequent_subset(c,Lx-1)【判断候选集元素】
例题
求频繁项集:
对于频繁项集L={B,C,E},可以得到哪些关联规则:
2.FP-growth算法
FP-tree构造算法【自顶向下建树】
insert_tree([plP],T)
利用FP-tree挖掘频繁项集
关联规则挖掘是数据挖掘领域中研究最为广泛的也最为活跃的方法之一
关联规则反应了一个事物和其他事物之间的相互依存性和关联性
如果存在一定的关联关系,其中一个事物就可以通过其他事物预测到
最小支持度:就是说当支持度达到一定的阈值后,某种数据才有被挖掘的潜力这个阈值就是最小支持度计数(min_sup)。
频繁项集:当某种数据的支持度超过最小支持计数阈值时就叫做频繁项集。
1.Apriori算法
Apriori算法是R.Agrawal和R.Srikant于1994年提出的为布尔关联规则挖掘频繁项集的原创性算法。
主要有以下几个步骤:首先通过扫描数据库积累每个项的计数,并收集满足最小支持度的项,找出频繁1-项集的集合(该集合记做L1)。然后L1用于找到频繁2-项集的集合L2,利用L2再找到L3,如此下去直到不能再找到频繁k-项集为止。
Apriori性质
频繁项集的所有非空子集也必须是频繁的。
非频繁项集的所有超集也必须是频繁的。
主要用于压缩拽索空间,从而更快地找到频繁项集。
伪代码
摘自《数据挖掘:方法与应用》徐华著
apriori算法
输人:数据集D;最小支持度计数minsup_count。
输出:频繁项目集L。//所有支持度不小于minsupport的1-项集
L1={频繁1-项集};
Ck=apriori-gen (L-1);//C是k个元素的候选集
for(k=2;Lk-1≠0;k++)
for all transaction t属于D
Ct=subset(Ck,t);
for all candidates c属于Ct
c.count++;
End for
End for
Lk={c∈Ck|c.count>=minsup_count}
End for
L=ULkapriori-gen(Lk-1)【候选集产生】
输入:(k-1)-项集
输出:k-候选集C。
for all itemset p∈Lk-1
for all itemset q∈Lk-1
if (p.item1=q.item1, p.item2=q.item2,…,p.itemk-2=q.itemk-2,p.itemk-1<q.itemk-1)
c=p∞q;
if(has_infrequent_subset(c,Lx-1)) delete c;
else add c to Ck;
End for
End for
Return Ckhas_infrequent_subset(c,Lx-1)【判断候选集元素】
输入:一个k-项集c,(k-1)-项集Lk-1
输出:c是否从候选集中删除。
for all (k-l)-subsets of c
if S不属于Lk-1
return true;
return false例题
假设最小支持度是2

求频繁项集:
- 频繁1-项集L1{A},{B},{C},{E};
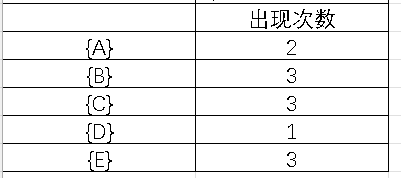
- 频繁2-项集L2:{A,C},{B,C},{B,E},{C,E};
- 频繁3-项集L3:{B,C,E};
说白了就是找哪种组合出现的次数>=2。
对于频繁项集L={B,C,E},可以得到哪些关联规则:
- B->C,Econfidence=2/2=100%
- C->B,Econfidence=2/3=67%
- E->B,Cconfidence=2/2=100%
- C,E->Bconfidence=2/3=67%
- B,E->Cconfidence=2/3=67%
- B,C->Econfidence=2/3=67%
2.FP-growth算法
FP-growth算法主要采用如下的分治策略:首先将提供频繁项的数据库压缩到一个频繁模式树(FP-tree),但仍保留相关信息。然后将压缩后的数据库划分成一组条件数据库,每个关联一个频繁项或“模式段”,并分别挖掘每个条件数据库。
FP-tree构造算法【自顶向下建树】
输人:事务数据库DB;最小支持度阈值Minsupport。
输出:FP-tree树。
(1)扫描事务数据库D一次。收集频繁项集合E以及它们的支持度计数,对F按照支持度计数降序排序,得到频繁项列表L。
(2)创建FP-tree的根节点,以“null"标记它。对于D中的每个事务T,作如下处理:选择T中的频繁项,并按照L中的次序进行排序,排序后的频繁项标记为[plP],其中p是第一个元素,P是剩余元素的表。调用insert_tree([plP],T)将此元组对应的信息加入到T中。
insert_tree([plP],T)
构造FP-tree算法的核心是insert_tree过程。Insert_tree过程是对数据库的一个候选项目集的处理,它对排序后的一个项目集的所有项目进行递归式的处理直到项目表为空。
(1)if(T有一个子女N使得N.item-name=p.item-name)
(2)N的计数加一
(3) else
(4)创建一个新节点N,将其计数设为1,链接到它的父节点T,并通过节点链结构将其链接到具有相同项名的节点。
(5)如果P非空,递归地调用insert_tree(P,N)。
利用FP-tree挖掘频繁项集
输入:构造好的FP-tree,事务数据库D,最小支持度阈值Minsupport。
输出:频繁项集。FP-growth(Tree,α)
(1)if(Tree含单个路径P)
(2)for路径P中节点的每个组合(记作β)
(3)产生模式βUα,其支持度support=β中节点的最小支持度
(4)else for each ai 在Tree的头部{
(5)产生一个模式β=aiUα,其支持度support=ai.support;
(6)构造β的条件模式基,然后构造β的条件FP-树Treeß;
(7) if Treeβ≠0 then
(8)调用FP_growth(Treeβ,β);
参考资料《数据挖掘:方法与应用》徐华著