本章思维导图:
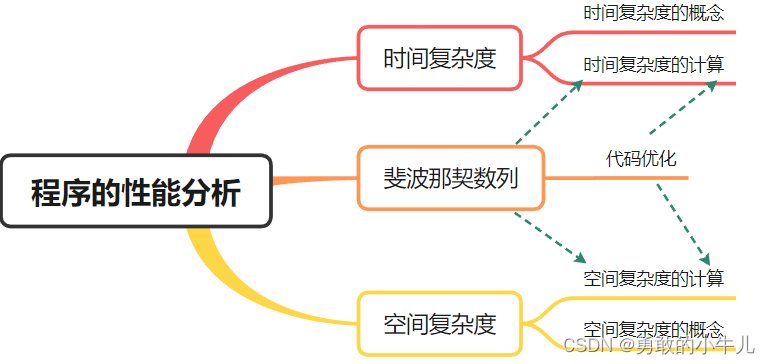
一,时间复杂度
1.1时间复杂度的概念
🌐:什么是时间复杂度呢?时间复杂度其实就是一个程序运行时它的指令运行的次数。
在这里,程序默认每条指令的运行时间是一样的。所以时间复杂度就可以理解为是程序内指令的运行次数。
说一千道一万,不如来个例子:
🌰:时间复杂度为O(n)
int main() {
int i = 0;
int n = 0;
scanf("%d", &n);
for (i = 0;i < n;i++) {
printf("执行%d次\n", i+1);
}
return 0;
}这个程序的时间复杂度便是O(n),这个程序的时间复杂度的计算其实就看for循环的执行次数,很明显for循环会执行n次,所以这个程序的时间复杂度是O(n)。
🌰:时间复杂度为O(n^2)
int main() {
int i = 0;
int j = 0;
int n = 0;
scanf("%d", &n);
for (i = 1;i <= n;i++) {
for (j = 1;j <= n;j++) {
printf("执行了%d次\n", i * j);
}
}
return 0;
}这个程序的时间复杂度便是O(n^2),因为这个程序有两个for循环。当第一层循环计算一次时,第二层循环就要计算n次。所以当第二层循环计算了n次时整个程序就计算了n^2次。所以这个程序的时间复杂度是O(n^2)。
1.2时间复杂度的计算
🌐:细心的小伙伴一定会发现我在对时间复杂度进行描述的时候使用了O()的表示方法。这个表示方法其实就叫作大O表示法。在算法导论里面,大O表示法表示的就是算法在最坏的情况下的运行时间。
1.2.1:大O表示法的几个计算特点
1.只保留最高阶的项
🌐因为计算机的运算速度十分的快,所以在一个程序内可能只有最高阶的项可以影响它。所以在我们使用大O表示法的时候,就可以舍弃其它项只保留最高阶的项来对程序的运行速度进行表示。在这里也表明了大O表示法注定是一个估计的值而不是一个精确的值。
举个例子:🌰
int main() {
int i = 0;
int j = 0;
int n = 0;
scanf("%d", &n);
for (i = 1;i <= n;i++) {
printf("执行了%d次\n", i);
}
for (i = 1;i <= n;i++) {
for (j = 1;j <= n;j++) {
printf("执行了%d次\n", i * j);
}
}
return 0;
}在这里,很明显我写的这个程序的执行次数是n+n^2次。但是当我们用大O表示法的时候,我们是不会用O(n+n^2)来表示。我们用的还是用O(n^2)来表示。因为在使用大O表示法时我们只保留最高阶的项。在这里就是n^2。
2.常数次用O(1)表示
🌐在程序中,如果指令只使用了常数次的话,那我们就可以用O(1)来表示这个程序的时间复杂度。不管这个常数有多大它的时间复杂度都是O(1),这是因为计算机的运行速度实在是太快了。
举个例子:🌰
int main() {
int i = 0;
for (i = 0;i < 5;i++) {
printf("执行%d次\n", i);
}
return 0;
}这个5是常数,所以这个for循环执行的次数是常数次。因此,这个代码的时间复杂度就是O(1)
int main() {
int i = 0;
for (i = 0;i < 50000000;i++) {
printf("执行%d次\n", i);
}
return 0;
}现在把5换成50000000,即使大小变大了很多。但是50000000还是一个常数,所以这个代码的时间复杂度还是O(1)。
3.大O表示法里的logn的底数是2 而不是10
🌐我们大多数的初学者可能已经习惯了logn的底数是10了,但是要时刻记住在计算机中logn的底数是2。
二,空间复杂度
2.1空间复杂度的概念
🌐什么是空间复杂度呢?空间复杂度就是一个算法在运行过程中占用内存空间的大小的度量。这个内存空间与执行文件的大小没有半毛钱的关系。也就是说时间复杂度与执行文件的大小没有关系。
举个例子:
🌰
int main() {
int i = 0;
int n = 0;
scanf("%d", &n);
for (i = 0;i < n;i++) {
printf("执行%d次\n", i+1);
}
return 0;
}这个程序的空间复杂度便是O(1),因为这个程序创建的变量是可数的,只有2个。所以它的空间复杂度就是O(1)
int main() {
int i = 0;
int n = 0;
scanf("%d", &n);
int arr[] = { 0 };
for (i = 0;i < n;i++) {
arr[i] = i;
}
return 0;
}像这个代码的空间复杂度便是O(n)因为这个代码要开辟n个空间大小的数组,所以这个程序的空间复杂度就是O(n)。
2.2空间复杂度的计算
空间复杂度的计算其实时间复杂度的计算差不多,只是计算的对象从时间变成了空间。
只要套用时间复杂度的计算方法,然后再将计算时间变成计算空间就可以了。
3.斐波那契数列的时间与空间复杂度的计算方法
3.1斐波那契数列的介绍
斐波那契数列又名兔子数列,像:1,1,2,3,5,8,13,21,34,55,89
这样的数列就是一个斐波那契数列。可以很明显的看出斐波那契数列的特点是从第三项开始,每一项都等于前两项的和。
现在我们来编写一个代码来求斐波那契数列的第n项的结果:
代码如下:
int Fib(int n) {
if (n <= 0) {
return 0;
}
else if (n == 1) {
return 1;
}
else {
return Fib(n - 1)+Fib(n-2);
}
}
int main() {
int n = 0;
scanf("%d", &n);
int ret = Fib(n);
printf("%d\n", ret);
return 0;
}这段代码确实容易写出来,但现在的问题是:这段代码的时间复杂度是多少呢?空间复杂度是多少呢?
3.1时间复杂度
要算时间复杂度,其实就是要算这个递归调用了多少次Fib()函数。那我们只要求出这段代码调用了多少次Fib函数便大功告成了。
3.2 计算时间复杂度
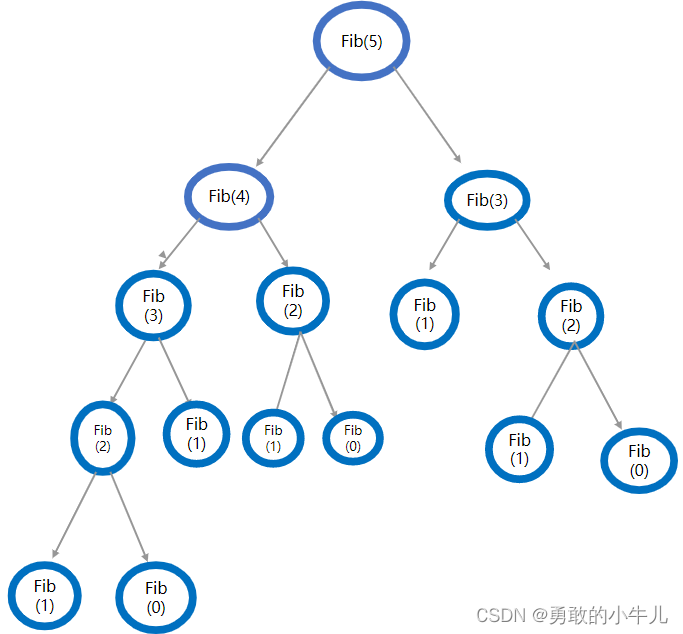
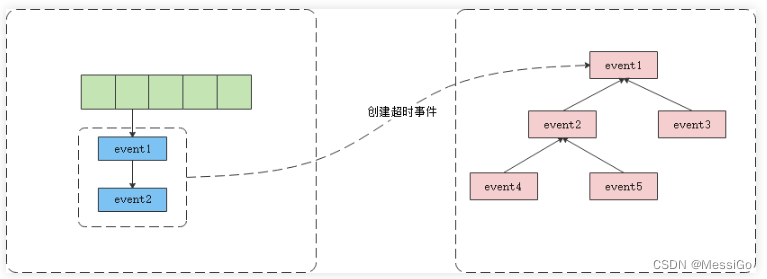
现在假设n==5,计算一下时间复杂度。计算这个时间复杂度便是要计算函数Fib被调用的次数,现在我借助图像来详细介绍一下Fib函数被调用的次数:
在这个图里面,可以清楚的数出来这个图里面的节点数有15个。当我们用一个阶乘的方式来表示15时,15==2^(n-1)-1==(2^n)/2-1。当我们用大O 表示法来表示的时候就变成了O(2^n)。(只保留最高一层项)。
3.3空间复杂度
这个斐波那契数列的空间复杂度是什么呢?众说周知,空间复杂度表示的是在一个程序在运行时开辟的空间大小。在递归中这个空间该怎么算了?递归中的空间复杂度是:递归深度*每次递归时的空间复杂度。像上面的Fib(5)的空间复杂度就是O(1)*5。递归的空间复杂度就是O(5)。当我们将这个空间复杂度一般化时,它的空间复杂度就是O(n)。
3.4优化
可以看到这个递归的时间复杂度是非常大的,当n非常大的时候这种递归的方法的耗时就会非常长。所以我们要对这个递归方法进行优化来让它变得高效一点。在这里优化的目的就是减少递归的次数,也就是将return Fib(n-1)+Fib(n-2)改一下。
优化:时间复杂度
int Fib(int first, int second, int n) {
if (n <= 0) {
return 0;
}
else if (n < 3) {
return 1;
}
else if (n == 3) {
return first + second;
}
else {
return Fib(second, first + second, n - 1);//将两次递归改为一次
}
}
int main() {
int n = 0;
scanf("%d", &n);
int ret = Fib(1,1,n);
printf("%d\n", ret);
return 0;
}
这个程序的时间复杂度是多少呢?答案是O(n),空间复杂度也是O(n)。
再次优化:优化空间复杂度
int main() {
int a = 1;
int b = 1;
int c = 1;
int n = 0;
scanf("%d", &n);
n = n - 2;
while (n--) {
c = a + b;
a = b;
b = c;
}
printf("%d\n", c);
return 0;
}这个程序的空间复杂度就是O(1),时间复杂度还是O(n).
结束,今天的分享就到此为止,谢谢你的阅读。