前言：栈和队列是常用的数据结构之一，本文主要介绍有关栈的基本特性以及基本操作和一些经典的OJ题目，关于队列的介绍放到下篇。那么话不多说，让我们开始吧。

一、栈的基本知识

1. 栈的基本概念

栈是一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。栈中的数据元素遵守后进先出 LIFO（Last In First Out） 的原则。
下面是简单的示意图，请看：
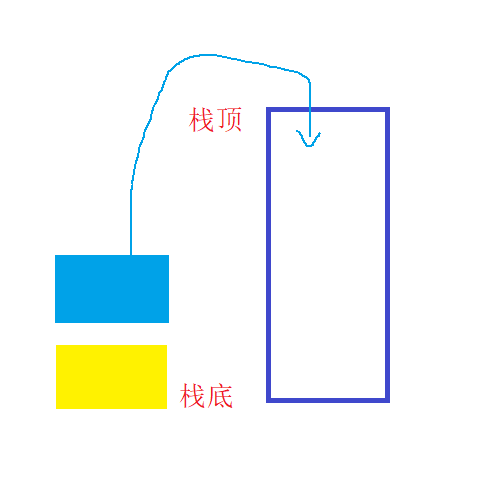
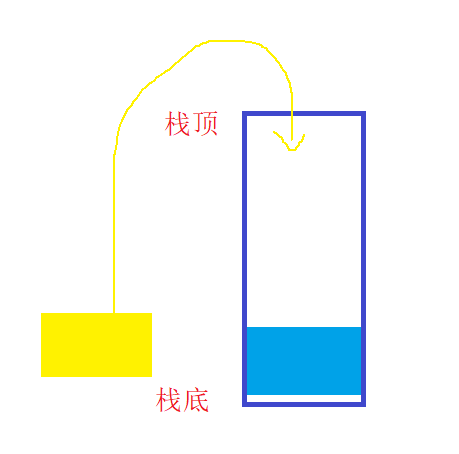
入栈时，蓝色方块先入栈后，黄色方块再入栈


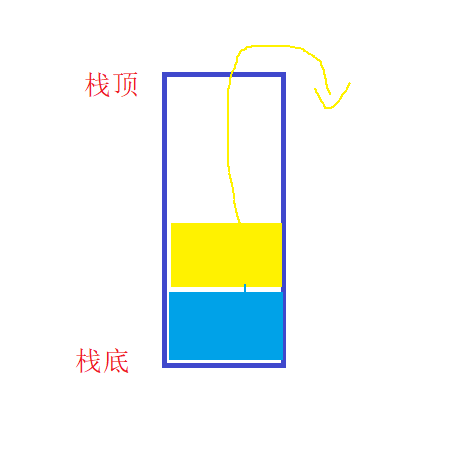
出栈时，黄色方块先出栈，蓝色方块再出栈：

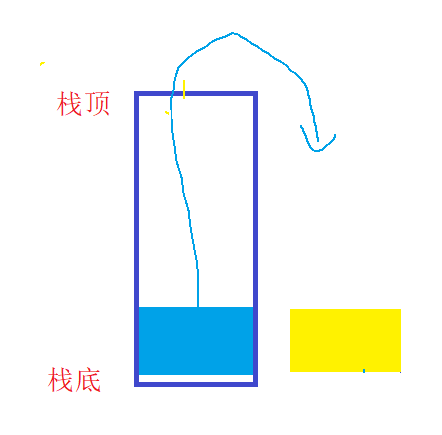
2. 栈的存储方式

由概念可知，栈是一种特殊的线性表，故存储方式自然也就分为两种，顺序存储（顺序栈）和链式存储（链栈）。关于具体实现细节与其常用的存储方式会在下一部分进行说明。

二、栈的结构定义

1. 顺序栈

即通过顺序表，也就是数组的形式实现栈，其结构体定义如下：

typedef struct Stack
{
	STDataType* a;	//动态栈，空间不够则进行分配
	int top;		//栈顶指针
	int capacity;	//栈的容量
}Stack;

2. 链栈

即通过链表的形式实现栈，其结构体定义如下：

//单链表节点的结构定义
typedef struct SListNode
{
	SLTDateType data;
	struct SListNode* next;
}SListNode;

//链栈的结构定义
typedef struct Stack
{
	SListNode* top;		//栈顶指针
	int capacity;	//栈的容量
}Stack;

关于链栈还有一点需要注意的是：由于栈先进后出的特性，需要将单链表的第一个节点作为栈顶指针

说明一下：关于栈的存储方式我们一般使用的是顺序存储结构，因为其相比于链式存储结构来说，操作简单，便于实现，而且很关键的一个原因就在于栈的特性是 “先进后出”，即只能在栈顶一端进行删除，这就很好利用了顺序表尾删的便捷，又规避了顺序表除尾删外其他位置删除需要挪动元素的不便。

文章接下来关于栈的介绍也建立在顺序栈的基础上。

三、栈的基本操作

前言：在进行基本操作的介绍之前，这里先对栈顶指针的具体指向进行一个说明。一般来说，栈顶指针可以指向栈顶元素，也可以指向栈顶元素的下一个位置；前者需要将栈顶指针初始化为-1，后者需要将栈顶指针初始化为0。
参考示意图如下：

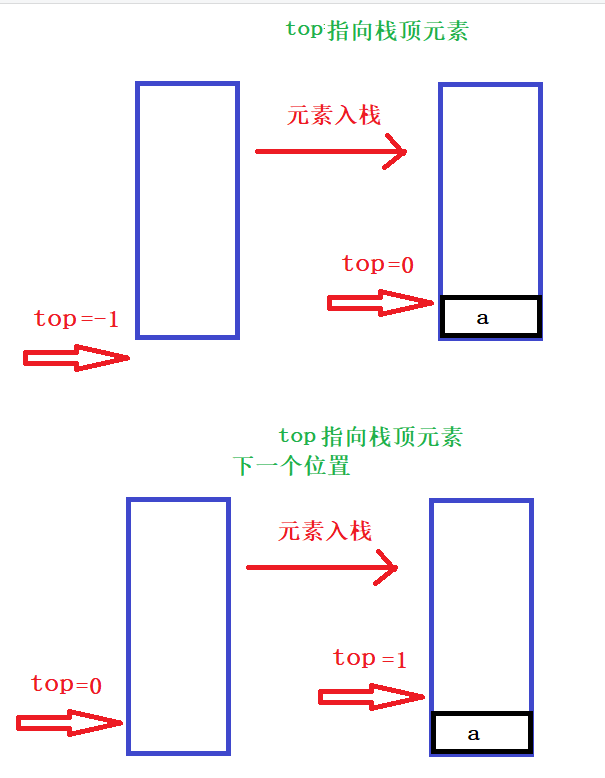
本文对栈的介绍采用的是栈顶指针指向栈顶元素的下一个位置的模式。

1. 栈的初始化

通过初始化操作为栈开辟空间，并将相应结构成员信息进行初值设置。
（1）操作执行的过程

• 为栈动态开辟一块内存空间，开辟空间的大小可通过define定义常量进行设定；
• 将栈的容量初始化为设定的常量值；
• 将栈顶指针初始化为0；

（2）具体代码：

void StackInit(Stack* ps)
{
	assert(ps);
	
	//开辟空间
	STDataType* tmp = (STDataType*)malloc(sizeof(STDataType) * DEF_CAP);
	if (tmp == NULL)
	{
		perror("malloc failed");
		return;
	}
	ps->a = tmp;
	//初始化
	ps->capacity = DEF_CAP;
	ps->top = 0;		//top指向栈顶元素的下一个元素
}

（注：代码中的DEF_CAP是由define定义的常量，表示默认的容量值）

2. 栈的销毁

有建立肯定需要配套一个销毁；在栈用完时需要对其进行销毁（将空间还给操作系统）
（1）操作执行的过程：

• 将在初始化操作中所开辟的空间进行释放；
• 将相应结构成员信息进行置零；

（2）具体代码：

void StackDestroy(Stack* ps)
{
	assert(ps);

	//释放开辟的空间，并置空
	free(ps->a);
	ps->a = NULL;
	//相应结构成员信息置零
	ps->capacity = 0;
	ps->top = 0;
}

3. 判断栈是否为空

（1）操作的执行过程：

• 对栈顶指针进行判断即可，由于采用的是栈顶指针指向的栈顶元素下一个位置的模式，故判断栈顶指针是否等于0即可

（2）具体代码：

bool IsStackEmpty(Stack* ps)
{
	assert(ps);

	return (ps->top == 0);
}

4. 入栈

（1）操作的执行过程：

• 通过栈顶指针判断栈空间是否已满，若已满，则需进行扩容，扩容的大小也可通过define定义常量进行设定；扩容完毕后，注意更新栈的容量信息；
• 将值存放到栈顶指针指向位置所对应的空间后，栈顶指针再进行++操作；

（2）具体代码：

void StackPush(Stack* ps, STDataType x)
{
	assert(ps);

	//检查栈是否已满
	if (ps->top == ps->capacity)
	{
		STDataType*tmp = (STDataType*)realloc(ps->a,  sizeof(STDataType)*(ps->capacity+INC_CAP));
		if (tmp == NULL)
		{
			perror("realloc failed");
			return;
		}
		ps->a = tmp;
		//注意更新栈的容量信息
		ps->capacity += INC_CAP;
	}
	//进行赋值后栈顶指针再++
	ps->a[ps->top++] = x;
}

（注：代码中的INC_CAP为define定义的常量，表示扩容量的值）

5. 出栈

（1）操作执行过程：

• 进行出栈前需先进行栈是否为空的判断，若为空则也通过assert断言进行报错
• 由于是通过顺序表（数组）来实现栈，故控制栈的访问权限就只取决于栈顶指针top的位置，即出栈并不是真正将栈顶的元素“ 删除” 或 “释放”掉，而直接让栈顶指针的--而不去访问那个空间即可。

（2）具体代码：

void StackPop(Stack* ps)
{
	assert(ps);
	assert(!IsStackEmpty(ps));

	ps->top--;
	//直接让栈顶指针--即可
}

6. 访问栈顶元素

（1）操作执行过程：

• 先判断栈是否为空，若为空则需通过assert断言报错；
• 通过栈顶指针将栈顶元素（数组中最后一个元素）的值返回即可。

（2）具体代码：

STDataType StackTop(Stack* ps)
{
	assert(ps);
	assert(!IsStackEmpty(ps));

	return ps->a[ps->top - 1];
	//栈顶指针指向栈顶元素的下一个位置
}

如上就是一些栈的基本操作啦，关于栈部分完整的头文件以及源文件大家如果有需要的话可以从博主的码云仓库中自行获取，这里是链接：DataStructure
掌握了这些基本操作后我们就可以尝试着去解决一些问题了，那么下面我们开始进入实战环节。

四、关于栈的OJ

1. 括号匹配问题

原题链接在这：
有效的括号
解题思路：
字符串中的左括号一定会和字符串中于其相隔最近的右括号进行匹配，结合栈先进后出的特点，我们可以每当遇到左括号时，就让该左括号入栈；每当遇到右括号时就让栈顶的左括号出栈来和该右括号进行匹配，若匹配成功则说明该括号有效，继续进行下一组匹配；若匹配失败，则直接返回；

由解题思路可将具体的操作过程归结为两步：

• 遍历字符串，每遇到左括号就让该左括号入栈；
• 每遇到右括号就让栈顶元素的左括号出栈，与其进行匹配；

有了具体的操作后，还有一些需要注意的特殊情况：

• 字符串中可能只有左括号或者左括号的数量多于右括号，此时不属于有效的匹配；由于遍历完字符串后括号都为有效匹配栈一定为空，故可在遍历完字符串后判断栈是否为空来解决这个问题；
• 字符串中可能只有右括号或者第一个字符就为右括号，此时不属于有效的匹配；由于匹配需要进行出栈操作，而此时的栈一定为空栈，故可通过判断栈是否为空来解决这个问题；

结合以上说明。我们就可得到具体代码如下：

//1.左括号就入栈
//2.右括号就出栈与其进行匹配
typedef struct Stack
{
	char* a;
	int top;
}Stack;

//初始化
void StackInit(Stack* ps)
{
	char* tmp = (char*)malloc(sizeof(char) * 10001);
	ps->a = tmp;
	ps->top = -1;		
}

//入栈
void StackPush(Stack* ps, char x)
{
	ps->a[++ps->top] = x;
}

//出栈
char StackPop(Stack* ps)
{
	return ps->a[ps->top--];
}

bool isValid(char * s)
{
    if(strlen(s) < 2)
        return false;

    Stack st;
    StackInit(&st);
    char* mov = s;
    while(*mov)
    {
        if((*mov == '(') || (*mov == '[') || (*mov == '{'))
        {
            StackPush(&st,*mov);
        }
        else
        {
            if(st.top == -1)    //第一个就是右括号
                return false;
            
            if(*mov == ')' && StackPop(&st) != '(')
                return false;
            if(*mov == ']' && StackPop(&st) != '[')
                return false;
            if(*mov == '}' && StackPop(&st) != '{')
                return false;         
        }
        mov++;
    }

    if(st.top != -1)    //有效字符串匹配完成后栈一定为空，即top为-1
        return false;
        
    return true;
}

（PS：解题代码中的出栈操作和在对栈的基本操作的介绍中的操作有一些区别：解题代码中的出栈操作相当于将访问栈顶元素和出栈结合起来了，即可理解为先获取了栈顶元素的信息，然后进行了出栈操作。）

本章完。

看完觉得有觉得帮助的话不妨点赞收藏鼓励一下，有疑问或有误地方的地方还恳请过路的朋友们留个评论，多多指点，谢谢朋友们！🌹🌹🌹