题目：剑指 Offer 53 - I. 在排序数组中查找数字 I - 力扣（Leetcode）

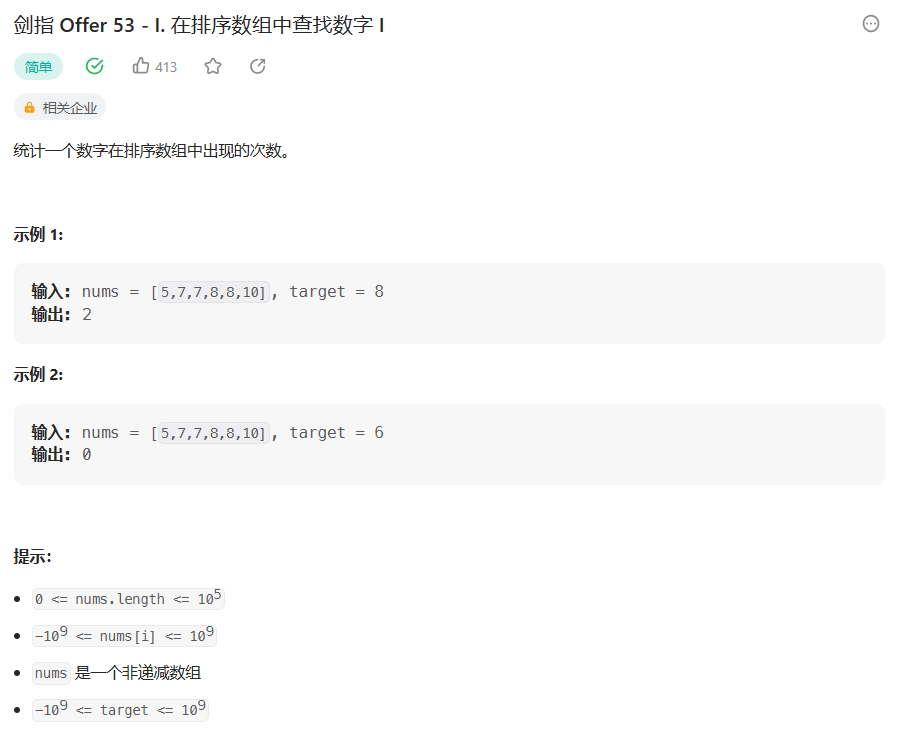
题目的接口：

class Solution {
public:
    int search(vector<int>& nums, int target) {

    }
};

解题思路：

那么这道题呢，

如果只是作为一道题，或者说笔试题，

我们当然是二话不说直接暴力拿下，

来看代码：

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int cnt = 0;
        for(auto e : nums) if(e == target) cnt++;
        return cnt;        
    }
};

是的，就是这么简单，三行代码暴力拿下，

但是，很显然，这道题肯定不只是让你随便暴力拿下，

如果是在面试的时候，面试官让你讲讲这道题，你确实可以先给面试官

讲讲暴力的解法，但要是你只会暴力，那估计就要直接回家等通知了，

很显然，作为一个有序数组，这道题可以用二分进行优化：

我们可以通过二分法确定左右边界，然后让右边界 - 左边界 + 1求出答案。

具体思路如下：

先确定右边界：（让左下标一直往右边靠）

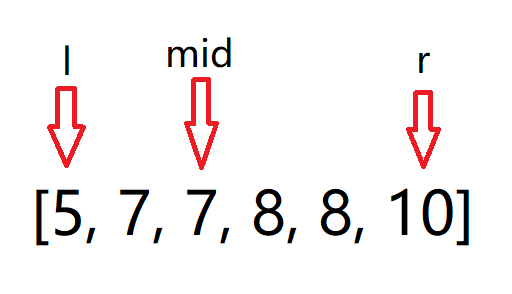
如果 nums[mid] <= target，就让 left = mid + 1;

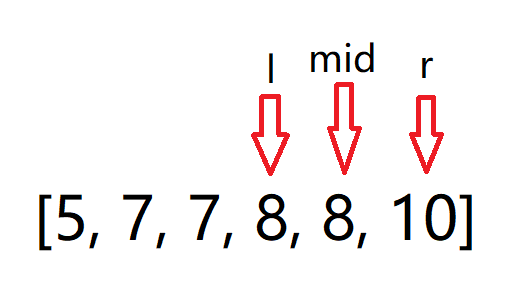
让左下标一直往右边走：

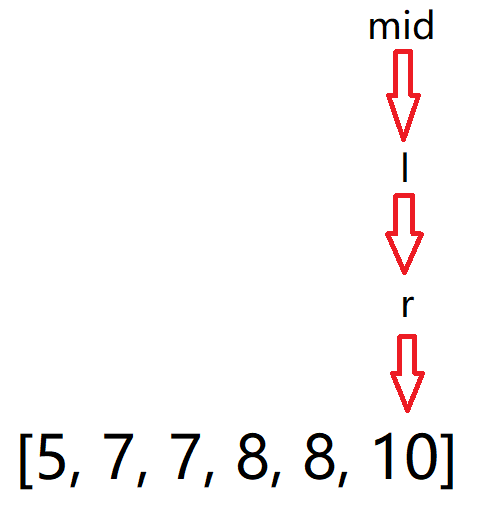
直到走出taget位置，让右下标往右靠：

这样 left > right ，循环结束，找到右边界left，

特殊情况：

1. 如果数组内不存在target，right所在位置就不是target；

2. 如果数组不存在target且数组内所以元素都 > target 或者数组根本没有元素，right就 < 0

也就是right会跑出数组，甚至本来就不在数组里面，

这两种情况就直接返回 0 表示不存在 target 值。

接下来是确定左边界，我们现将求出的右边界存下来：

（让右下标一直往左走）

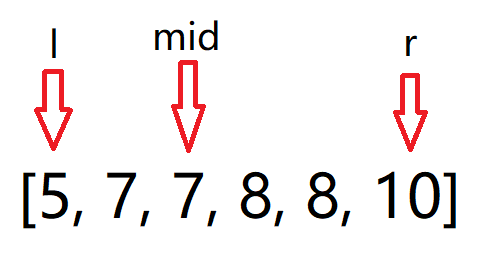
如果 nums[mid] < target，就让 left = mid + 1;

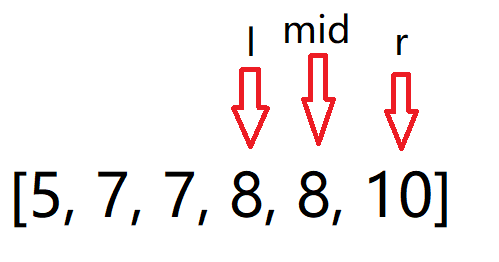
如果 nums[mid] >= target，就让 right = mid - 1;

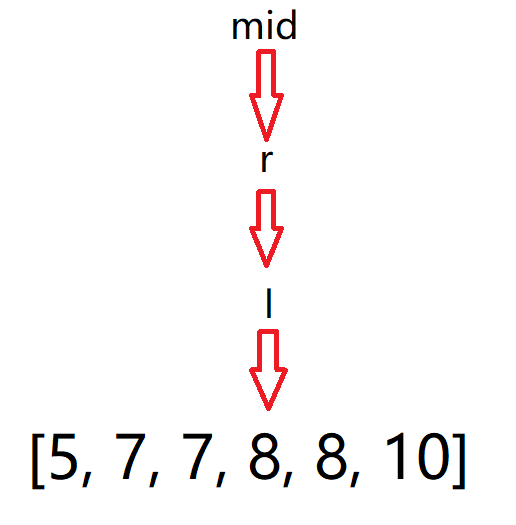
让右下标一直往左走：

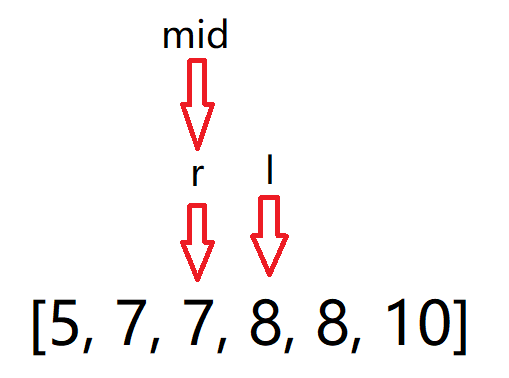
这样 left > right ，循环结束，找到左边界right，

最后再让右边界 - 左边界 + 1 即可，

下面是具体代码：

代码：

class Solution {
public:
    int search(vector<int>& nums, int target) {
        //先确定右边界
        int left = 0, right = nums.size() - 1;
        while(left <= right) {
            int mid = (left + right) >> 1;
            if(nums[mid] <= target) left = mid + 1;
            else right = mid - 1;
        }

        //右边界如果跑出数组或者所在位置不等于target，证明数组内没有target，就直接返回0
        if(right < 0 || nums[right] != target) return 0;

        //将右边界存下来
        int r = right;

        //再确定左边界
        left = 0, right = nums.size() - 1;
        while(left <= right) {
            int mid = (left + right) >>  1;
            if(nums[mid] < target) left = mid + 1;
            else right = mid - 1;
        }

        //返回：右边界 - 左边界 + 1
        return r - left + 1;
    }
};