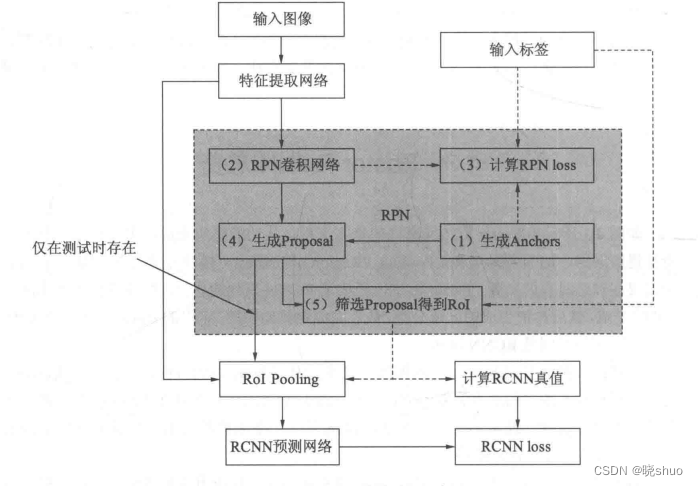
BCEWithLogitsLoss是一种用于二分类问题的损失函数，它将Sigmoid函数和二元交叉熵损失结合在一起。

假设我们有一个大小为$N$的二分类问题，其中每个样本$x_i$有一个二元标签$y_i\in 0,1$，并且我们希望预测每个样本的概率为$p_i\in [0,1]$。则BCEWithLogitsLoss可以表示为：

其中，$\sigma (x)=\frac{1}{1+e^{-x}}$是Sigmoid函数，$\log$是自然对数。在实践中，由于数值计算的稳定性问题，通常使用函数库中提供的BCEWithLogitsLoss函数来计算损失。

$p_i$表示样本$x_i$被预测为正例（1）的概率。在二分类问题中，BCEWithLogitsLoss通常用于处理模型输出的logits（即未经过Sigmoid函数激活的输出），通过将logits作为输入，结合Sigmoid函数进行概率估计和损失计算。在计算过程中，BCEWithLogitsLoss会首先对logits进行Sigmoid激活，然后计算预测概率和二元交叉熵损失。

$y_i$表示样本$x_i$的真实标签。在二分类问题中，$y_i$通常为0或1，表示样本$x_i$是否属于正例（1）类别。在BCEWithLogitsLoss中，$y_i$用于计算二元交叉熵损失，帮助模型学习将预测结果和真实标签匹配的能力。具体来说，当$y_i=1$时，BCEWithLogitsLoss会惩罚模型的预测值偏离1的程度；当$y_i=0$时，BCEWithLogitsLoss会惩罚模型的预测值偏离0的程度。因此，$y_i$在BCEWithLogitsLoss中是非常重要的一部分。