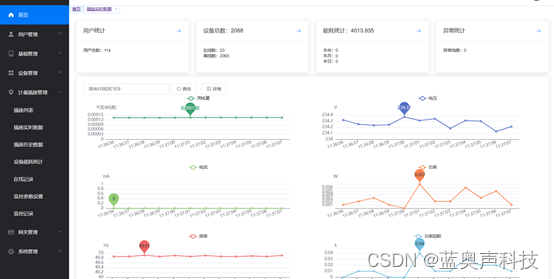
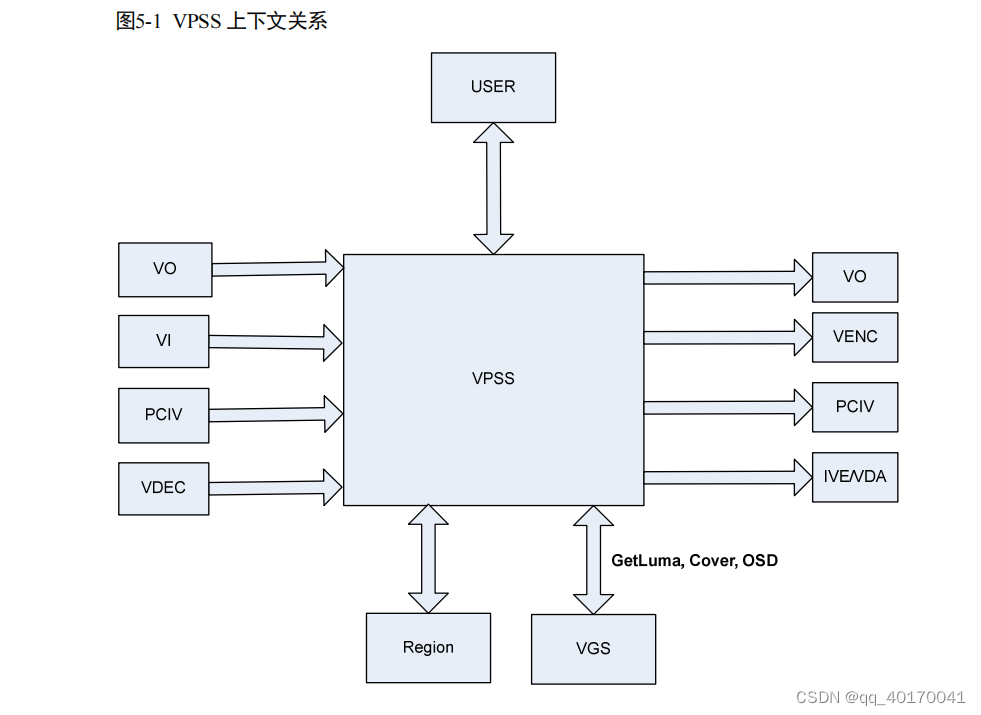
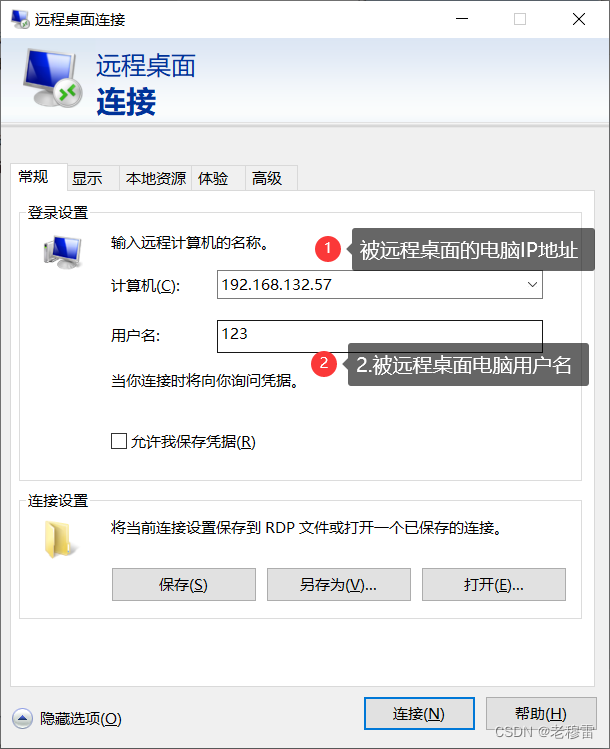
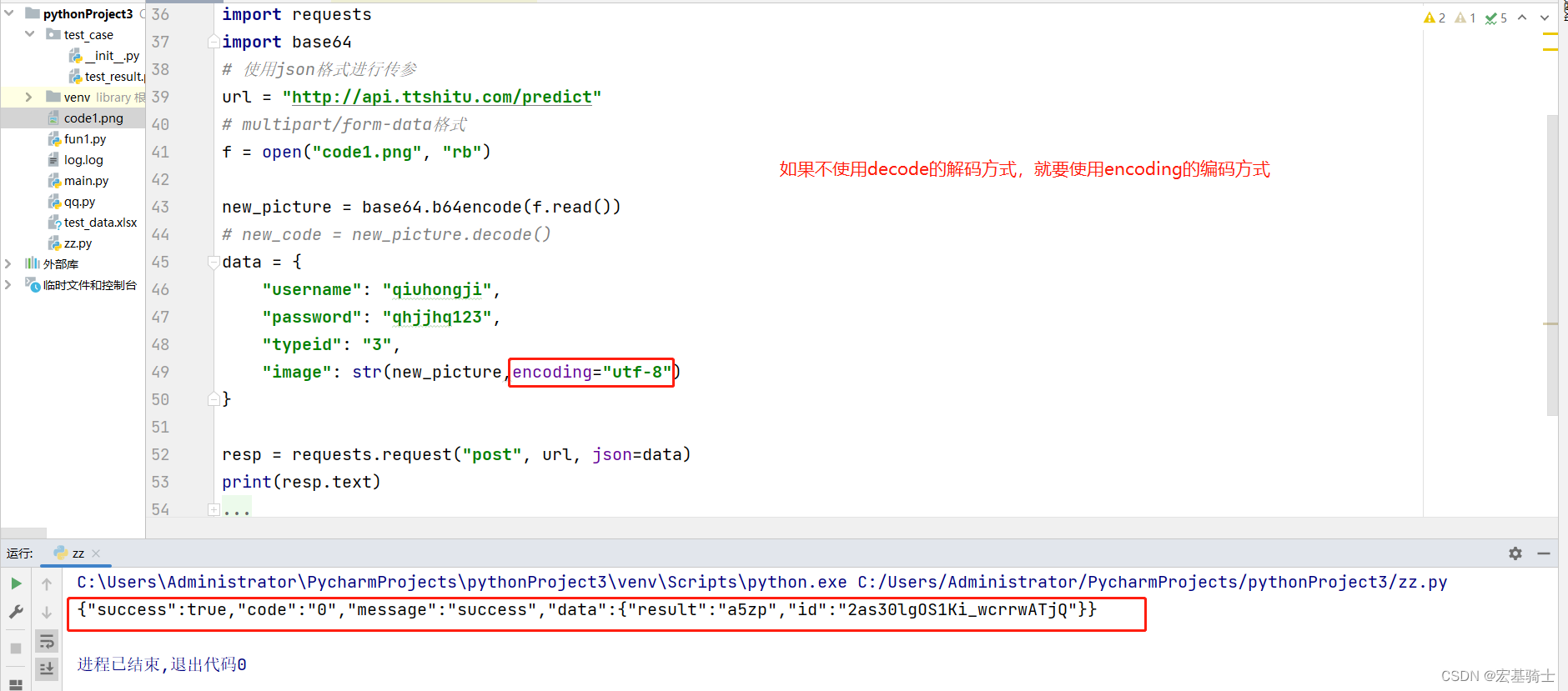
微分中值定理—柯西中值定理
前面我们已经学习了罗尔中值定理,和拉格朗日中值定理,它们的相同点是,研究的曲线都能用函数来表示。那假如曲线不能被函数表示呢,用柯西中值定理。
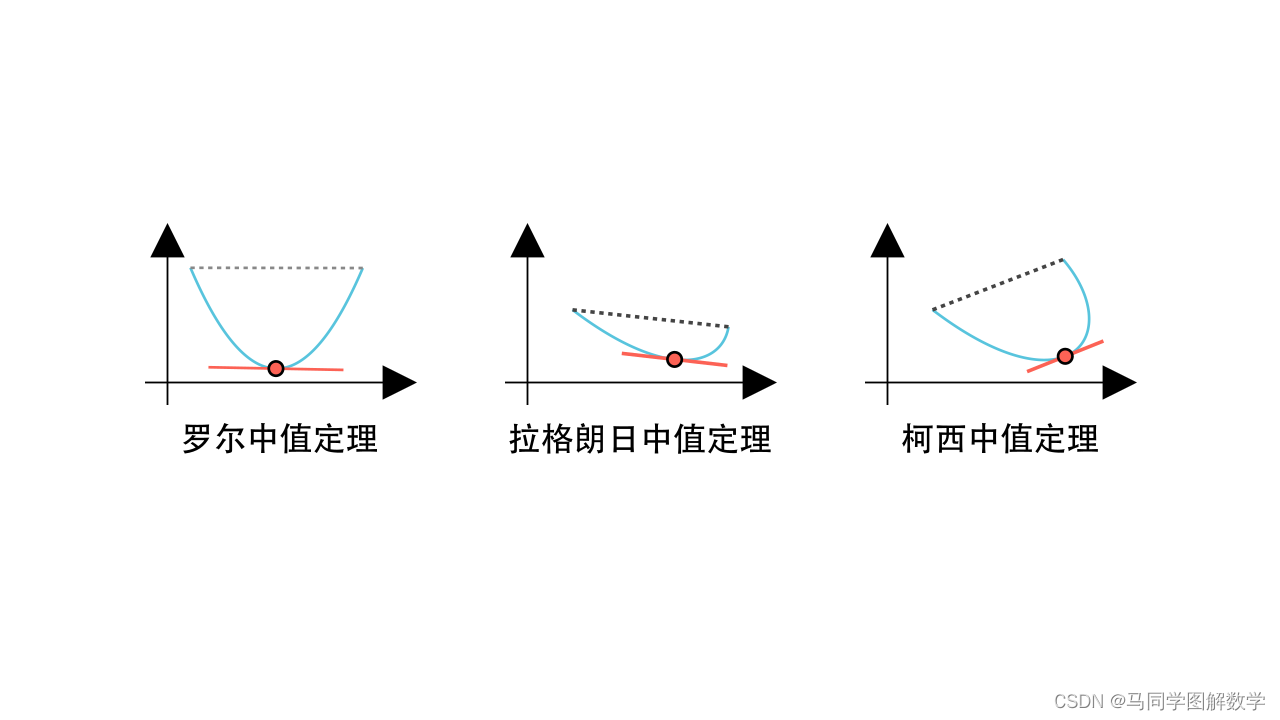
1 定义
柯西中值定理是拉格朗日中值定理的推广。如果,我们把研究对象扩展到两个函数,然后,将结论 ,再加上分母不为零的条件。那么拉格朗日中值定理,就成了我们的柯西中值定理如果函数
及
满足
那么 ,使得
。如果此时还有
,那么该式可改写为:
定义看完了,下面来看看它的几何意义
2 几何意义
要直观理解柯西中值定理,需要将 和
组成参数方程组。为了符合习惯,这里的自变量用
来表示,即假设有参数方程:
下面以 为横坐标,
为纵坐标,建立坐标系。起点为
时的位置
,终点为
时的位置
。
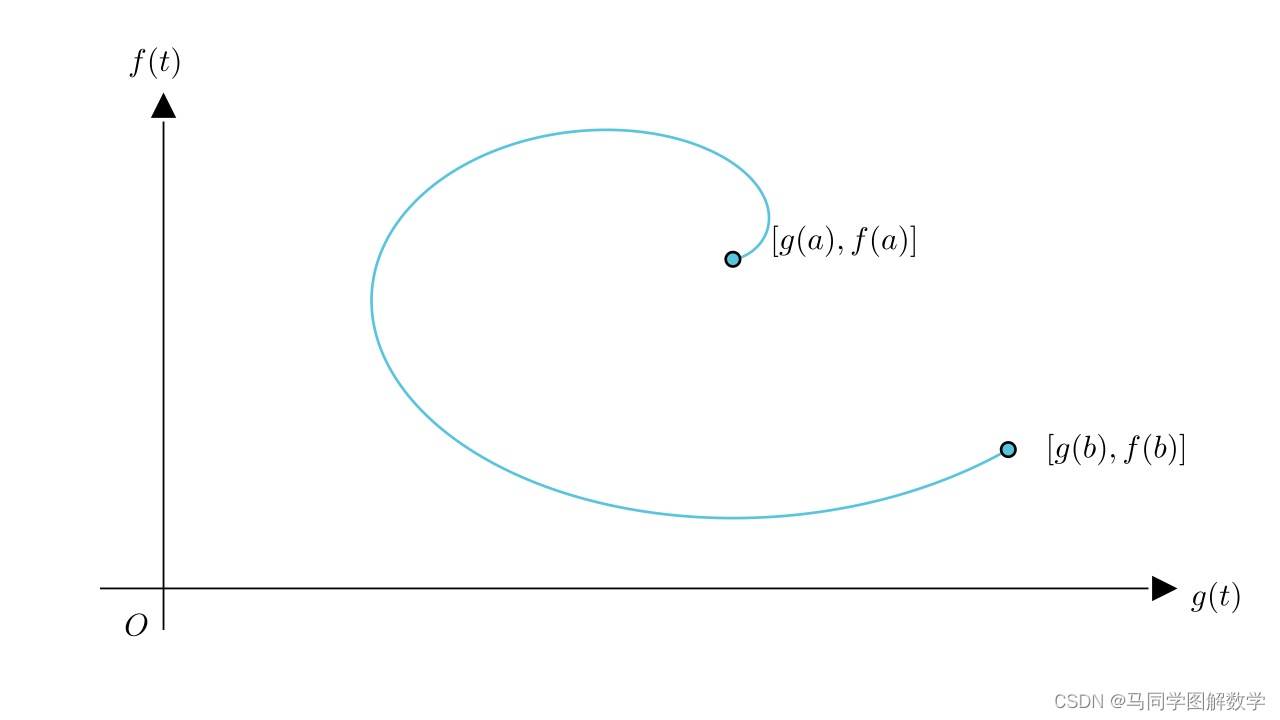
连接起点与终点,做出一条割线,那么 表示的就是割线的斜率。而
,表示的是,
这个位置,切线的斜率。
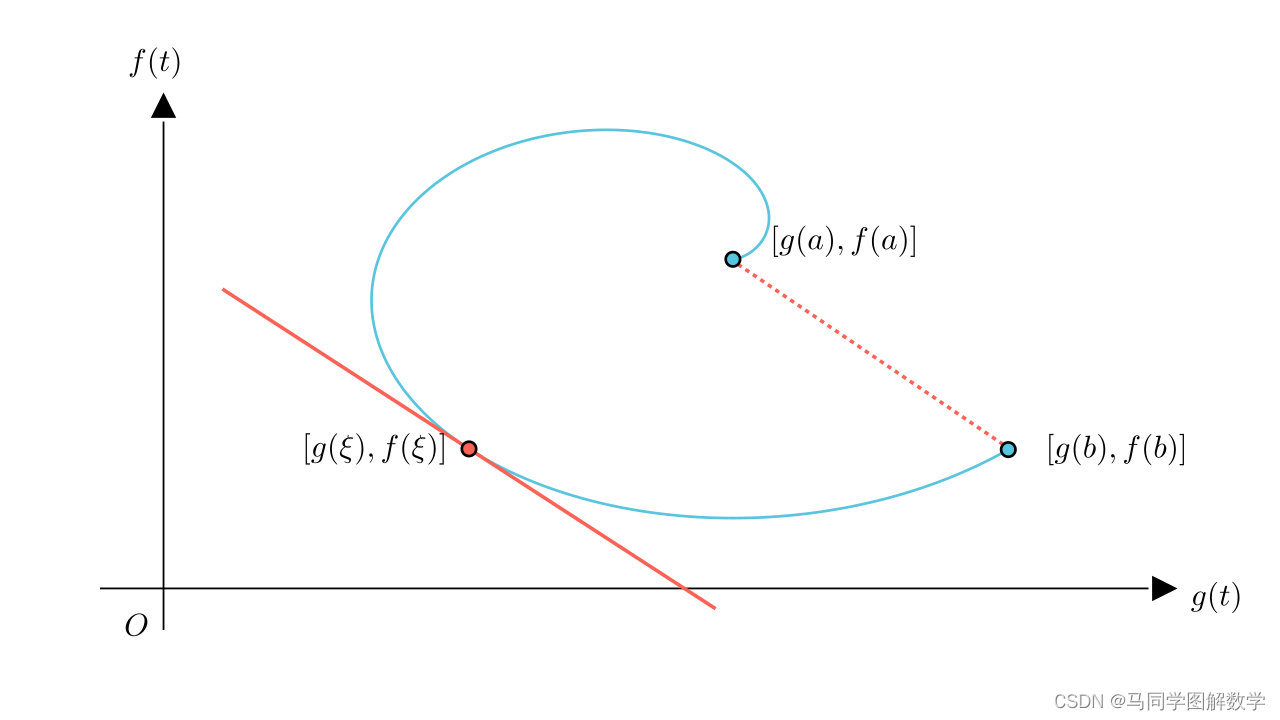
这样柯西中值定理的结论就是,曲线上至少有一点,它的切线的斜率与割线斜率是相等的。从几何上来讲,也就是 这个点的切线,与割线是平行的。
3 联系
前面说过,拉格朗日中值定理是罗尔中值定理的推广,这在几何上就可以体现。比如下面这条蓝色曲线,因为它能用函数表示,且闭曲间连续,开区间可导。所以符合拉格朗日中值定理。
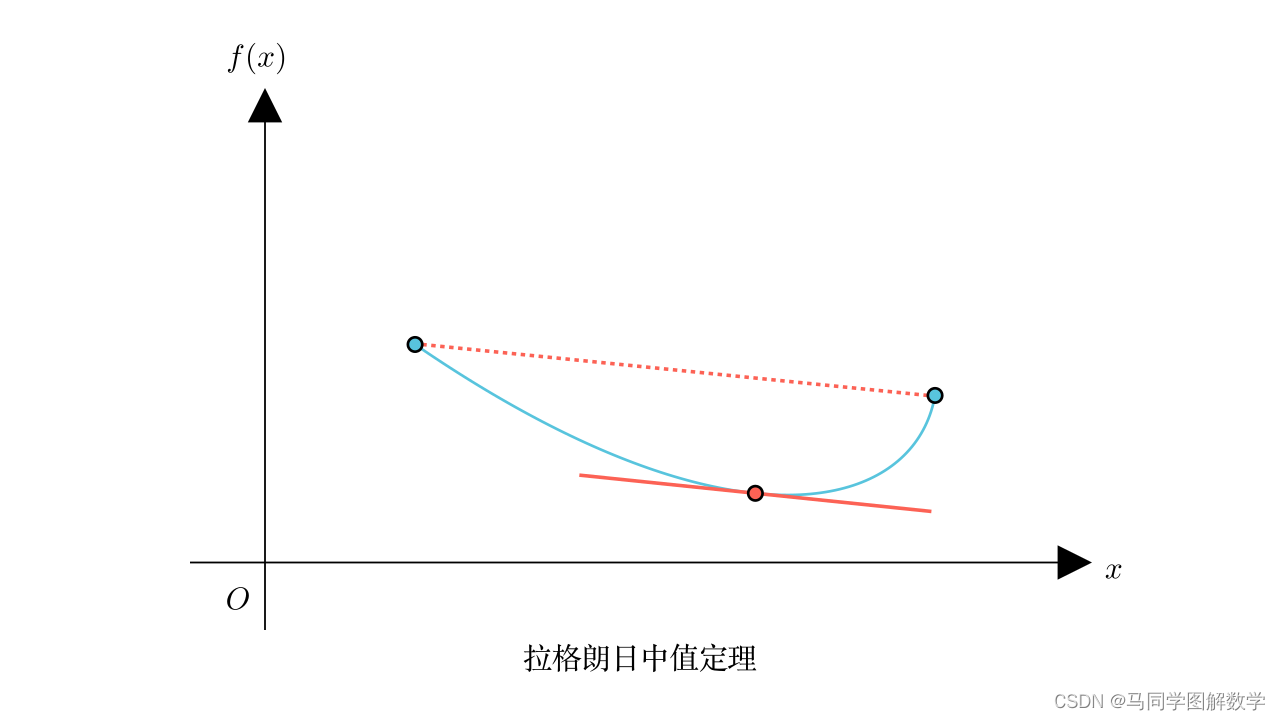
下面假设 ,那么实际上,这条曲线也可以用参数方程来表示,因此,它也是符合柯西中值定理的。
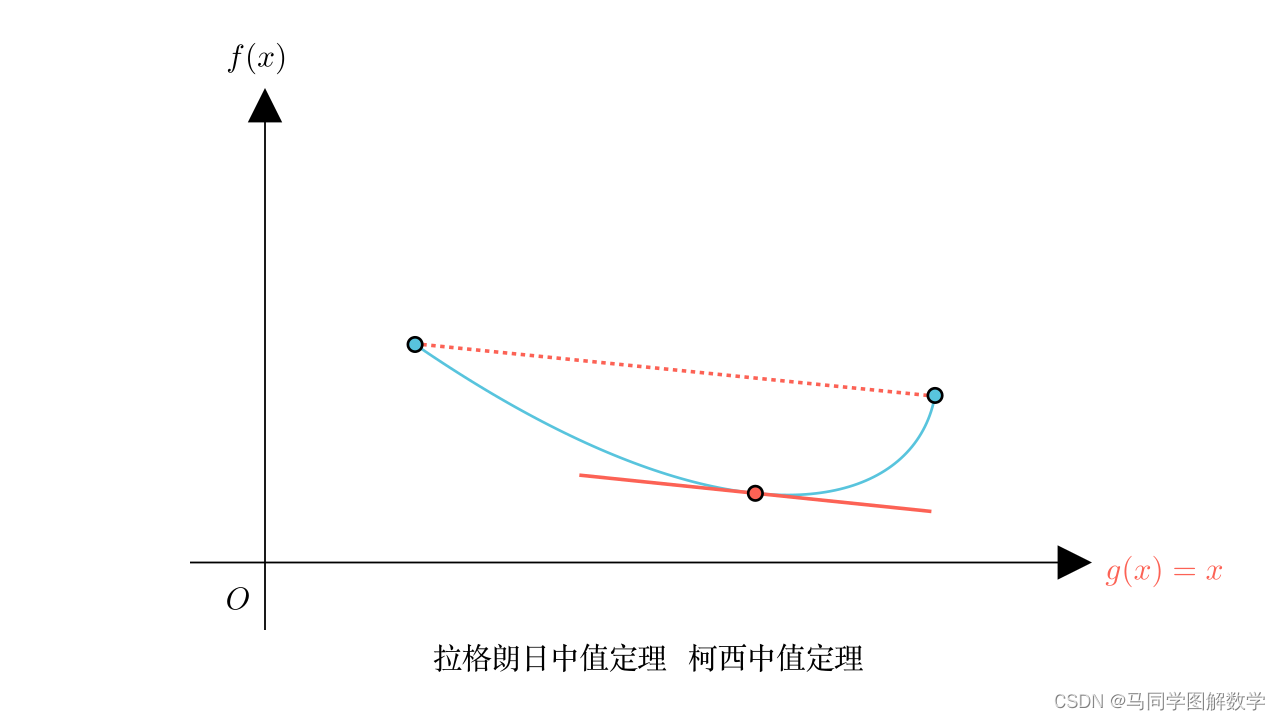
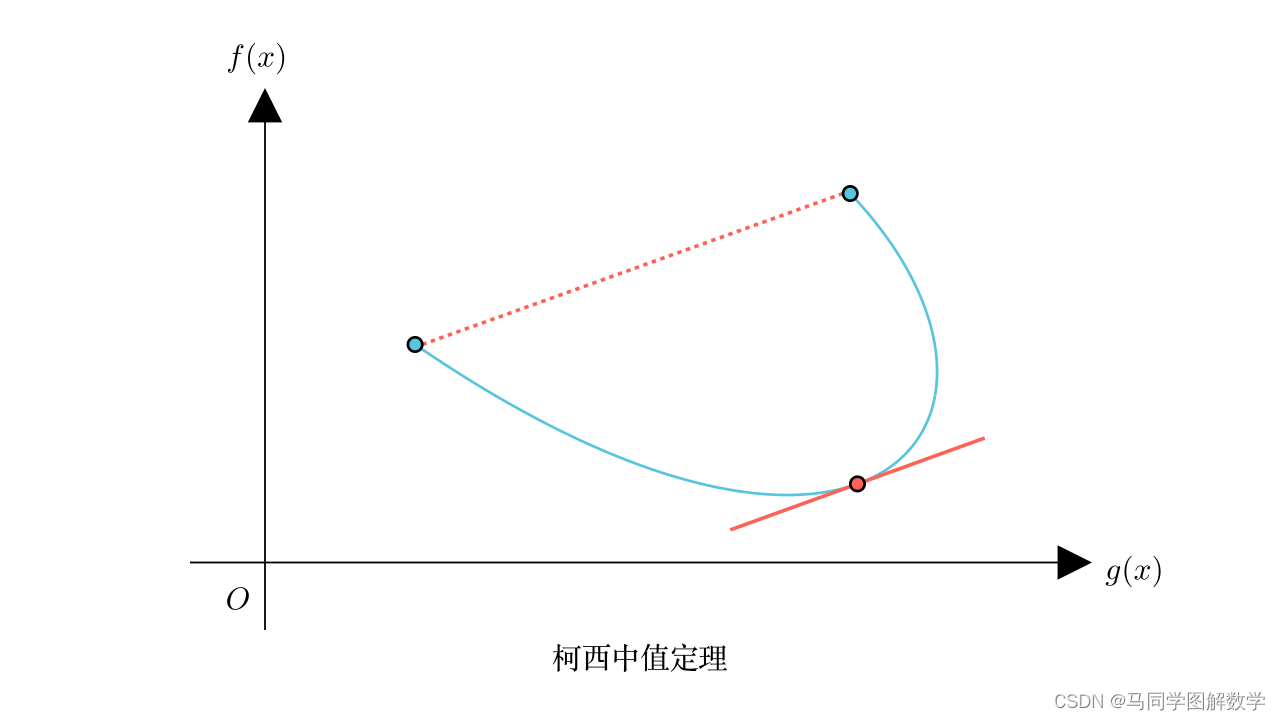
还是这条曲线,固定起点不变,对终点进行拉伸,此时,这条曲线无法再用函数表示,也就不符合拉格朗日中值定理。
现在,我们将横坐标用 表示,纵坐标用
表示,那么,它符合的是柯西中值定理。
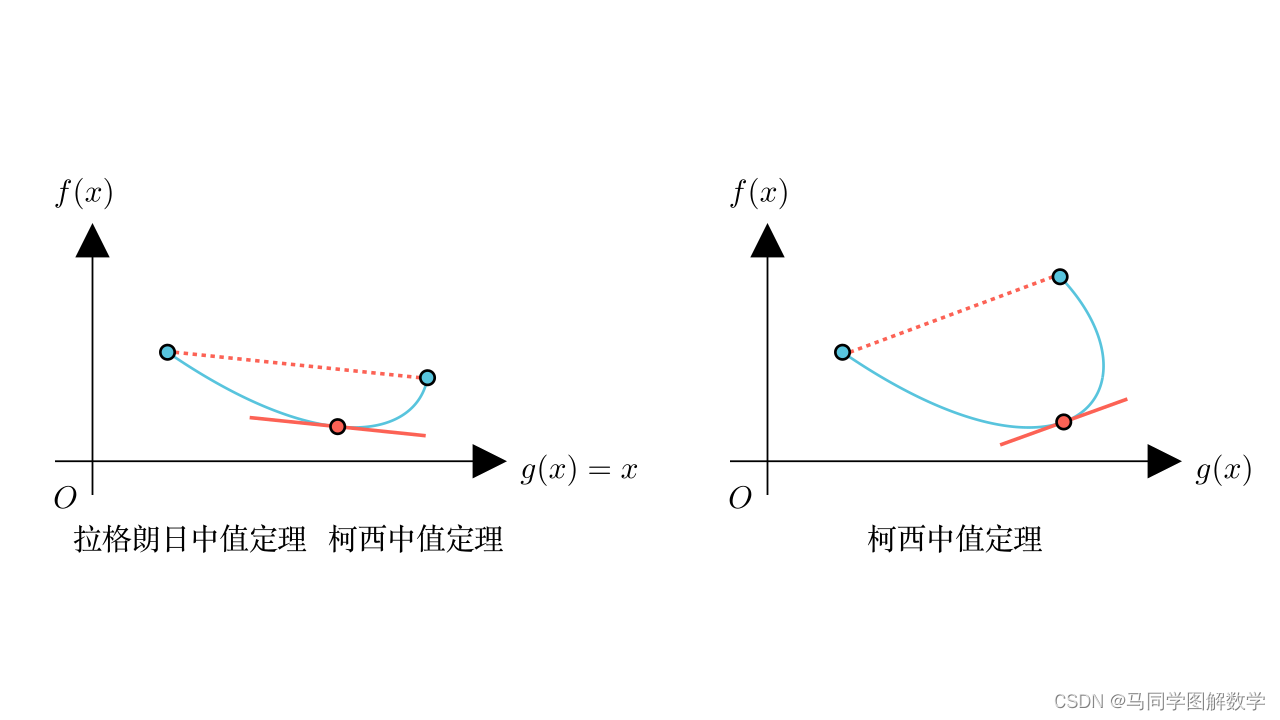
把两张图放在一起,可以很明显地看出,拉格朗日中值定理仅为 时的特殊情况。
4 证明
4.1 证明方法一
首先来看一个错误的证明方法:
由于在
上都满足拉格朗日中值定理的条件,故
,使得:
如果有
以及
,那么上述两式相除可得:
上述方法是错误的。因为对于两个不同的函数 和
,拉格朗日中值定理中的
未必相同,比如下面两个函数
-
,在
上使得拉格朗日中值定理成立的
-
,在
上使得拉格朗日中值定理成立的
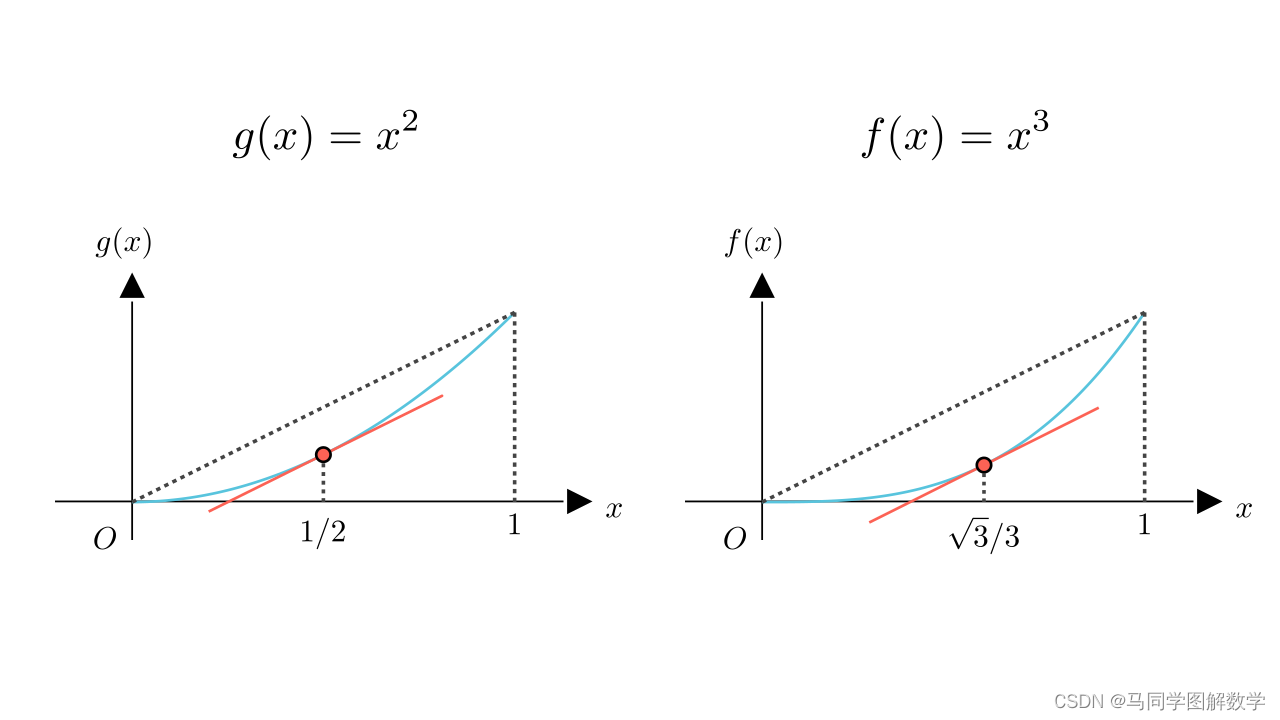
假如将函数 ,与函数
联合在一起,建立参数方程
那么,以 为横坐标,
为纵坐标建立坐标系,做出自变量在0到1范围内的参数方程图像。可以看到,当自变量取值为
时,满足柯西中值定理。
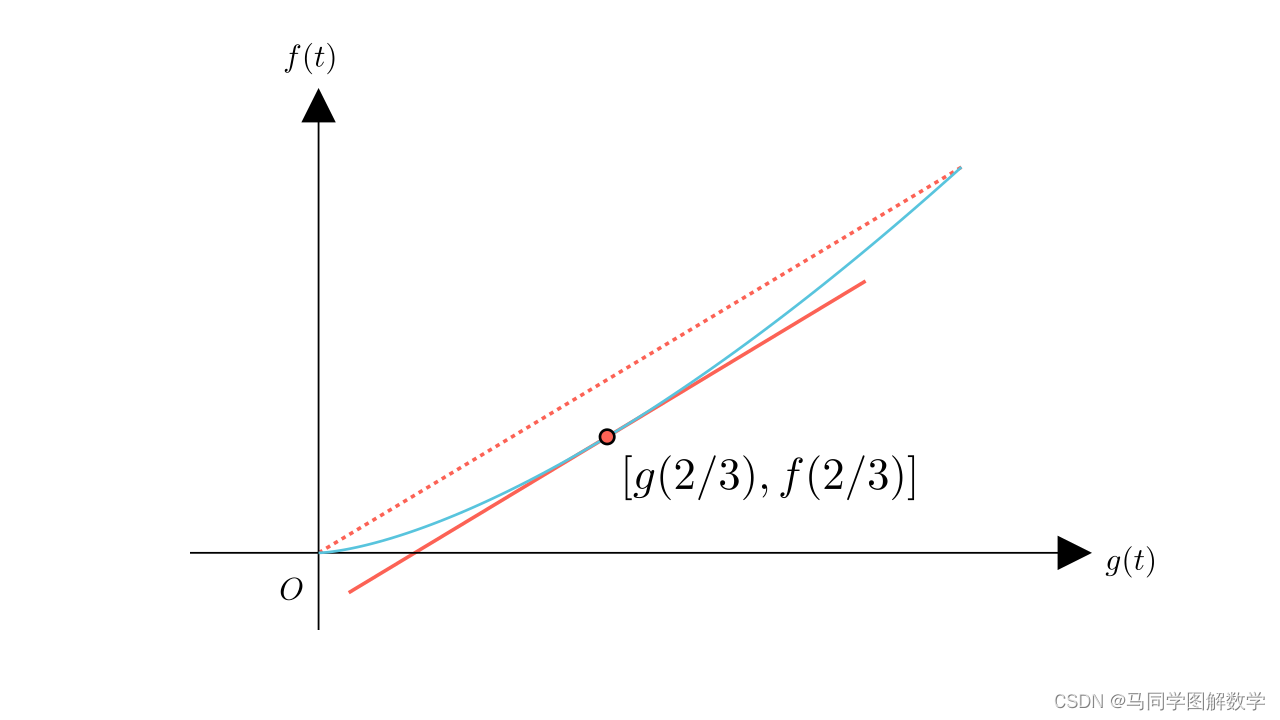
从这个例子我们就可以看出,这种方法是不正确的。
4.2 证明方法二
正确的证明方法如下:因为 ,所以构造辅助函数:
容易知道, 满足:
-
在闭区间
上连续
-
在开区间
上可导
-
所以根据罗尔中值定理, 使得
,即:
由此可得 ,如果
,那么该式可改写为
跟着马同学,看图学数学,欢迎加入马同学图解数学
马同学图解数学系列课程![]() https://matongxue.taobao.com/
https://matongxue.taobao.com/