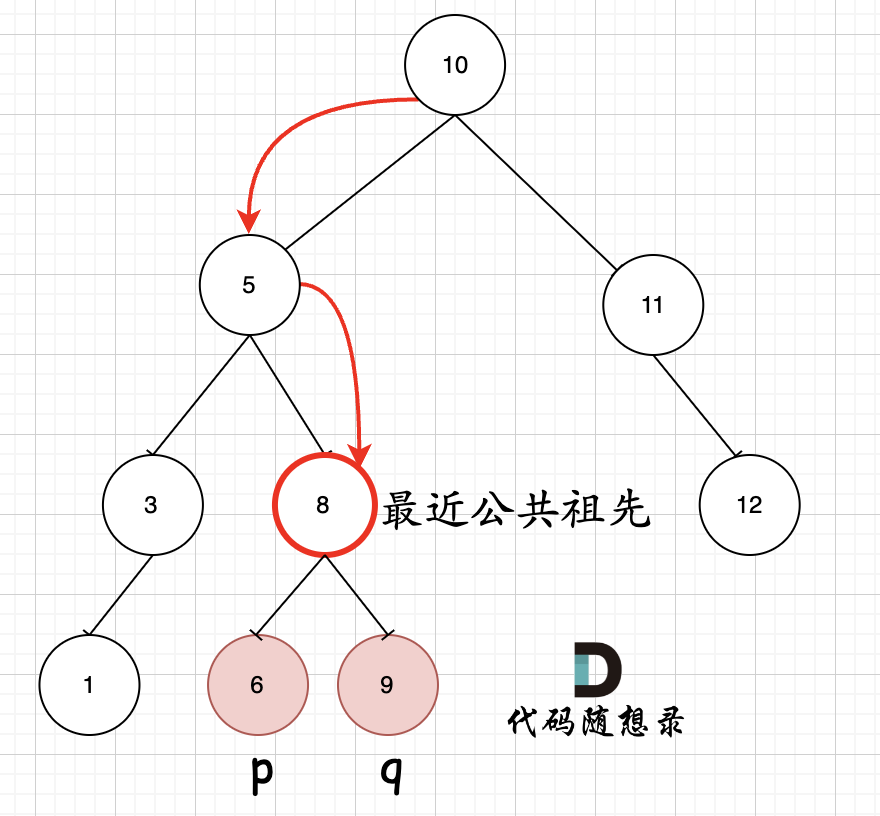
GELU是一种常见的激活函数,全称为“Gaussian Error Linear Unit”, 作为2020年提出的优秀激活函数,越来越多的引起了人们的注意。
GELU (Gaussian Error Linear Units) 是一种基于高斯误差函数的激活函数,相较于 ReLU 等激活函数,GELU 更加平滑,有助于提高训练过程的收敛速度和性能。下面是 GELU 激活层的数学表达式:
GELU表达
GELU ( x ) = x ∗ P ( X ⩽ x ) = x ∗ Φ ( x ) \operatorname{GELU}(x)=x * P(X \leqslant x)=x * \Phi(x) GELU(x)=x∗P(X⩽x)=x∗Φ(x)
其中 Φ ( x ) \Phi(x) Φ(x)表示正态分布的累积分布函数,即:
Φ ( x ) = 1 2 ⋅ ( 1 + erf ( x 2 ) ) \Phi(x)=\frac{1}{2} \cdot\left(1+\operatorname{erf}\left(\frac{x}{\sqrt{2}}\right)\right) Φ(x)=21⋅(1+erf(2x))
e r f ( x ) erf(x) erf(x) 表示高斯误差函数。
该函数可进一步表示为
x
∗
P
(
X
⩽
x
)
=
x
∫
−
∞
x
e
−
(
X
−
μ
)
2
2
σ
2
2
π
σ
d
X
x * P(X \leqslant x)=x \int_{-\infty}^x \frac{e^{-\frac{(X-\mu)^2}{2 \sigma^2}}}{\sqrt{2 \pi} \sigma} d X
x∗P(X⩽x)=x∫−∞x2πσe−2σ2(X−μ)2dX
其中 μ \mu μ和 σ \sigma σ分别代表正太分布的均值和标准差.由于上面这个函数是无法直接计算的,研究者在研究过程中发现 GELU 函数可以被近似地表示为 GELU ( x ) = 0.5 x [ 1 + tanh ( 2 π ( x + 0.047715 x 3 ) ) ] \operatorname{GELU}(x)=0.5 x\left[1+\tanh \left(\sqrt{\frac{2}{\pi}}\left(x+0.047715 x^3\right)\right)\right] GELU(x)=0.5x[1+tanh(π2(x+0.047715x3))]或者 GELU ( x ) = x ∗ σ ( 1.702 x ) \operatorname{GELU}(x)=x * \sigma(1.702 x) GELU(x)=x∗σ(1.702x)
上述表达式可以简单地通过 Python NumPy 库实现:
import numpy as np
def GELU(x):
return 0.5 * x * (1 + np.tanh(np.sqrt(2 / np.pi) * (x + 0.044715 * np.power(x, 3))))
其中 2 / π \sqrt{2 / \pi} 2/π 和 0.044715 是 GELU 函数的两个调整系数。
相较于 ReLU 函数,GELU 函数在负值区域又一个非零的梯度,从而避免了死亡神经元的问题。另外,GELU 在 0 附近比 ReLU 更加平滑,因此在训练过程中更容易收敛。值得注意的是,GELU 的计算比较复杂,因此需要消耗更多的计算资源。
GeLu和ReLu函数图像对比
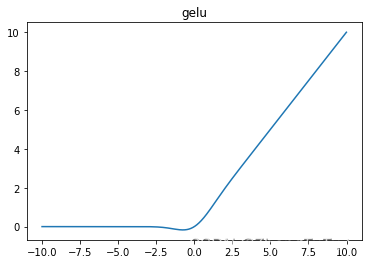
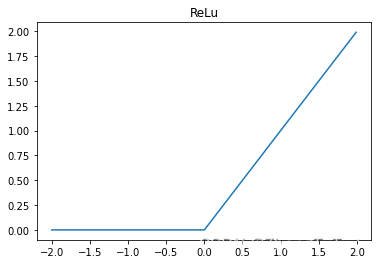
各自的优势和缺点
相对于 Sigmoid 和 Tanh 激活函数,ReLU 和 GeLU 更为准确和高效,因为它们在神经网络中的梯度消失问题上表现更好。梯度消失通常发生在深层神经网络中,意味着梯度的值在反向传播过程中逐渐变小,导致网络梯度无法更新,从而影响网络的训练效果。而 ReLU 和 GeLU 几乎没有梯度消失的现象,可以更好地支持深层神经网络的训练和优化。
而 ReLU 和 GeLU 的区别在于形状和计算效率。ReLU 是一个非常简单的函数,仅仅是输入为负数时返回0,而输入为正数时返回自身,从而仅包含了一次分段线性变换。但是,ReLU 函数存在一个问题,就是在输入为负数时,输出恒为0,这个问题可能会导致神经元死亡,从而降低模型的表达能力。GeLU 函数则是一个连续的 S 形曲线,介于 Sigmoid 和 ReLU 之间,形状比 ReLU 更为平滑,可以在一定程度上缓解神经元死亡的问题。不过,由于 GeLU 函数中包含了指数运算等复杂计算,所以在实际应用中通常比 ReLU 慢。
总之,ReLU 和 GeLU 都是常用的激活函数,它们各有优缺点,并适用于不同类型的神经网络和机器学习问题。一般来说,ReLU 更适合使用在卷积神经网络(CNN)中,而 GeLU 更适用于全连接网络(FNN)。