二叉搜索树的最近公共祖先

• 235. 二叉搜索树的最近公共祖先 - 力扣（LeetCode）

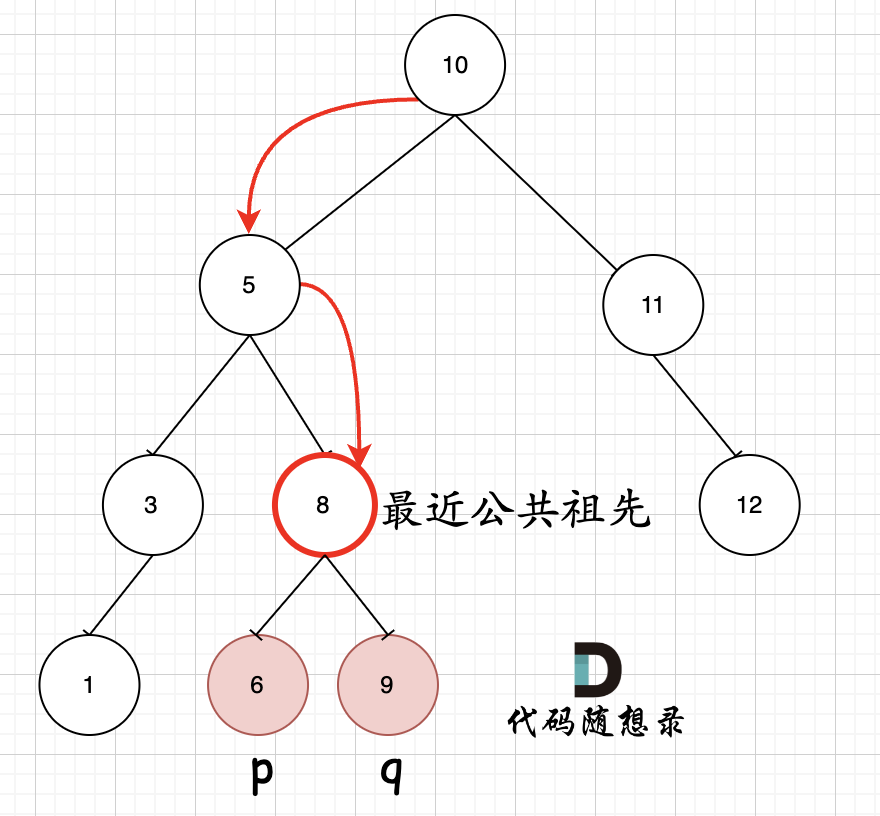
  因为二叉搜索树是有序的，第一次找到p和q中间的值，就是最近的公共祖先。

  

  class Solution {
      public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
          if(p.val > q.val){
              return traverse(root , q , p);
          }else{
              return traverse(root , p , q);
          }
      }
      TreeNode traverse(TreeNode root , TreeNode p , TreeNode q){
          if(root == null) return null;
          if(root.val >= p.val && root.val <= q.val){
              return root;
          }
          TreeNode left = traverse(root.left , p , q);
          TreeNode right = traverse(root.right , p , q);
          return left == null ? right : left;
      }
  }
  

二叉搜索树中的插入操作

• 701. 二叉搜索树中的插入操作 - 力扣（LeetCode）

  本题只需要找到空的节点进行插入即可。

  1. 通过函数的返回值，进行插入操作。

     class Solution {
         public TreeNode insertIntoBST(TreeNode root, int val) {
             
             if(root == null){
                 TreeNode node = new TreeNode(val);
                 return node;
             }
             if(root.val > val) root.left = insertIntoBST(root.left , val);
             if(root.val < val) root.right = insertIntoBST(root.right , val);
             return root;
         }
     }
     

  2. 通过保存父节点的值，进行插入操作。

     class Solution {
         TreeNode parent;
         public TreeNode insertIntoBST(TreeNode root, int val) {
             if(root == null) return new TreeNode(val);
             traverse(root , val);
             return root;
         }
         void traverse(TreeNode root , int val){
             if(root == null){
                 TreeNode node = new TreeNode(val);
                 if(parent.val > val){
                     parent.left = node;
                 }else{
                     parent.right = node;
                 }
                 return ;
             }
             parent = root;
             if(root.val > val) traverse(root.left , val);
             if(root.val < val) traverse(root.right , val);
         }
     }
     

删除二叉搜索树中的节点

• 450. 删除二叉搜索树中的节点 - 力扣（LeetCode）
  二叉搜索树的删除涉及到五个方面，尤其要注意，当删除的节点左右都有子节点时，要将左子节点放到右子节点的最左边。这才符合二叉搜索树的原则。

  class Solution {
      public TreeNode deleteNode(TreeNode root, int key) {
          //说明删除的节点不在二叉树内，直接返回null。
          if(root == null) return root;
          //root为当前要删除的节点
          if(root.val == key){
              //2：如果左右孩子都为空，直接返回null
              if(root.left == null && root.right == null){
                  return null;
              }
              //3：删除节点的左孩子为空，右孩子不为空
              else if(root.left == null){
                  //返回右孩子的根节点补位。
                  return root.right;
              }
              //4：删除节点的左孩子不为空，右孩子为空。
              else if(root.right == null){
                  return root.left;
              }
              //5：左右都不为空
              else if(root.left != null && root.right != null){
                  //找到左孩子节点
                  TreeNode left = root.left;
                  //将左孩子节点放在删除节点的右子树最左面的左孩子上。
                  TreeNode right_left = root.right;
                  while(right_left.left != null){
                      right_left = right_left.left; 
                  }
                  right_left.left = left;
                  return root.right;
              }
          }
          if(root.val > key) root.left  = deleteNode(root.left , key);
          if(root.val < key) root.right = deleteNode(root.right , key);
          //说明不是我要找的节点，返回root
          return root;
      }
  }