PL-VINS线特征处理部分源码阅读
- 1 linefeature_tracker
- 2 三角化
- 单目三角化
- 双目三角化
- 3 后端优化
- 线特征状态量
- 重投影误差
本文主要阅读PL-VINS中引入线特征的代码实现,包括线特征表示方法(Plücker参数化方法、正交表示法)、前端线特征提取与匹配、三角化、后端优化等。
公式推导参考:SLAM中线特征的参数化和求导
1 linefeature_tracker
linefeature_tracker_node的整体结构跟feature_tracker_node基本一致,主要处理在readImage,用LSD作线特征提取,LBD做描述子匹配,这部分处理都是直接调用opencv接口实现的。
LSD线特征提取
设置了一些提取参数和阈值,特别是针对线段长度做了筛选。
Ptr<line_descriptor::LSDDetectorC> lsd_ = line_descriptor::LSDDetectorC::createLSDDetectorC();
// lsd parameters
line_descriptor::LSDDetectorC::LSDOptions opts;
opts.refine = 1; //1 The way found lines will be refined
opts.scale = 0.5; //0.8 The scale of the image that will be used to find the lines. Range (0..1].
opts.sigma_scale = 0.6; //0.6 Sigma for Gaussian filter. It is computed as sigma = _sigma_scale/_scale.
opts.quant = 2.0; //2.0 Bound to the quantization error on the gradient norm
opts.ang_th = 22.5; //22.5 Gradient angle tolerance in degrees
opts.log_eps = 1.0; //0 Detection threshold: -log10(NFA) > log_eps. Used only when advance refinement is chosen
opts.density_th = 0.6; //0.7 Minimal density of aligned region points in the enclosing rectangle.
opts.n_bins = 1024; //1024 Number of bins in pseudo-ordering of gradient modulus.
double min_line_length = 0.125; // Line segments shorter than that are rejected
// opts.refine = 1;
// opts.scale = 0.5;
// opts.sigma_scale = 0.6;
// opts.quant = 2.0;
// opts.ang_th = 22.5;
// opts.log_eps = 1.0;
// opts.density_th = 0.6;
// opts.n_bins = 1024;
// double min_line_length = 0.125;
opts.min_length = min_line_length*(std::min(img.cols,img.rows));
std::vector<KeyLine> lsd, keylsd;
//void LSDDetectorC::detect( const std::vector<Mat>& images, std::vector<std::vector<KeyLine> >& keylines, int scale, int numOctaves, const std::vector<Mat>& masks ) const
lsd_->detect( img, lsd, 2, 1, opts);
LBD描述子匹配筛选
做了一个匹配筛选,认为连续两帧中,同一个线段不会发生很大的移动,所以直接比较了两个端点的像素坐标和两个线段的夹角。
Point2f serr = line1.getStartPoint() - line2.getEndPoint()这一句可能是写错了,猜测是line2.getStartPoint()
if(curframe_->keylsd.size() > 0)
{
/* compute matches */
TicToc t_match;
std::vector<DMatch> lsd_matches;
Ptr<BinaryDescriptorMatcher> bdm_;
bdm_ = BinaryDescriptorMatcher::createBinaryDescriptorMatcher();
bdm_->match(forwframe_->lbd_descr, curframe_->lbd_descr, lsd_matches);
// ROS_INFO("lbd_macht costs: %fms", t_match.toc());
sum_time += t_match.toc();
mean_time = sum_time/frame_cnt;
// ROS_INFO("line feature tracker mean costs: %fms", mean_time);
/* select best matches */
std::vector<DMatch> good_matches;
std::vector<KeyLine> good_Keylines;
good_matches.clear();
for ( int i = 0; i < (int) lsd_matches.size(); i++ )
{
if( lsd_matches[i].distance < 30 ){
DMatch mt = lsd_matches[i];
KeyLine line1 = forwframe_->keylsd[mt.queryIdx] ;
KeyLine line2 = curframe_->keylsd[mt.trainIdx] ;
Point2f serr = line1.getStartPoint() - line2.getEndPoint();
Point2f eerr = line1.getEndPoint() - line2.getEndPoint();
// std::cout<<"11111111111111111 = "<<abs(line1.angle-line2.angle)<<std::endl;
if((serr.dot(serr) < 200 * 200) && (eerr.dot(eerr) < 200 * 200)&&abs(line1.angle-line2.angle)<0.1) // 线段在图像里不会跑得特别远
good_matches.push_back( lsd_matches[i] );
}
}
vector< int > success_id;
// std::cout << forwframe_->lineID.size() <<" " <<curframe_->lineID.size();
for (int k = 0; k < good_matches.size(); ++k) {
DMatch mt = good_matches[k];
forwframe_->lineID[mt.queryIdx] = curframe_->lineID[mt.trainIdx];
success_id.push_back(curframe_->lineID[mt.trainIdx]);
}
坐标归一化
trackerData.undistortedLineEndPoints()操作后,得到当前帧下所有线特征起点和终点的归一化坐标(我感觉这个函数本意应该是要做去畸变的,结果代码里只做了像素坐标转归一化坐标,这样一来线特征不就没有去畸变吗?)
然后把id和归一化坐标pub出去
pub_img = n.advertise<sensor_msgs::PointCloud>("linefeature", 1000);
pub_match = n.advertise<sensor_msgs::Image>("linefeature_img",1000);
这版里面pub_match完全没用到啊,类比feature_tracker,猜测是留给双目显示左右目匹配用的。
2 三角化
三角化放在了里程计处理部分,一共有三种方案:
- 点特征三角化(SFM)
- 单目线特征三角化(SFM)
- 双目线特征三角化
void Estimator::solveOdometry()
{
if (frame_count < WINDOW_SIZE)
return;
if (solver_flag == NON_LINEAR)
{
TicToc t_tri;
f_manager.triangulate(Ps, tic, ric);
if(baseline_ > 0) //stereo
f_manager.triangulateLine(baseline_);
else
f_manager.triangulateLine(Ps, tic, ric);
ROS_DEBUG("triangulation costs %f", t_tri.toc());
// optimization();
onlyLineOpt(); // 三角化以后,优化一把
optimizationwithLine();
#ifdef LINEINCAM
LineBAincamera();
#else
// LineBA();
#endif
}
}
单目三角化
单目情况下线特征三角化同样是通过SFM实现。
通过ij两帧图像观测到的线段头尾端点,与当前帧相机坐标原点的连线,构造观测平面,两平面相交得到相机坐标系下的直线Lc。
分为下图两种情况:
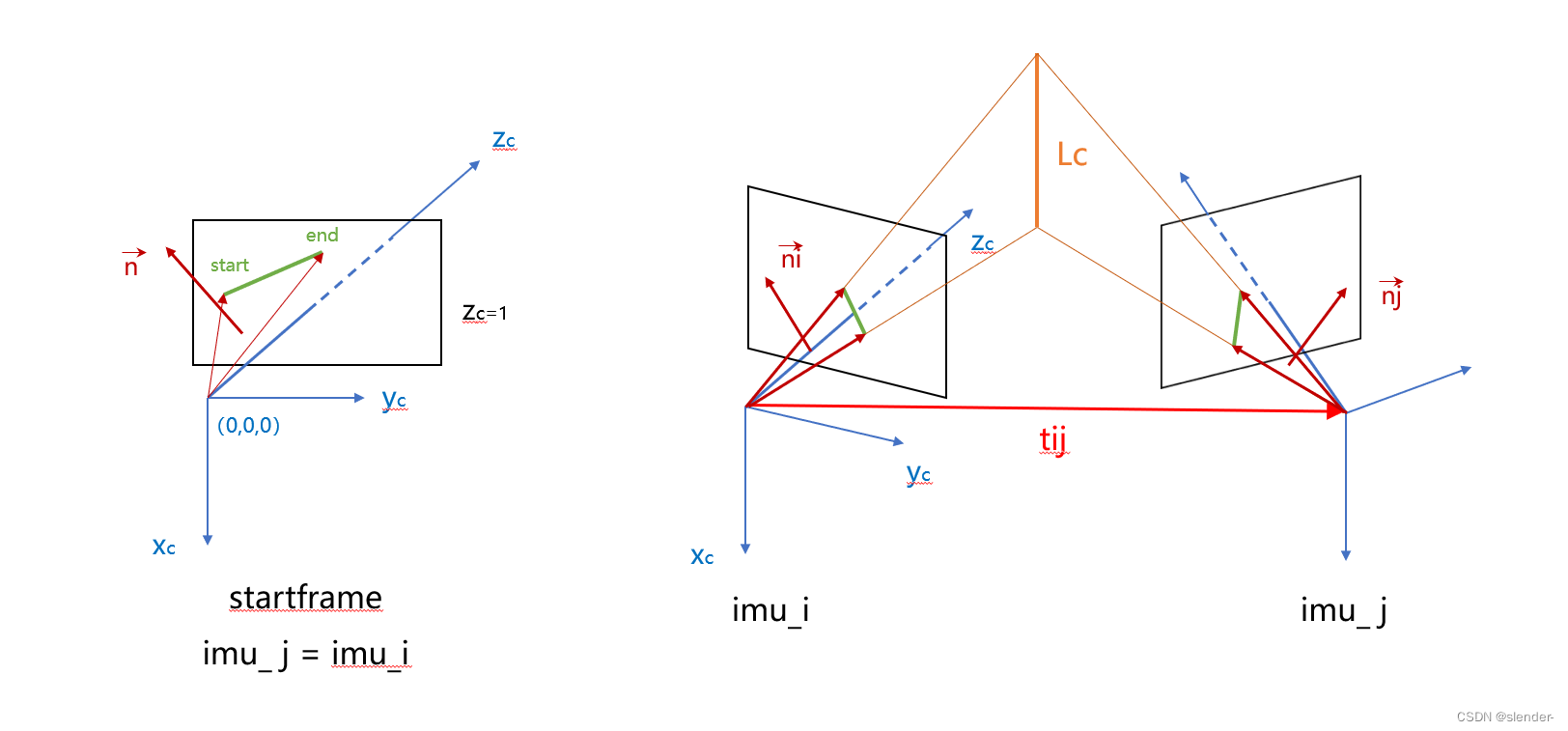
情况1:imu_j == imu_i 直接计算跟光心连线构成的平面法向量
if(imu_j == imu_i) // 第一个观测是start frame 上
{
obsi = it_per_frame.lineobs;
Eigen::Vector3d p1( obsi(0), obsi(1), 1 );
Eigen::Vector3d p2( obsi(2), obsi(3), 1 );
pii = pi_from_ppp(p1, p2,Vector3d( 0, 0, 0 ));
ni = pii.head(3); ni.normalize();
continue;
}
情况2:imu_j != imu_i 算出第i帧图像坐标系下,第j帧图像的线段与光心构成的平面法向量
// 非start frame(其他帧)上的观测
Eigen::Vector3d t1 = Ps[imu_j] + Rs[imu_j] * tic[0];
Eigen::Matrix3d R1 = Rs[imu_j] * ric[0];
Eigen::Vector3d t = R0.transpose() * (t1 - t0); // tij
Eigen::Matrix3d R = R0.transpose() * R1; // Rij
Eigen::Vector4d obsj_tmp = it_per_frame.lineobs;
// plane pi from jth obs in ith camera frame
Vector3d p3( obsj_tmp(0), obsj_tmp(1), 1 );
Vector3d p4( obsj_tmp(2), obsj_tmp(3), 1 );
p3 = R * p3 + t;
p4 = R * p4 + t;
Vector4d pij = pi_from_ppp(p3, p4,t);
Eigen::Vector3d nj = pij.head(3); nj.normalize();
两平面相交,得到相机坐标系下直线的普朗克表示
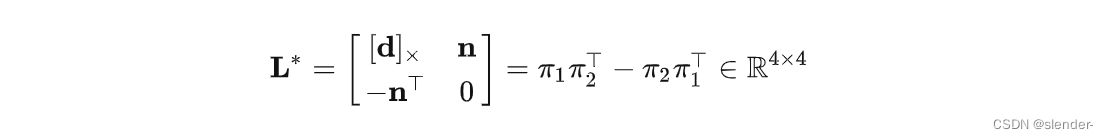
Vector6d plk = pipi_plk( pii, pij );
Vector3d n = plk.head(3);
Vector3d v = plk.tail(3);
it_per_id.line_plucker = plk; // plk in camera frame
it_per_id.is_triangulation = true;
双目三角化
双目更简单,把线段与左右目构成的平面相交。

来自论文《Building a 3-D Line-Based Map Using Stereo SLAM》
// plane pi from ith left obs in ith left camera frame
Vector3d p1( lineobs_l(0), lineobs_l(1), 1 );
Vector3d p2( lineobs_l(2), lineobs_l(3), 1 );
Vector4d pii = pi_from_ppp(p1, p2,Vector3d( 0, 0, 0 ));
// plane pi from ith right obs in ith left camera frame
Vector3d p3( lineobs_r(0) + baseline, lineobs_r(1), 1 );
Vector3d p4( lineobs_r(2) + baseline, lineobs_r(3), 1 );
Vector4d pij = pi_from_ppp(p3, p4,Vector3d(baseline, 0, 0));
Vector6d plk = pipi_plk( pii, pij );
Vector3d n = plk.head(3);
Vector3d v = plk.tail(3);
3 后端优化
做完三角化之后,先做了一次线特征的优化onlyLineOpt(),然后做了滑窗整体的优化optimizationwithLine()
- onlyLineOpt() 固定pose, 只优化line
- optimizationwithLine() 优化pose、imu、feature(points and lines)
线特征状态量
在优化部分,作者把线特征从普朗克表示(6x1)转为正交表示(4x1),在plk_to_orth 实现.
这样做主要是因为直线的自由度是4,而普朗克表示是冗余的。

引用自论文《PLS-VIO_Stereo_Vision-inertial_Odometry_Based_on_Point_and_Line_Features》

Vector4d plk_to_orth(Vector6d plk)
{
Vector4d orth;
Vector3d n = plk.head(3);
Vector3d v = plk.tail(3);
Vector3d u1 = n/n.norm();
Vector3d u2 = v/v.norm();
Vector3d u3 = u1.cross(u2);
// todo:: use SO3
orth[0] = atan2( u2(2),u3(2) );
orth[1] = asin( -u1(2) );
orth[2] = atan2( u1(1),u1(0) );
Vector2d w( n.norm(), v.norm() );
w = w/w.norm();
orth[3] = asin( w(1) );
return orth;
}
重投影误差
这里的重投影误差是把世界坐标系下的直线投影到归一化平面上,然后计算之前提取的线段两端点坐标到直线投影的距离,理想情况下是0。
注意,重投影误差是在归一化平面进行的,与相机内参无关。
ceres::LocalParameterization *local_parameterization_line = new LineOrthParameterization();
problem.AddParameterBlock( para_LineFeature[linefeature_index], SIZE_LINE, local_parameterization_line); // p,q
int imu_i = it_per_id.start_frame,imu_j = imu_i - 1;
for (auto &it_per_frame : it_per_id.linefeature_per_frame)
{
imu_j++;
if (imu_i == imu_j)
{
//continue;
}
Vector4d obs = it_per_frame.lineobs; // 在第j帧图像上的观测
lineProjectionFactor *f = new lineProjectionFactor(obs); // 特征重投影误差
problem.AddResidualBlock(f, loss_function,
para_Pose[imu_j],
para_Ex_Pose[0],
para_LineFeature[linefeature_index]);
line_m_cnt++;
}

重投影误差计算过程:
- 正交表示法→普朗克表示法
- 世界坐标系→b系→相机系→相机归一化坐标系
- 根据点到直线距离公式计算残差项
论文《PL-VIO: Tightly-Coupled Monocular Visual–Inertial Odometry Using Point and Line Features》中提到,当直线从相机系投影到归一化坐标系下,投影参数K是单位阵。
如果是投影到像素坐标系,就采用下面这个投影矩阵。

这里的[l1, l2, l3]T,就是直线参数abc,然后带入点到直线距离公式:

论文写的线段中点,代码用的起始和末尾俩端点,没啥区别。
bool lineProjectionFactor::Evaluate(double const *const *parameters, double *residuals, double **jacobians) const
{
Eigen::Vector3d Pi(parameters[0][0], parameters[0][1], parameters[0][2]);
Eigen::Quaterniond Qi(parameters[0][6], parameters[0][3], parameters[0][4], parameters[0][5]);
Eigen::Vector3d tic(parameters[1][0], parameters[1][1], parameters[1][2]);
Eigen::Quaterniond qic(parameters[1][6], parameters[1][3], parameters[1][4], parameters[1][5]);
Eigen::Vector4d line_orth( parameters[2][0],parameters[2][1],parameters[2][2],parameters[2][3]);
Vector6d line_w = orth_to_plk(line_orth);
Eigen::Matrix3d Rwb(Qi);
Eigen::Vector3d twb(Pi);
Vector6d line_b = plk_from_pose(line_w, Rwb, twb);
//std::cout << line_b.norm() <<"\n";
Eigen::Matrix3d Rbc(qic);
Eigen::Vector3d tbc(tic);
Vector6d line_c = plk_from_pose(line_b, Rbc, tbc);
// 直线的投影矩阵K为单位阵
Eigen::Vector3d nc = line_c.head(3);
double l_norm = nc(0) * nc(0) + nc(1) * nc(1);
double l_sqrtnorm = sqrt( l_norm );
double l_trinorm = l_norm * l_sqrtnorm;
double e1 = obs_i(0) * nc(0) + obs_i(1) * nc(1) + nc(2);
double e2 = obs_i(2) * nc(0) + obs_i(3) * nc(1) + nc(2);
Eigen::Map<Eigen::Vector2d> residual(residuals);
residual(0) = e1/l_sqrtnorm;
residual(1) = e2/l_sqrtnorm;
// std::cout <<"---- sqrt_info: ------"<< sqrt_info << std::endl;
// sqrt_info.setIdentity();
residual = sqrt_info * residual;
//std::cout << residual <<"\n";
if (jacobians)
{
Eigen::Matrix<double, 2, 3> jaco_e_l(2, 3);
jaco_e_l << (obs_i(0)/l_sqrtnorm - nc(0) * e1 / l_trinorm ), (obs_i(1)/l_sqrtnorm - nc(1) * e1 / l_trinorm ), 1.0/l_sqrtnorm,
(obs_i(2)/l_sqrtnorm - nc(0) * e2 / l_trinorm ), (obs_i(3)/l_sqrtnorm - nc(1) * e2 / l_trinorm ), 1.0/l_sqrtnorm;
jaco_e_l = sqrt_info * jaco_e_l;
Eigen::Matrix<double, 3, 6> jaco_l_Lc(3, 6);
jaco_l_Lc.setZero();
jaco_l_Lc.block(0,0,3,3) = Eigen::Matrix3d::Identity();
Eigen::Matrix<double, 2, 6> jaco_e_Lc;
jaco_e_Lc = jaco_e_l * jaco_l_Lc;
//std::cout <<jaco_e_Lc<<"\n\n";
//std::cout << "jacobian_calculator:" << std::endl;
if (jacobians[0])
{
//std::cout <<"jacobian_pose_i"<<"\n";
Eigen::Map<Eigen::Matrix<double, 2, 7, Eigen::RowMajor>> jacobian_pose_i(jacobians[0]);
Matrix6d invTbc;
invTbc << Rbc.transpose(), -Rbc.transpose()*skew_symmetric(tbc),
Eigen::Matrix3d::Zero(), Rbc.transpose();
Vector3d nw = line_w.head(3);
Vector3d dw = line_w.tail(3);
Eigen::Matrix<double, 6, 6> jaco_Lc_pose;
jaco_Lc_pose.setZero();
jaco_Lc_pose.block(0,0,3,3) = Rwb.transpose() * skew_symmetric(dw); // Lc_t
jaco_Lc_pose.block(0,3,3,3) = skew_symmetric( Rwb.transpose() * (nw + skew_symmetric(dw) * twb) ); // Lc_theta
jaco_Lc_pose.block(3,3,3,3) = skew_symmetric( Rwb.transpose() * dw);
jaco_Lc_pose = invTbc * jaco_Lc_pose;
//std::cout <<invTbc<<"\n"<<jaco_Lc_pose<<"\n\n";
jacobian_pose_i.leftCols<6>() = jaco_e_Lc * jaco_Lc_pose;
//std::cout <<jacobian_pose_i<<"\n\n";
jacobian_pose_i.rightCols<1>().setZero(); //最后一列设成0
}
if (jacobians[1])
{
//std::cout <<"jacobian_ex_pose"<<"\n";
Eigen::Map<Eigen::Matrix<double, 2, 7, Eigen::RowMajor>> jacobian_ex_pose(jacobians[1]);
Vector3d nb = line_b.head(3);
Vector3d db = line_b.tail(3);
Eigen::Matrix<double, 6, 6> jaco_Lc_ex;
jaco_Lc_ex.setZero();
jaco_Lc_ex.block(0,0,3,3) = Rbc.transpose() * skew_symmetric(db); // Lc_t
jaco_Lc_ex.block(0,3,3,3) = skew_symmetric( Rbc.transpose() * (nb + skew_symmetric(db) * tbc) ); // Lc_theta
jaco_Lc_ex.block(3,3,3,3) = skew_symmetric( Rbc.transpose() * db);
jacobian_ex_pose.leftCols<6>() = jaco_e_Lc * jaco_Lc_ex;
jacobian_ex_pose.rightCols<1>().setZero();
}
if (jacobians[2])
{
Eigen::Map<Eigen::Matrix<double, 2, 4, Eigen::RowMajor>> jacobian_lineOrth(jacobians[2]);
Eigen::Matrix3d Rwc = Rwb * Rbc;
Eigen::Vector3d twc = Rwb * tbc + twb;
Matrix6d invTwc;
invTwc << Rwc.transpose(), -Rwc.transpose() * skew_symmetric(twc),
Eigen::Matrix3d::Zero(), Rwc.transpose();
//std::cout<<invTwc<<"\n";
Vector3d nw = line_w.head(3);
Vector3d vw = line_w.tail(3);
Vector3d u1 = nw/nw.norm();
Vector3d u2 = vw/vw.norm();
Vector3d u3 = u1.cross(u2);
Vector2d w( nw.norm(), vw.norm() );
w = w/w.norm();
Eigen::Matrix<double, 6, 4> jaco_Lw_orth;
jaco_Lw_orth.setZero();
jaco_Lw_orth.block(3,0,3,1) = w[1] * u3;
jaco_Lw_orth.block(0,1,3,1) = -w[0] * u3;
jaco_Lw_orth.block(0,2,3,1) = w(0) * u2;
jaco_Lw_orth.block(3,2,3,1) = -w(1) * u1;
jaco_Lw_orth.block(0,3,3,1) = -w(1) * u1;
jaco_Lw_orth.block(3,3,3,1) = w(0) * u2;
//std::cout<<jaco_Lw_orth<<"\n";
jacobian_lineOrth = jaco_e_Lc * invTwc * jaco_Lw_orth;
}
}
这里还有一个要留意的点,在计算点到直线距离的时候,直线abc参数直接就是法向量参数。
光心与相机坐标系下的线特征两端连线,构成一个平面并且得到这个平面的法向量。那为什么这个法向量就是归一化平面上投影直线的参数呢?
法向量n=[n1, n2, n3],对于投影直线上的一个点(x, y, z), 这个点位于归一化平面上z=1,同时位于法向量所在平面上,所以就有 n1x+n2y+n3=0,对应了直线表达式 ax+by+c=0。
这也解释了为什么投影矩阵为单位阵,它的投影过程只与法向量有关,在这个过程中法向量并不发生变化。