1. 对折

这个大家可以自己用纸对折一下，我这里就简单的说一下：

这是我们第一次对折的情况。然后我们进行第二次对折：

这是我们第二次对折，我们再第三次对折：

如果我们把它转换成树的形状，我们可以这样：

如果我们想从上到下打印，其实就是中序遍历。

代码实现
从上图中我们可以发现一些规则：1. 头结点的凹的。2. 所有左子树的根是凹的，所有右子树的根是凸的。3. 对折几次就有几层。

这个打印函数第一个参数说明当前是第几层，第二个参数是对折了几次(总共有几层)，第三个参数意思是：当前结点的凹的话，down=true，如果是凸的话，down=false。

如果i>N的话说明超过了总层数，就返回。
我们先往左边递归，当递归到左边最后一个的时候，返回，然后打印此时的down。再往右边递归，形成一个中序遍历。

2. 判断是否是平衡二叉树

难度 简单 题目链接

解题思路：
我们要判断一棵树是否是平衡二叉树，我们就要用一些变量来记录它的状态。在平衡二叉树中，我们可以用高度来衡量。
第一步：我们用结构体先定义一个信息体。

一个记录当前结点的高度，一个记录这个树是否平衡。

第二步：判断是不是空树。

如果是空树，我们就返回true，高度为0。不为空，就递归到左子树和右子树。

第三步：递归回来，判断此树是否为平衡二叉树。

我们先认为它是平衡的，如果子树不满足条件的话，就设置成false。然后返回此树的一个情况。

在主函数直接返回这个树的一个平衡状态就行了。

3. 判断是否是搜索二叉树

难度 中等 题目链接

解题思路：
那么我们要判断是否是搜索二叉树，也可以定义一个信息体来记录一些条件信息。这里，我们要找左子树的最大值和右子树的最小值。但是递归需要传递的信息是一样的，所以不论是左子树还是右子树，我们都把两边的最小值和最大值找出来。


这里空树不知道返回什么，我们就返回空。然后返回到上层的时候，再做处理。当递归回来的时候，我们就要判断当前结点为根的树是否是搜索二叉树：

然后，我们再把以当前结点为根的树的最大值和最小值算出来返回。

4. 二叉树的直径

难度 简单 题目链接

示例：

这道题首先分几种情况：
第一种情况：和根结点无关

这种情况最大距离是在左子树或右子树中。

第二种情况：和根结点有关

这种情况的最大距离是：左子树的高度+右子树的高度。

代码实现：

首先还是先构造出信息体：最大距离和高度

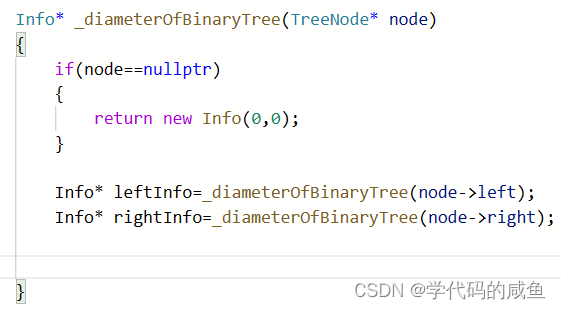
当递归回来时，我们判断三种可能性：

选出这三种可能性最大的那个：

最后把max和高度求出来，然后返回：

5. 寻找最大二叉搜索树

这道题是什么意思，举个例子大家看一下：

这样的一个树，它自己本身不是一颗搜索二叉树，但是它的左子树和右子树是搜索二叉树，它的左子树的结点是4，右子树的结点是3。所以最大搜索二叉树结点个数就是4。

解题思路：
情况一：最大二叉搜索树不是以此结点为根
那么最大二叉搜索树就在此结点左子树或右子树中。

情况二：最大二叉搜索树是以此结点为根
那么我们首先要判断：
1.左子树和右子树是否是二叉搜索树。
2.左子树的max<x，右子树的min>x。
3.左子树的size+右子树的size+自己

下面我们可以创建一个信息体：

这里的第一个其实可以省略，如果整棵树的个数和最大二叉搜索树的个数相等，就说明此树是二叉搜索树。我们就可以简写：

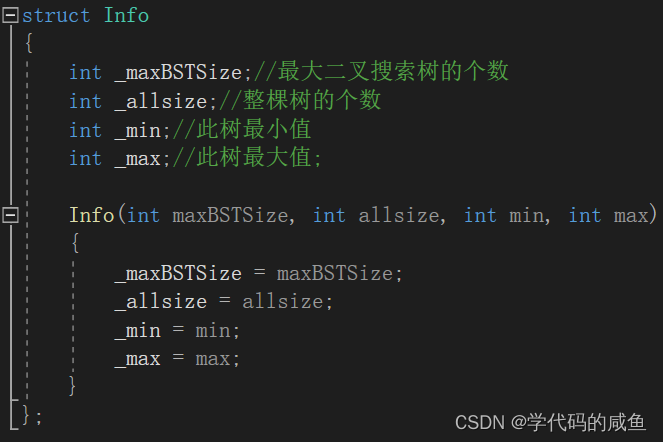
然后继续按照之前的套路：

当递归回来时，我们把以此根为树的四个信息计算出来，然后返回。

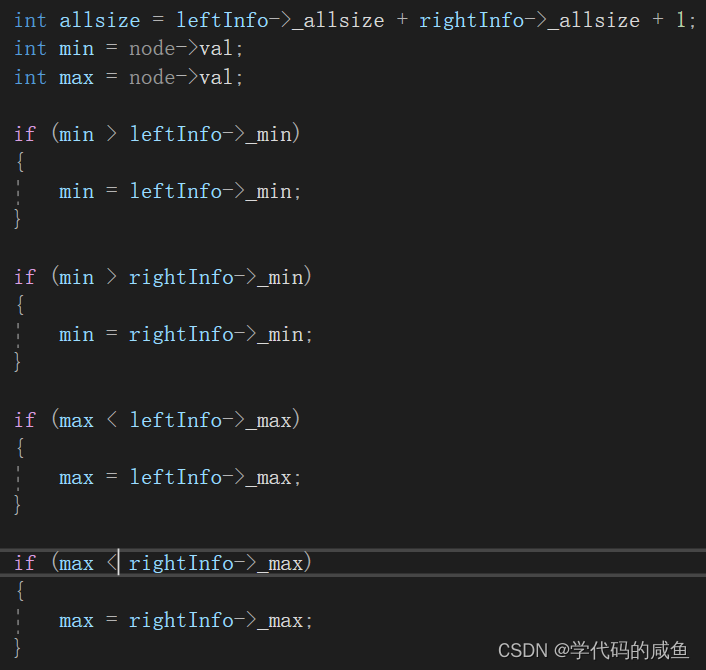
这三个信息比较简单，我们还差最大二叉搜索树的个数：

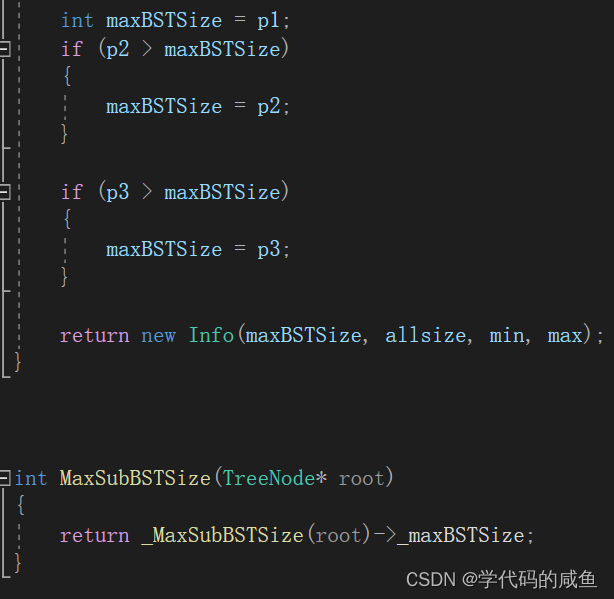
然后比较这三种情况，最大的返回。

6. 用递归套路判断是否是完全二叉树

难度 中等 题目链接

那么我们首先还是要把所有的可能性列举出来：
第一种情况：左子树是满二叉树，右子树是满二叉树，左子树高度==右子树高度。

第二种情况：左子树是完全二叉树，右子树是满二叉树，左子树高度=右子树高度+1。

第三种情况：左子树是满二叉树，右子树是满二叉树，左子树高度=右子树高度+1。

第四种情况：左子树是满二叉树，右子树是完全二叉树，左子树高度==右子树高度。

还是和前面一样，先写信息体：

然后就按照我们之前分析的情况来判断：

7. 派对的最大快乐值

题目：
一个公司现在要办party，你可以决定哪些员工来，哪些员工不来。
规则：
1.如果某个员工来了，那么这个员工的所有下级都不能来。
2.派对的整体快乐值是所有到场员工快乐值的累加。
3.你的目标是让派对的整体快乐值最大。

给定一棵多叉树的头节点boss，请返回派对的最大快乐值。

公司的每个员工都符合Employee类的描述。整个公司的人员结果可以看作是一颗标准的，没有环的多叉树。树的头结点是公司唯一的老板。除老板之外的每个员工都有唯一的直接上级。叶结点是没有任何下属的基层员工，除基层员工外，每个员工都有一个或多个直接下级。

员工信息的定义如下：

//员工的信息定义
struct Employee
{
	int _happy;//这名员工可以带来的快乐值
	list<Employee> subordinates;//这名员工的直接下级
};

举个例子：

这是一颗多叉树，如果我们选了第一层的结点，第二层就不能选，但是可以选第三层。如果我们选择了第二层，就不能选第一层和第三层了。然后，根据这样的规则把选出所有人的最大值找出。

首先，我们分析可能性：
第一种情况：根结点来。
根结点的happy值+下级成员不来的最大值

这里的意思就是x的happy+a不来的最大happy+a不来最大happy值+a不来最大happy值+c不来最大happy值。

第二种情况：根结点不来。
把下级成员来的happy值和不来的happy值进行比较，选出最大的

这个意思是max(a来，a不来)+max(b来，b不来)+max(c来，c不来)。

代码实现：
那么我们就先写信息体：其实就两个，来的最大值和不来的最大值。

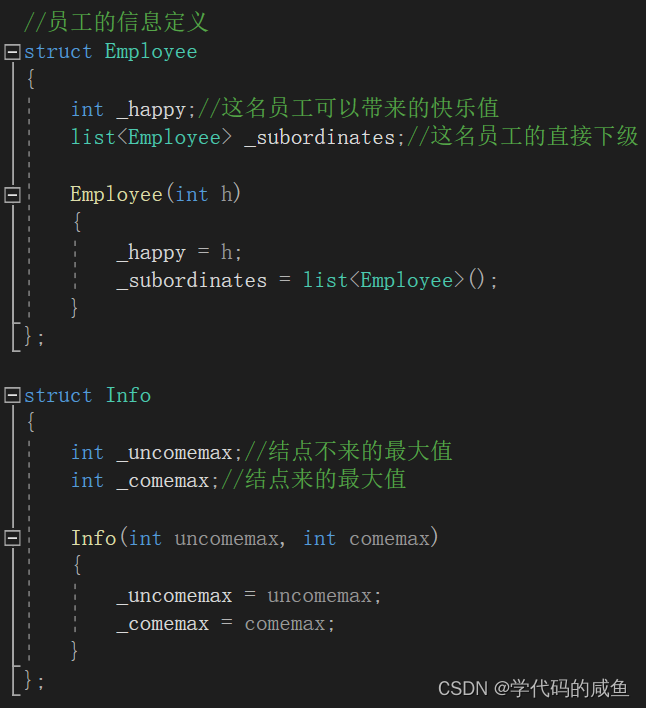
然后我们就需要写递归体：

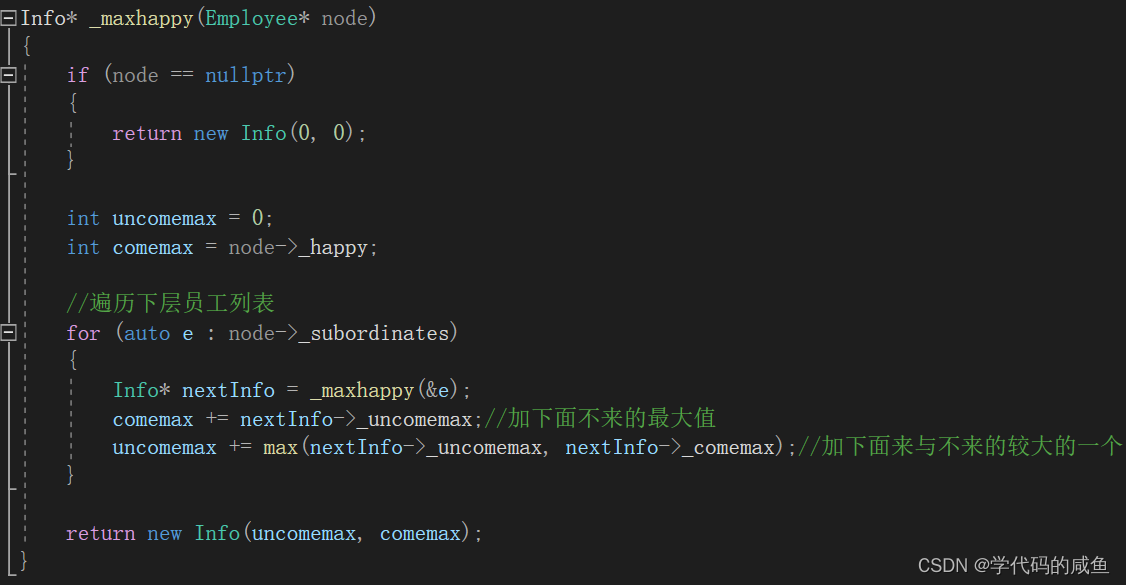
这里是先遍历当前结点的所有下级员工，然后递归下去，把最下面一层的员工来与不来的最大值算出。然后就会递归上去，再统计出。

最后就得出答案。