Matlab群体智能优化算法之巨型睡莲优化算法(VAO)

摘要：介绍一种新型智能优化算法，巨型睡莲优化算法。其应用于24个基准测试函数，并与其他10个著名算法进行了比较。提出的算法在10个优化问题上进行了测试：最小生成树、枢纽位置分配、二次分配、聚类、特征选择、回归、经济调度、并行机器调度、颜色量化和图像分割，并与传统算法和生物启发算法进行了比较。总体而言，该算法在所有任务中的表现都令人满意。参考文献：Mousavi S M H. Victoria Amazonica Optimization (VAO): An Algorithm Inspired by the Giant Water Lily Plant[J]. arXiv preprint arXiv:2303.08070, 2023.

注：

• 仅记录学习过程，如有侵权，联系删除
• 本文所用墨滴模板为slandarer创作

灵感来源

维多利亚亚马逊植物，通常呗称为巨型睡莲，拥有世界上最大的浮动球形叶片，最大叶片直径为3米。它通过其刺的力量传播叶子，并在下面形成一个大阴影，杀死任何需要阳光的植物。这些水霸用他们强大的刺迫使每一个浮出水面，并增加他们的力量，从水面攫取更多空间。当它们蔓延到整个池塘或盆地时，最早胜场的叶子有更多的生长空间，每片叶子都获得独特的大小。它的花是变性的，当它们开花时，甲虫负责授粉过程，被雌花的气味吸引。进入花朵后，甲虫身上沾满了花粉，并将其转移到另一朵花上受精。甲虫离开后，花变成了雄花，颜色从白色变成粉红色。雄花死亡并沉入水中，释放出它的种子，帮助创造新的一代。

在作者提出的算法中，介绍了这种壮丽植物的数学生命周期，每片叶子和花朵都被当作一个实体。

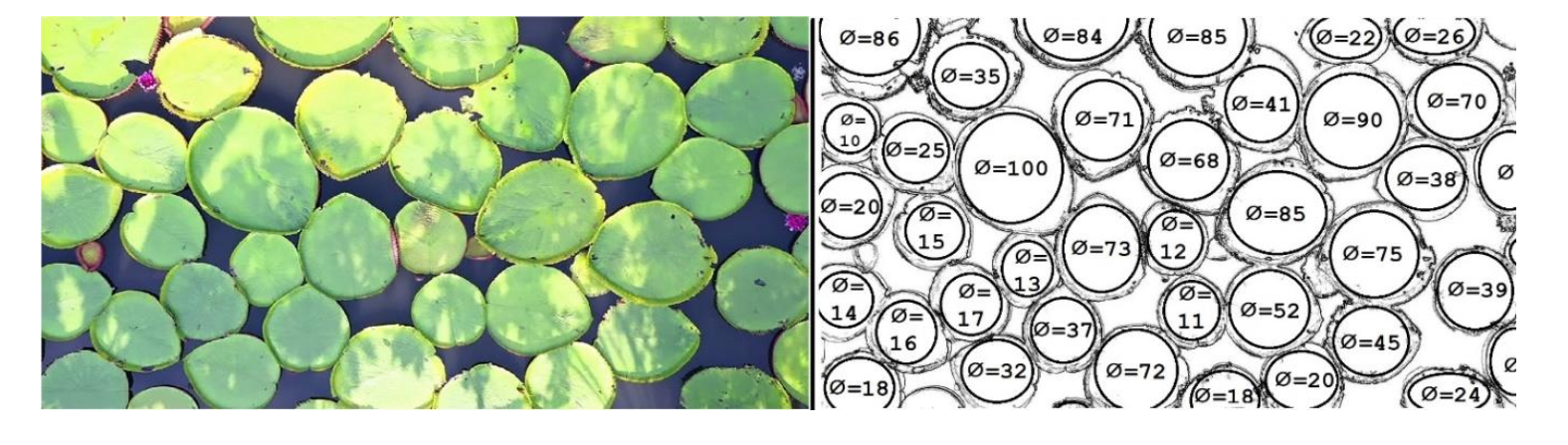
第二幅图，直径写10-100形象的比喻一下传播力，并不是直径100米。

VAO算法

VOA算法关注的是初始种群(叶子和花)的分布以及它们在表面上响应的传播力。该算法主要是一种基于蜂群局部搜索的元启发式算法，因此唯一的缺点是有可能陷入局部最优。

下面介绍一下算法中涉及的各个字母的含义

• $\phi $ ：直径
• $\lambda$ ：优化任务，本质上就是让直径越来越大。睡莲通过用上升的力量和脊柱强行置换彼此所能获得的空间大小，从而增大其直径。这种竞争被成为内部竞争，用$\lambda$表示。
• $\omega $：睡莲生长存在三个常见的困难。花内甲虫的死亡，甲虫不受粉或者授粉不当，以及温度降低。所有这些因素都有可能对这个过程不利，我们在这里把它们都成为$\omega $。显然，$\omega $的值越大，表明植物越弱。
• $\psi$ ：害虫，如睡莲蚜虫，也可以通过吃植物的叶子和在叶子上制造洞来伤害植物。本文用$\psi$来代表这种威胁值。$\psi$的值越低，对植物生长和扩张越有利。
• $\mu$：最后，当池塘里的甲虫用另一种睡莲给花授粉时，就会发生突变。这种现象被成为“杂交突变”，用$\mu$表示。这种突变可以在正反两个方向上发生，每一代的比率为0.2%。
• $\alpha$：最大和最强的叶子时最好的，用$\alpha$表示。

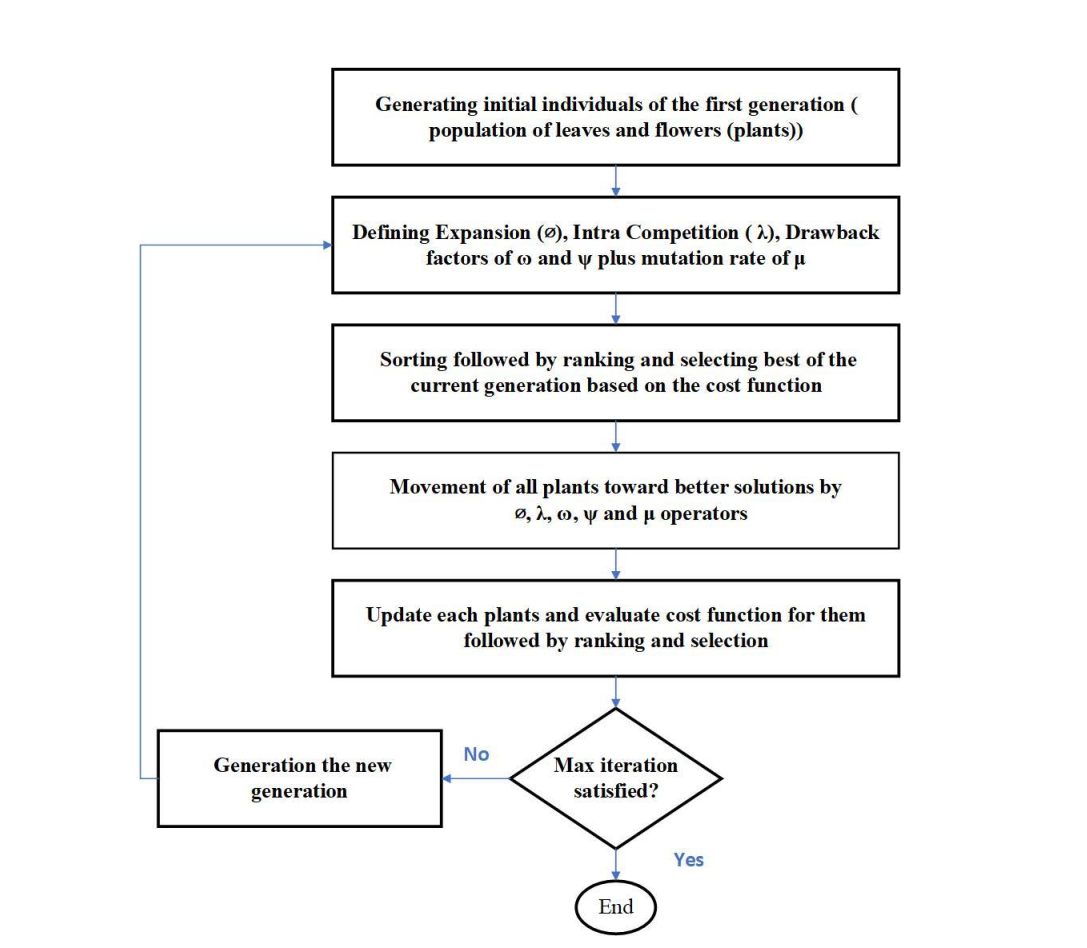
伪代码

$$VAO=\sum _{i=1}^n\sum _{j=1}^n(xij[\varnothing ij,\lambda \mathrm{ij}]+\psi +\omega )\ast (\mu )$$

在上述公式中，可以明确看出，直径，内部竞争，困难，威胁，突变五个参数的影响

---

产生种群，定义每个个体的直径，定义内部竞争，定义困难和威胁，二者随机范围都在[0.1,0.3],变异概率是一个0.2。
终止循环的条件是迭代次数。在每一次的迭代过程中，首先比较每个睡莲的直径或者内部竞争，一直更新最大的；其次，变异作用一下；再次；困难和威胁作用；从次，计算适应度值；最后排序并且找到最好的。

• 加粗字体：MATLAB
• 斜体：MATLAB

评价和结果

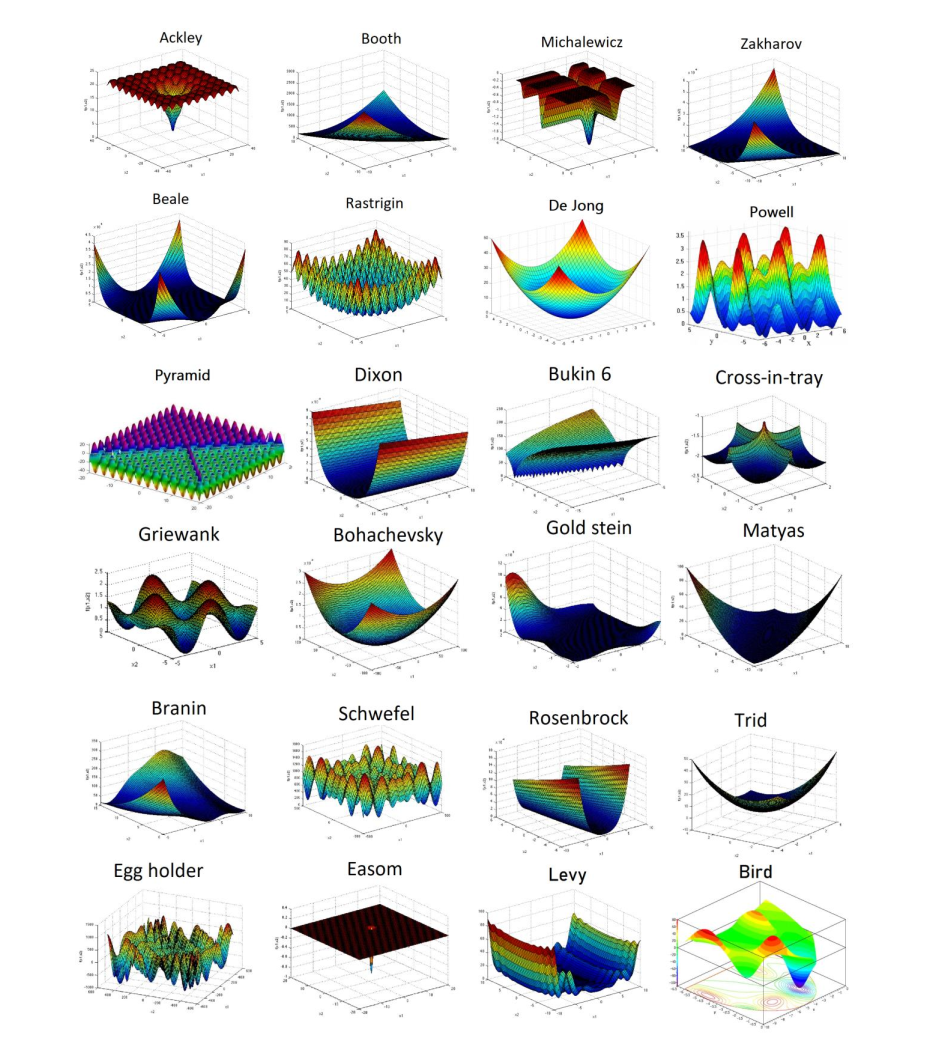
本文不在此列出详细绘制这种三维图，网上这种代码很多，大家也可以参考原文，然后自己写代码。
可以在下述链接中找到这些函数的代码。
http://www.sfu.ca/~ssurjano/index.html

在作者提供的源代码中，和现在所看到的公式有所不一样。在位置更新上，所用公式并不是文中提到的公式。除此之外，他还有一个合并和排序更新，这个类似于反向学习的思路，假如原来有20个睡莲，在经过公式更新后，就会变成40个，然后对这40个进行排序，取前20个睡莲。他还有一个突变系数阻尼比，这个其实可以理解，不能一直在突变，突变的概率会越来越小的。这个系数给的是0.98，也就是0.2*0.98，依次类推。

在此给出更新公式：
KaTeX parse error: Expected 'EOF', got '_' at position 11: \text{new_̲x}=x_i+\psi * e…

仔细看看这个公式，核心部分在第二部分和第三部分，第二部分包含了困难威胁内部竞争三个参数。
其中，$\Delta =0.05\ast (VarMax-VarMin)$;
$\mu =\mu \ast {\mu }_{damp}$;
${\mu }_{damp}=0.98$

基本测试函数的测试（此处只给一例，Ackley函数）

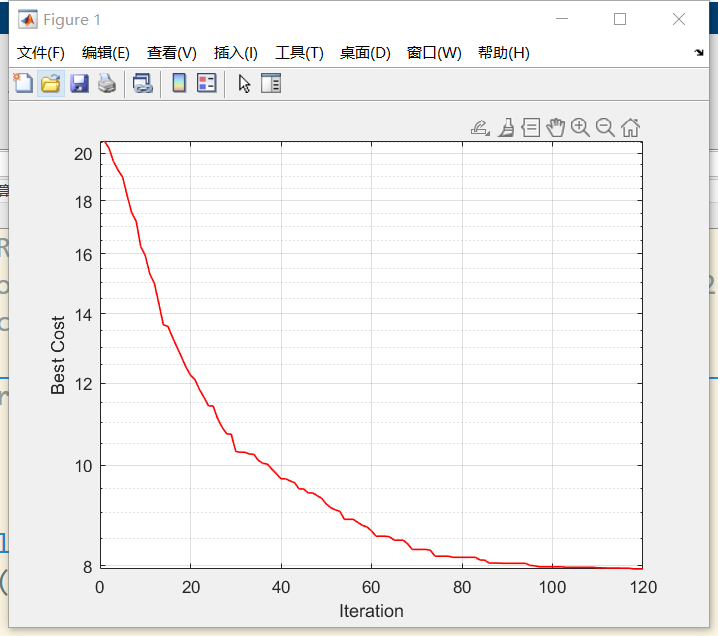
Ackley函数，给了一个睡莲的分布图，和原文中的图9应该是对应的。

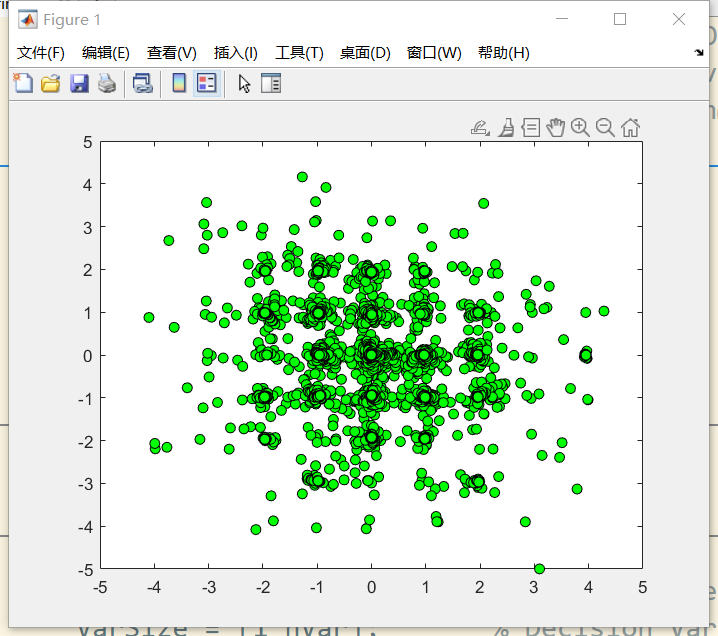
没看明白这个的意义。不如画一个三维的动态图，去看睡莲的走向。这个图，作者应该是想体现能找到最优的那个点吧。不是很理解。

鸢尾花分类测试

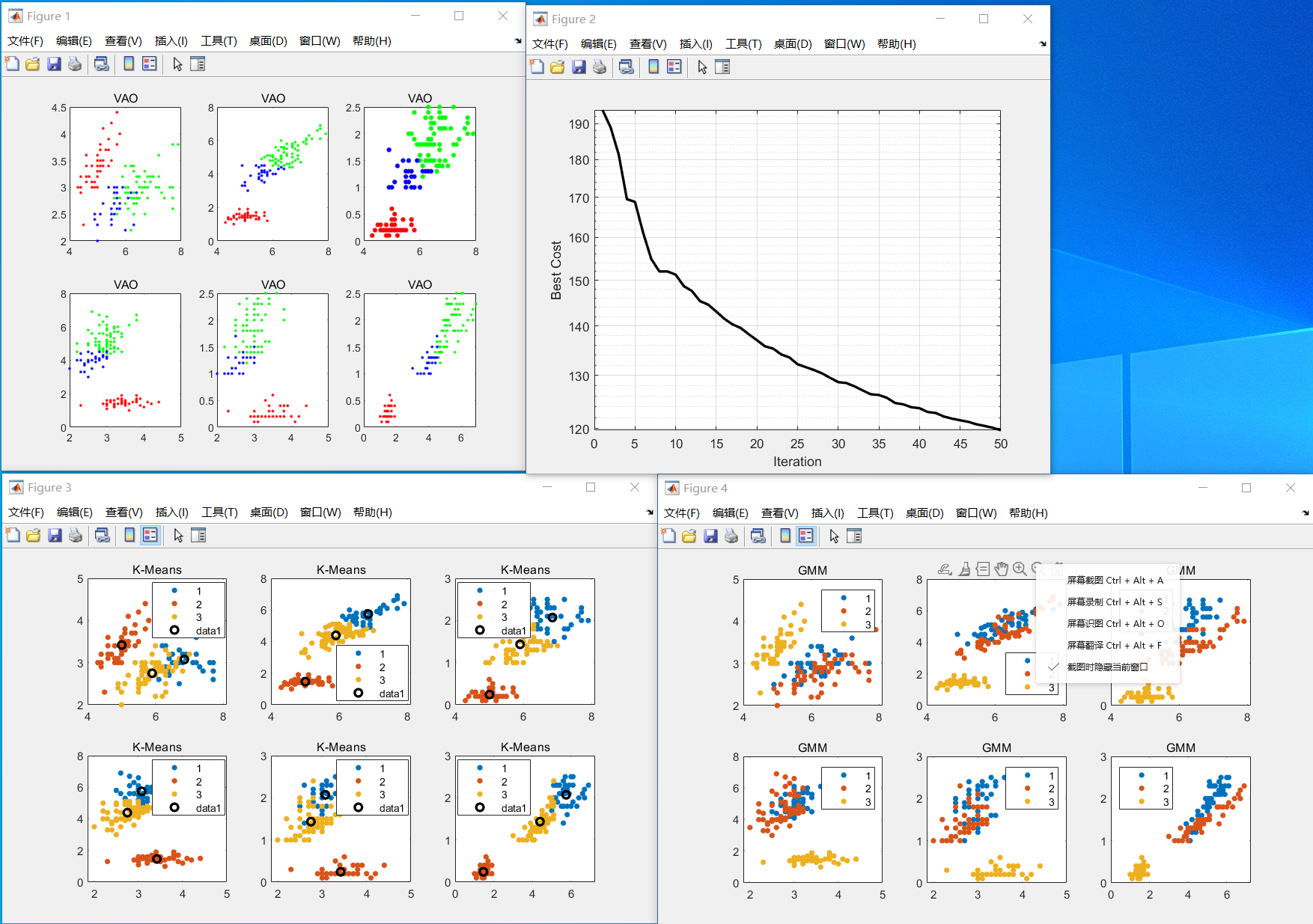
作者给出了十个测试问题的代码，感兴趣的可以自己试试。

再次提醒大家，所有的代码都是作者开源的。不要购买任何这种别人提出来的什么算法代码，这代码在mathworks上都是免费下载的。或者去github上下载。

在这给出枢纽位置分配的测试结果。30个位置选5个枢纽

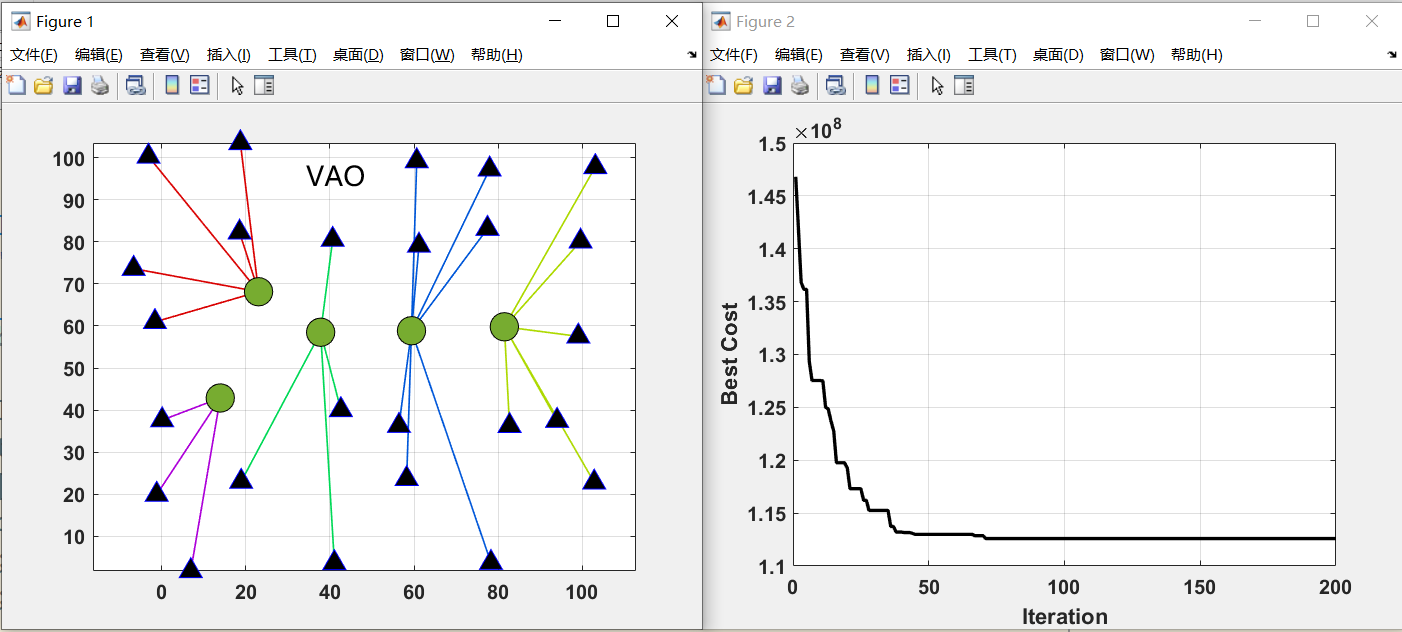
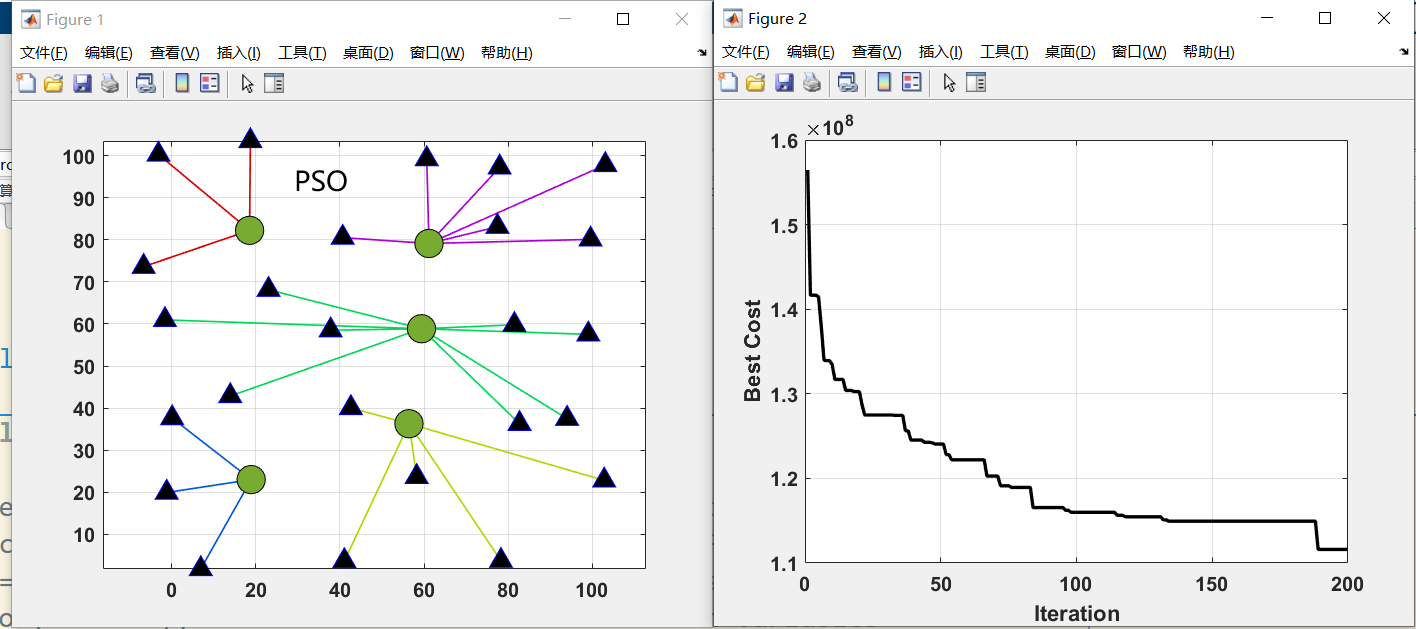
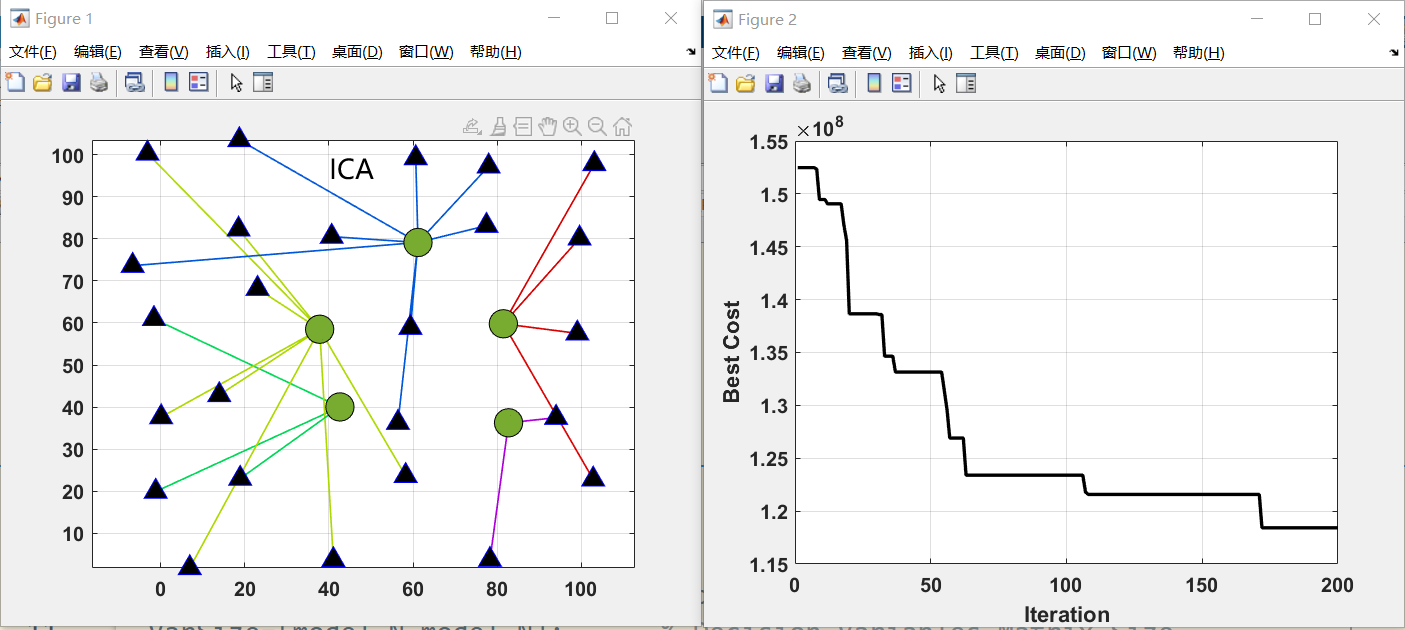
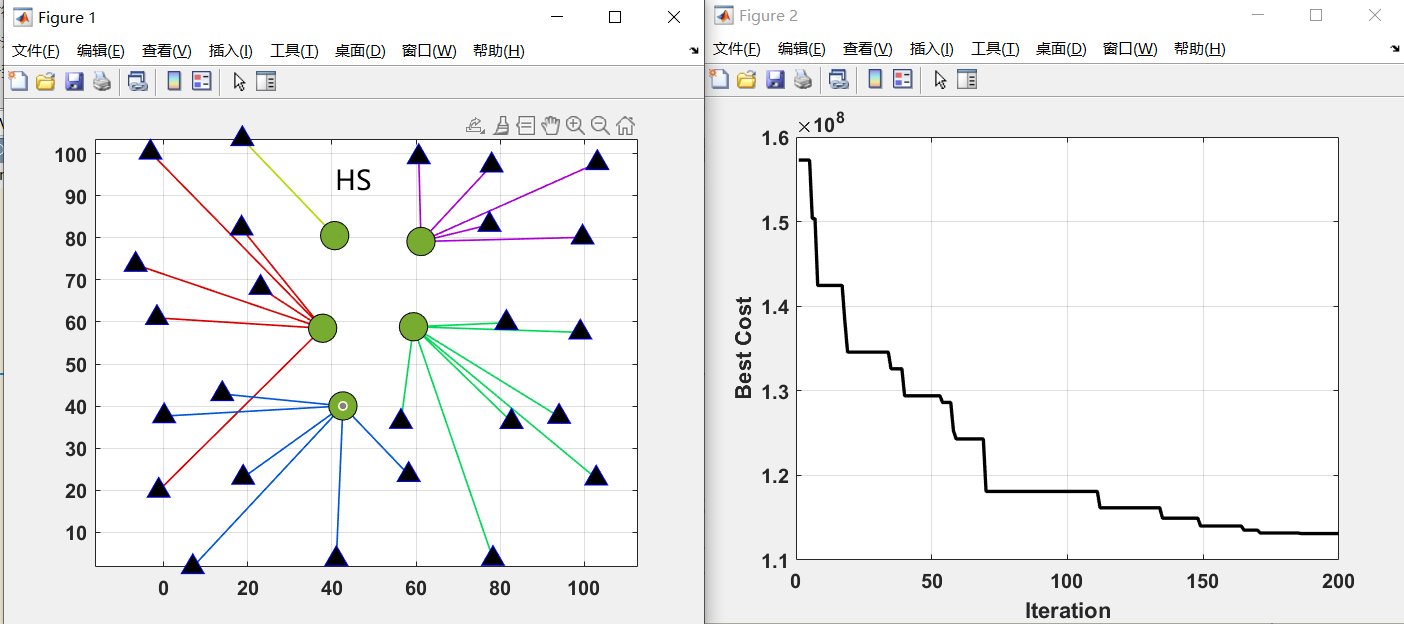
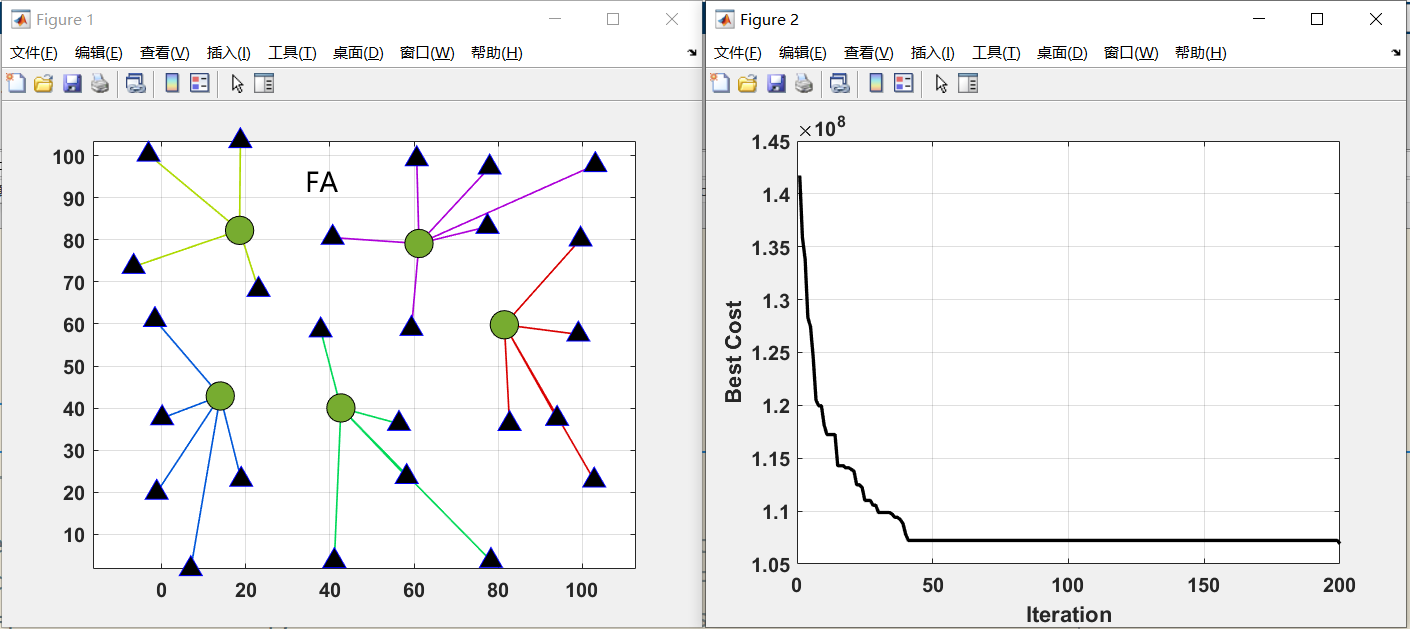
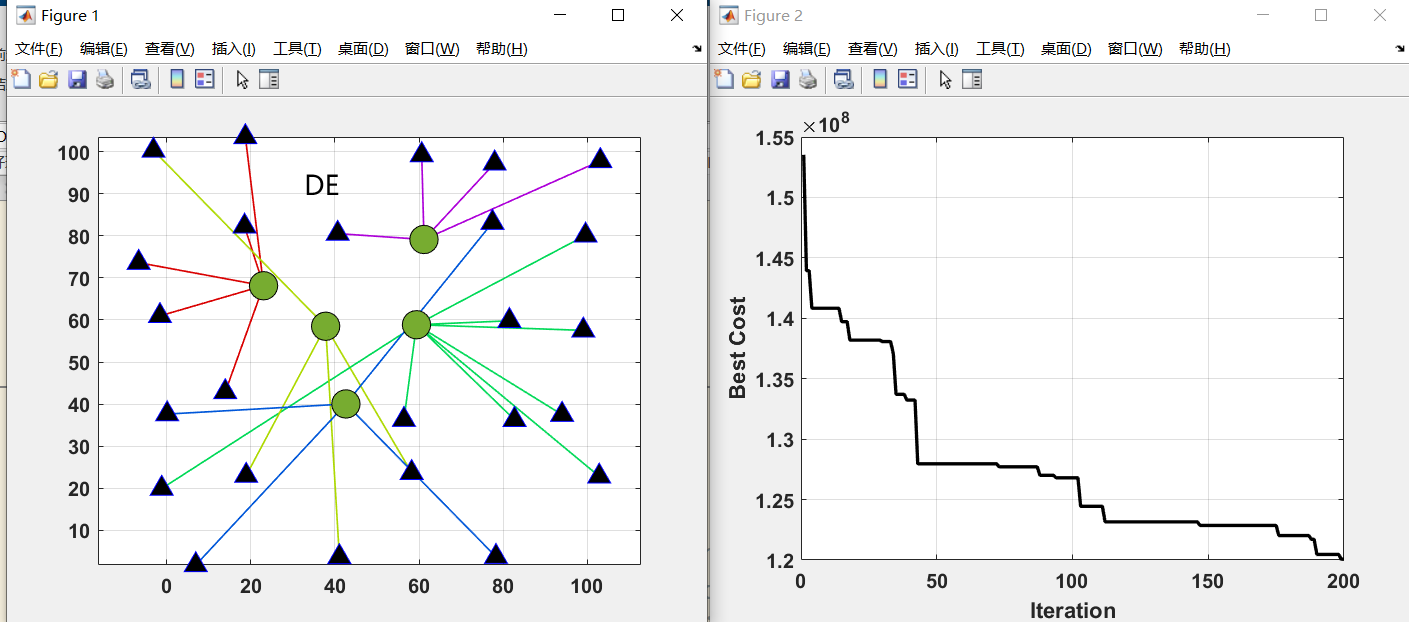
最后画一个三线表，比较一下目标函数和运行时间。
你用什么算法，什么算法就能达到最好。上面的图是我在matlab2022a运行的。可能不同版本也会有差距。原文中，作者就在不同性能的电脑上进行测试了。

写在最后

到此结束，感兴趣的去mathworks上下载源代码，原文。
mathworks用QQ邮箱可以免费注册，无需科学上网。

Seyed Muhammad Hossein Mousavi (2023). Victoria Amazonica Optimization VAO Algorithm (https://github.com/SeyedMuhammadHosseinMousavi/Victoria-Amazonica-Optimization-VAO-Algorithm), GitHub. 检索来源 2023/3/29.

本文由mdnice多平台发布