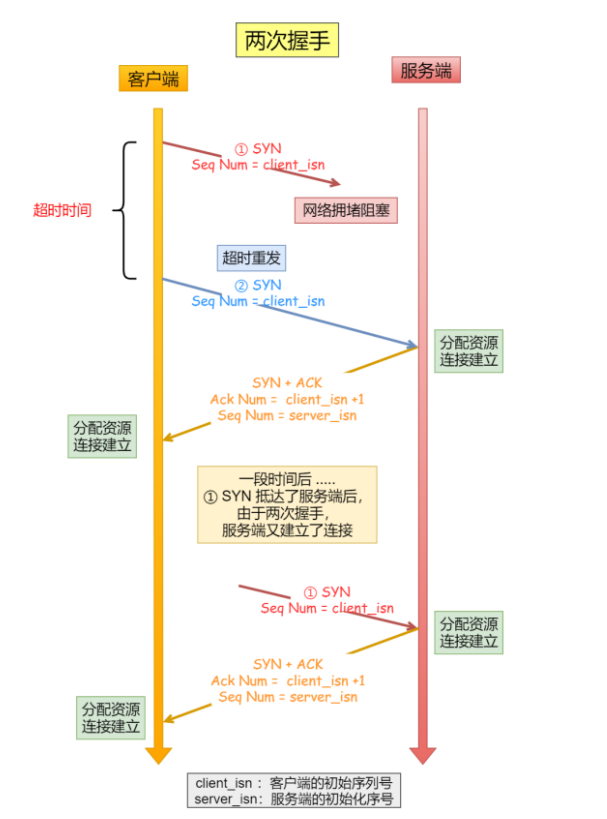
采用D-K迭代设计不确定对象的鲁棒控制器，将H∞综合(K步)与μ分析(D步)相结合，优化闭环鲁棒性能。

Step 1：利用H∞综合方法找到使标称系统闭环增益最小的控制器。

Step 2：进行鲁棒性分析，以估计闭环系统的鲁棒H∞性能。这个量表示为一个缩放的H∞范数，涉及动态缩放，称为D和G缩放(D步)。

Step 3：找到一个新的控制器来最小化在第2步(K步)中获得的缩放H∞范数。

Step 4：重复步骤2和3，直到鲁棒性能停止改善。

      设计目标是确定一个控制器K；同样对于所有的Δ∈Δ，max𝜔𝜎 [Δ（𝑗𝜔）]≤1maxωσ ̅  [Δ（jω）]≤1，闭环系统是稳定和满足的

μ 综合的目的是最小化结构化奇异值𝝁𝚫𝑷（.）μΔP（.）的峰值闭环传递函数矩阵FL（P，K）在所有稳定控制器K的集合上

D-K迭代设计是鲁棒控制中的一种方法，用于设计不确定对象的鲁棒控制器。该方法将H∞综合（K步）与μ分析（D步）相结合，通过迭代的方式不断调整控制器参数，以优化闭环鲁棒性能。

其中，μ综合是D-K迭代设计中的一个重要环节，用于通过结构化奇异值分析系统的鲁棒性能。μ综合的目标是最小化结构化奇异值的峰值，以提高系统的稳定性和鲁棒性能。

因此，μ综合是D-K迭代设计中不可或缺的一部分，能够有效地帮助设计出稳定、鲁棒的控制器。同时，μ综合也是鲁棒控制中的一种常用方法，可用于设计各种类型的鲁棒控制器，包括H∞控制器、μ合成控制器等。

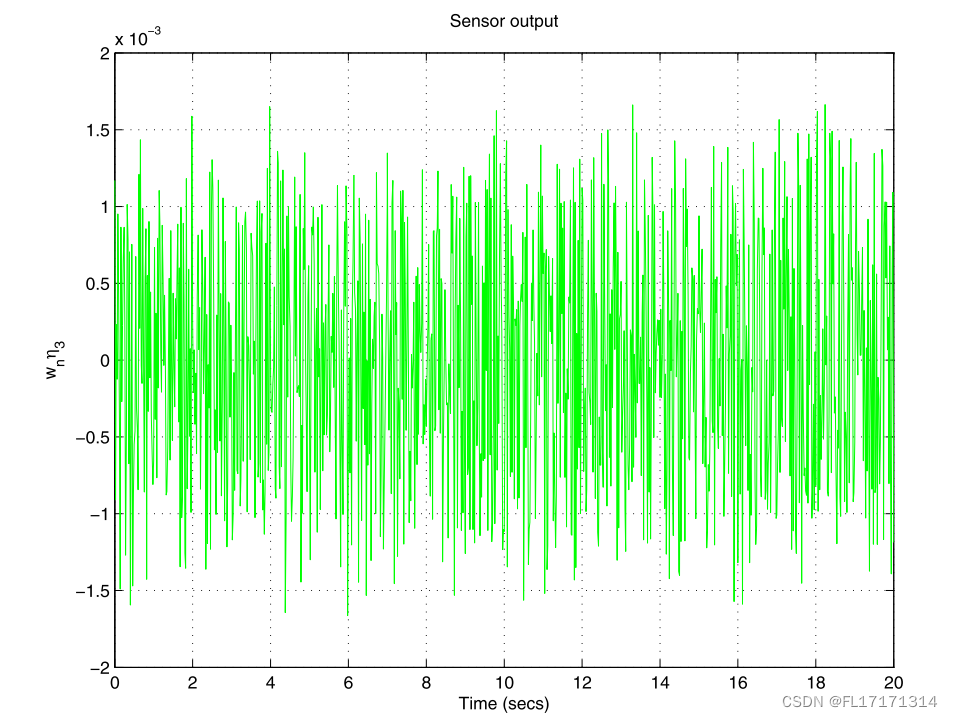
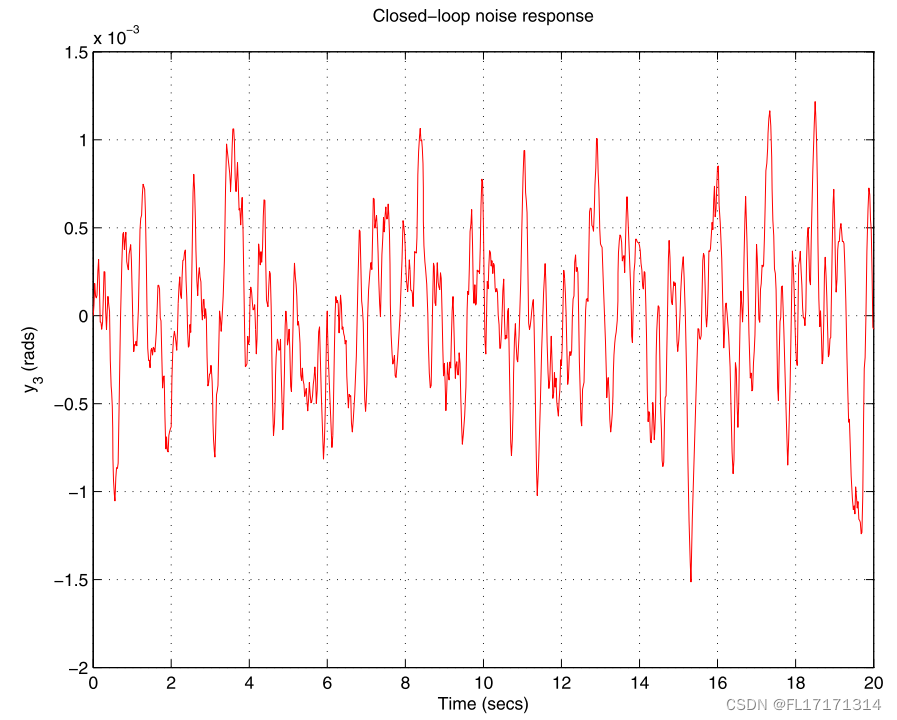
良好的干扰衰减需要足够大的闭环带宽。然而，这可能会导致在存在谐振模式的情况下实现鲁棒稳定性和鲁棒性能的困难。一些共振的频率远高于闭环带宽，因此看起来是无害的，甚至可能破坏系统的鲁棒稳定性。在这种情况下，有必要通过使用被动/主动阻尼技术来增加这些模式的阻尼。

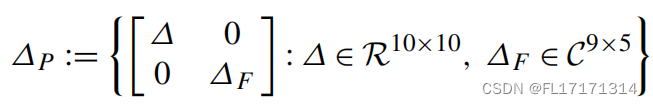
矩阵ΔP的第一个块，即不确定度块Δ，对应于被控系统中建模的参数和LTI不确定度。第二个块，ΔF，是一个虚构的不确定性块，引入了包括μ方法框架中的性能目标。这个块的输入是加权误差信号ey和eu，输出是外生输入r、d和η。 

————————————————————

控制器设计：

为了满足设计目标，需要找到一个稳定控制器K，使在每个频率ω∈[0，∞]下，结构奇异值μ满足该条件：

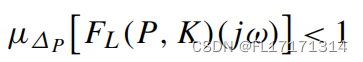
该条件的实现保证了闭环系统的鲁棒性性能，即：

 

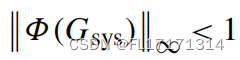
对于所有的稳定的扰动，Δ与Δ∞<1