1. 题目介绍（59. 队列的最大值）

面试题59：队列的最大值，一共分为两小题：

题目一：滑动窗口的最大值
题目二：队列的最大值

2. 题目1：滑动窗口的最大值

题目链接：https://leetcode.cn/problems/hua-dong-chuang-kou-de-zui-da-zhi-lcof/

2.1 题目介绍

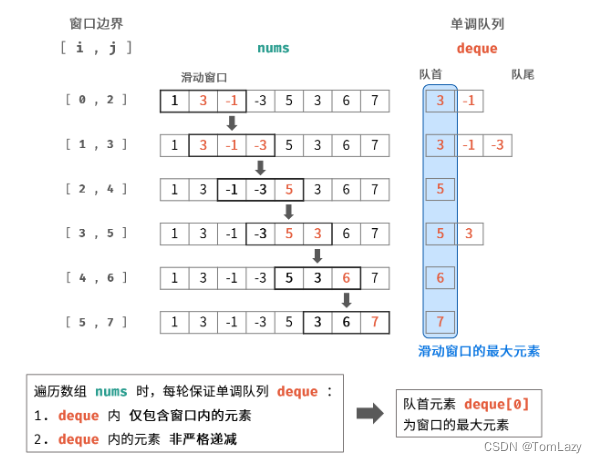
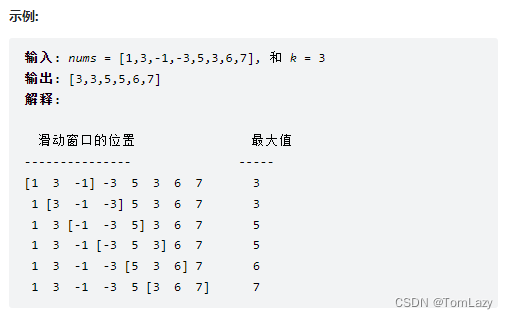
给定一个数组 nums 和滑动窗口的大小 k，请找出所有滑动窗口里的最大值。

【测试用例】：
在这里插入图片描述

【条件约束】：

提示：

你可以假设 k 总是有效的，在输入数组不为空的情况下，1 ≤ k ≤ nums.length。

【相关题目】：

注意：本题与主站 239. 滑动窗口最大值题目相同。

2.2 题解 – 单调队列 – O(n)

时间复杂度O(n)，空间复杂度O(k)

【解题思路】：
1. 蛮力法：扫描每个滑动窗口的所有数字并找出其中的最大值。

如果滑动窗口的大小为 k，则需要 O(k) 时间才能找出滑动窗口里的最大值。
对于长度为 n 的输入数组，这种算法的总时间复杂度是 O(nk)。

……
2. 单调队列：

我们可以通过双端队列来存储可能成为滑动窗口最大值的元素，且要保证队首元素始终为当前窗口的最大值：（主要有两步操作）

移除队首：即队首元素已经从窗口滑出
移除队尾：即队尾元素小于即将入队元素

……
将 “未形成窗口” 和 “形成窗口后” 两个阶段拆分到两个循环里实现，可以减少冗余的判断操作
……
【实现策略】：

首先进行无效输入判断，判断入参是否正确；
创建双端队列 deque 与返回数组 res；
将数组元素依次入队，并根据条件进行相应的移除操作，整个过程被分为了两个阶段：未形成窗口和形成窗口后；
在窗口移动的过程中，通过 res 存储当前窗口的最大值，并最终返回。

class Solution {
    // Solution1：双端队列
    public int[] maxSlidingWindow(int[] nums, int k) {
        // 无效输入判断
        if (nums.length <= 0 || k <= 0) return new int[0];
        // 创建双端队列
        Deque<Integer> deque = new LinkedList<>();
        // 定义数组变量，存储滑动窗口最大值
        int[] res = new int[nums.length - k + 1];
        // 未形成滑动窗口
        for (int i = 0; i < k; i++) {
            // 如果 队尾元素 小于 当前数组元素，就移除队尾
            while (!deque.isEmpty() && deque.peekLast() < nums[i])
                deque.removeLast();
            deque.addLast(nums[i]);
        }
        // 形成窗口后
        res[0] = deque.peekFirst();
        for(int i = k; i < nums.length; i++) {
            // 开始滑动窗口，队首已经从窗口移出
            if(deque.peekFirst() == nums[i - k])
                deque.removeFirst();
            // 如果 队尾元素 小于 当前数组元素，则移除队尾
            while(!deque.isEmpty() && deque.peekLast() < nums[i])
                deque.removeLast();
            deque.addLast(nums[i]);
            // 每滑动一次，记录一次当前窗口的最大值
            res[i - k + 1] = deque.peekFirst();
        }
        return res;
    }
}

在这里插入图片描述

3. 题目2：队列的最大值

题目链接：https://leetcode.cn/problems/dui-lie-de-zui-da-zhi-lcof/

3.1 题目介绍

请定义一个队列并实现函数 max_value 得到队列里的最大值，要求函数 max_value、push_back 和 pop_front 的均摊时间复杂度都是 O(1)。

若队列为空，pop_front 和 max_value 需要返回 -1

【测试用例】：
示例 1：

输入:
[“MaxQueue”,“push_back”,“push_back”,“max_value”,“pop_front”,“max_value”]
[[],[1],[2],[],[],[]]
输出: [null,null,null,2,1,2]

示例2：

输入:
[“MaxQueue”,“pop_front”,“max_value”]
[[],[],[]]
输出: [null,-1,-1]

【条件约束】：

限制：

1 <= push_back,pop_front,max_value的总操作数 <= 10000
1 <= value <= 10^5

3.2 题解 – 双端队列 – O(1)

时间复杂度O(1)，空间复杂度O(n)

【解题思路】：
1. 暴力求解：直接实现一个普通的队列，查询最大值时遍历计算；
2. 单调队列：该题解与上一题滑动窗口的最大值类似，具体过程可以参考上一题。

class MaxQueue {
    // 定义队列
    // queue 负责作为一个正常的队列结构
    // deque 用来存储当前队列的最大值
    Queue<Integer> queue;
    Deque<Integer> deque;

    // 初始化队列
    public MaxQueue() {
        queue = new LinkedList<>();
        deque = new LinkedList<>();
    }
    
    // 返回deque中的队首元素
    public int max_value() {
        return deque.isEmpty() ? -1 : deque.peekFirst();
    }
    
    // 从队尾方向入队
    public void push_back(int value) {
        // queue直接入队
        queue.offer(value);
        // deque需要判断一下该元素是否大于队尾元素，如果是则移除队尾
        while (!deque.isEmpty() && deque.peekLast() < value)
            deque.removeLast();
        deque.offerLast(value);
    }
    
    // 从队首方向出队
    public int pop_front() {
        // 判断当前是否队空
        if(queue.isEmpty()) return -1;
        // deque出不出队，取决于当前要出队的元素是不是最大值
        if (queue.peek().equals(deque.peekFirst())) deque.removeFirst();
        return queue.poll();
    }
}

/**
 * Your MaxQueue object will be instantiated and called as such:
 * MaxQueue obj = new MaxQueue();
 * int param_1 = obj.max_value();
 * obj.push_back(value);
 * int param_3 = obj.pop_front();
 */