1.背景

  推荐系统的两大应用场景分别是评分预测(Rating Prediction)和Top-N推荐(Item Ranking)。其中评分预测主要用于评价网站，比如用户给自己看过的电影评多少分，或者用户给自己看过的书籍评价多少分，矩阵分解技术主要应用于评分预测问题；Top-N推荐常用于购物网站或获取不到显式评分的网站，通过用户的隐式反馈为用户提供一个可能感兴趣的Item列表，此排序任务需要排序模型进行建模。本文主要介绍如何利用矩阵分解来解决评分预测问题。

2.矩阵分解概述

  协同过滤技术可划分为基于内存/邻域的协同过滤(Memory-based CF)与基于模型的协同过滤技术(Model-based CF)。这里基于模型的协同过滤技术中矩阵分解(Matrix Factorization，MF)技术最为普遍和流行，因为它的可扩展性好并且易于实现。

  矩阵分解是一种隐语义模型。隐语义模型是通过隐含特征(Latent Factor)联系用户兴趣和物品，基于用户行为的自动聚类。在评分预测问题中，收集到的用户行为评分数据可用一个评分矩阵表示，矩阵分解要做的是预测出评分矩阵中缺失的评分，使得预测评分能反映用户的喜欢程度，从而可以把预测评分最高的前K个电影推荐给用户。为了预测缺失的评分，矩阵分解学习 $User$ 矩阵和 $Item$ 矩阵，使得$User$矩阵$\ast$ $Item$矩阵​与评分矩阵中已知的评分差异最小，此时评分预测问题转化为了一个最优化问题，求解该最优化问题即可将评分矩阵分解成User矩阵和Item矩阵，从而可以计算出缺失的评分。

在评分预测问题中：

• 构建 user -item 评分矩阵(数据是稀疏的，矩阵分解就是填充缺失的评分)
• 学习 $User$ 矩阵和 $Item$ 矩阵，使得评分与矩阵中已知的评分差异最小(最优化问题)

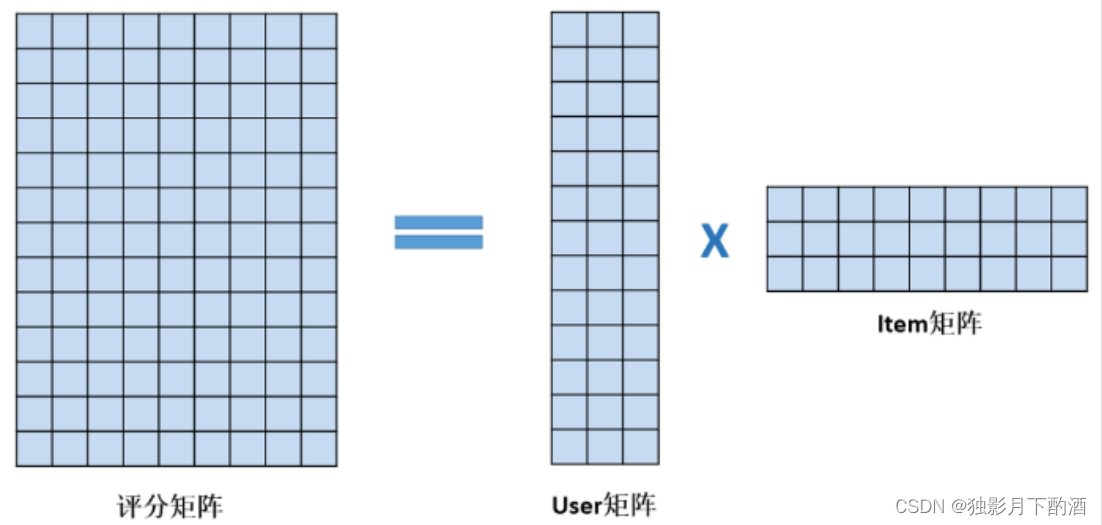
以电影评分预测为例，用评分矩阵表示收集到的用户行为数据，12个用户，9部电影。

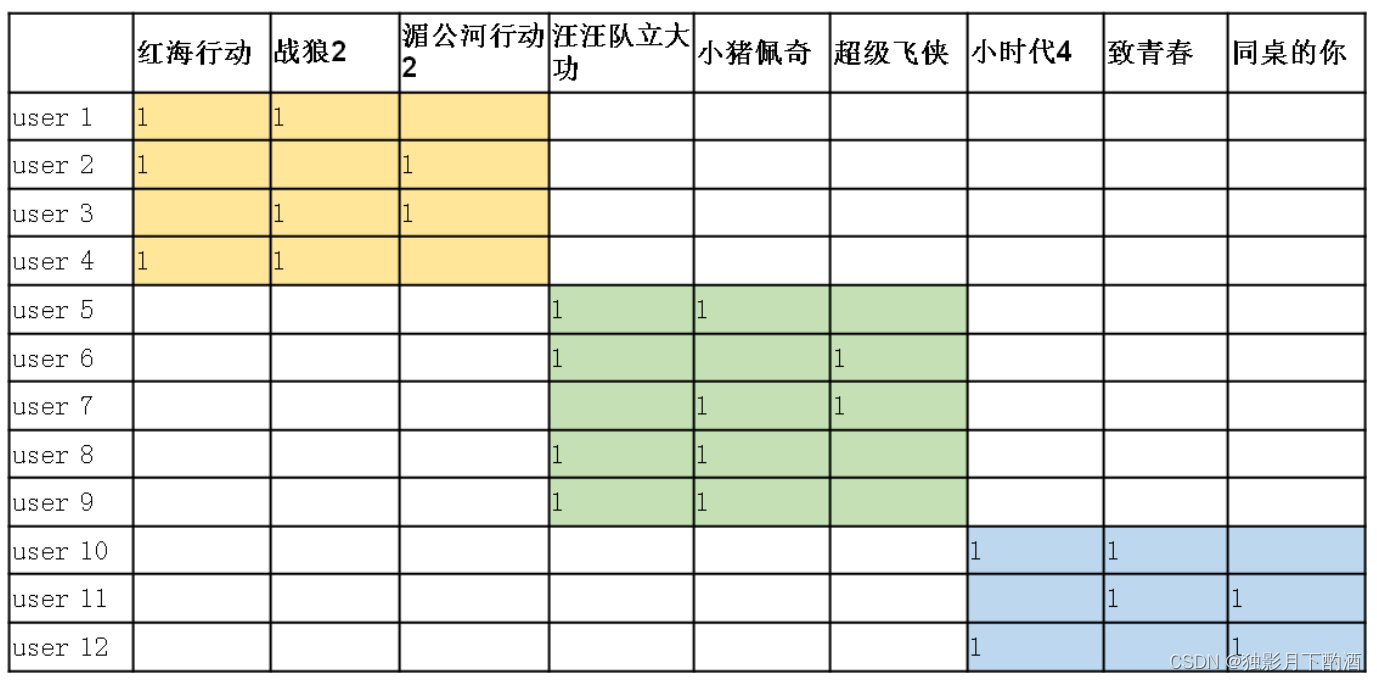
  对上述用户-物品评分矩阵(12×9)进行矩阵分解，得到User(12×3)矩阵和Item(3×9)矩阵。观察下图User矩阵，可知用户的观影爱好体现在User向量上，观察Item矩阵，可知电影的风格体现在Item向量上，MF用user向量和item向量的内积去拟合评分矩阵中该user对该item的评分，内积的大小反映了user对item的喜欢程度，内积越大表明用户对该电影的喜爱程度高，反之用户对该电影的喜爱程度低。这里“动作”、“动画”、“爱情”为隐含特征，隐含特征个数k越大，隐类别分得越细，计算量越大。

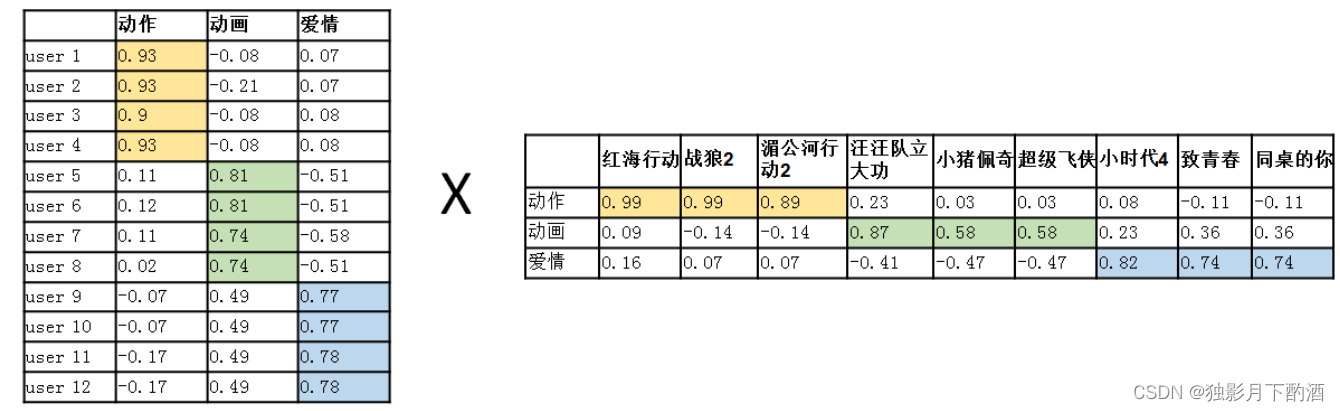
把User矩阵与Item矩阵相乘，就能预测每个用户对每部电影的预测评分了，评分值越大，表示用户喜欢该电影的可能性越大，该电影就越值得推荐给用户。

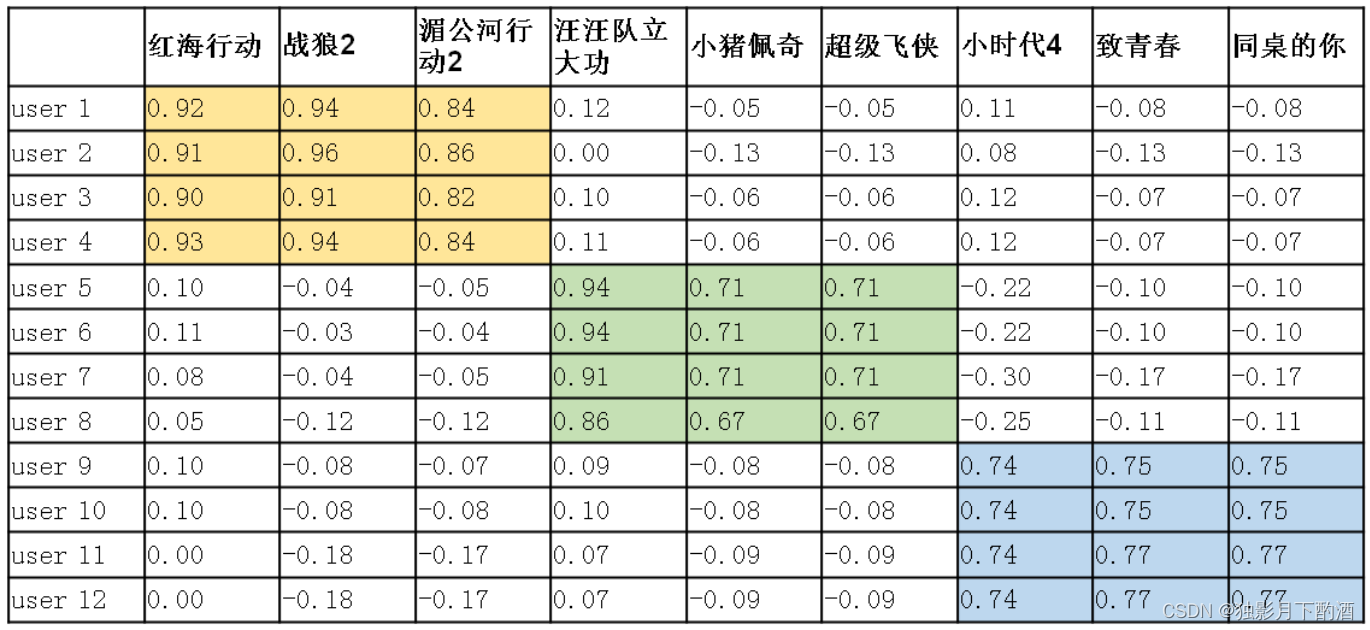
3.矩阵分解目标函数

在用户-物品评分矩阵 $\mathbf{R}$ 中，$r_{ui}$ 表示 用户 $u$ 对 Item $i$ 的评分 , 当 $r_{ui}>0$ 时，表示有评分，当$r_{ui}=0$，表示没有评分。

在User矩阵 $\mathbf{X}$ 中($M\times k$，用户数为M)，$x_u$ 表示用户 $u$ 的向量，k维列向量。$\mathbf{X}=[x_1,x_2,...,x_M]$

在Item矩阵 $\mathbf{Y}$ 中($k\times N$，物品数为N)，$y_i$ 表示用户 $ite{m}_i$ 的向量，k维列向量。$\mathbf{Y}=[y_1,y_2,...,y_N]$

用户向量与物品向量的内积，表示用户 $u$ 对物品 $i$ 的预测评分。矩阵分解的目标函数为：
$$\underset{X,Y}{\min }\sum _{r_{ui}\ne 0}{\left(r_{ui}-x_u^T{y}_i\right)}^2+\lambda \left(\sum _u||x_u|{|}_2^2+\sum _i||y_i|{|}_2^2\right)$$
上式前半部分表示的是User矩阵*Item矩阵与评分矩阵中已知的评分差异，后半部分是L2正则项，保证数值计算稳定性，防止过拟合。

4.目标函数最优化问题求解

  目标函数最优化问题的工程解法一般采用交替最小二乘法( Alternating Least Squares , ALS)或随机梯度下降(SGD)。 在实际应用中，交替最小二乘更常用一些，这也是社交巨头 Facebook 在他们的推荐系统中选择的主要矩阵分解方法。

4.1 交替最小二乘法(ALS)

交替最小二乘的核心是 “交替”，接下来看看 ALS 是如何 “交替” :

矩阵分解的最终任务是找到两个矩阵 $\mathbf{X}$ 和 $\mathbf{Y}$，让它们相乘后约等于原矩阵 $\mathbf{R}$：
$${\mathbf{R}}_{m\times n}={\mathbf{X}}_{m\times k}\times {\mathbf{Y}}_{n\times k}^T$$
难就难在，$\mathbf{X}$ 和$\mathbf{Y}$ 两个都是未知的，如果知道其中一个的话，就可以按照线性代数标准解法求得，比如如果知道了 $\mathbf{Y}$，那么 $\mathbf{X}$ 就可以这样算：
$${\mathbf{R}}_{m\times n}={\mathbf{X}}_{m\times k}\times {\mathbf{Y}}_{n\times k}^{-1}$$
也就是 $\mathbf{R}$ 矩阵乘以 $\mathbf{Y}$ 矩阵的逆矩阵就得到了结果，反之知道了 $\mathbf{X}$ 再求$\mathbf{Y}$ 也是一样。

交替最小二乘通过迭代的方式解决了这个鸡生蛋蛋生鸡的难题：

1. 初始化随机矩阵 $\mathbf{Y}$ 里面的元素值；
2. 把 $\mathbf{Y}$ 矩阵当做已知的，直接用线性代数的方法求得矩阵 $\mathbf{X}$；
3. 得到了矩阵 $\mathbf{X}$后，把 $\mathbf{X}$ 当做已知的，故技重施，回去求解矩阵 $\mathbf{Y}$ ；
4. 上面两个过程交替进行，一直到误差满足设定条件为止。

交替最小二乘法步骤：

• $\mathbf{S}tep1$，固定 $\mathbf{Y}$ 优化 $\mathbf{X}$
  $$\underset{X}{\min }\sum _{r_{ui}\ne 0}{\left(r_{ui}-x_u^T{y}_i\right)}^2+\lambda \sum _u||x_u|{|}_2^2$$
  将目标函数转化为矩阵表达形式：
  $$J(x_u)=(R_u-Y_u^T{x}_u{)}^T(R_u-Y_u^T{x}_u)+\lambda x_u^T{x}_u$$
  其中 $R_u=[r_{u{i}_1},r_{u{i}_2},...r_{u{i}_n}{]}^T$ 表示用户 $u$ 对 $n$ 个物品的评分；$Y_u=[y_{i_1},y_{i_2},...y_{i_m}]$ 为 $n$ 个物品的向量。

  求解目标函数 $J$ 关于 $x_u$ 的梯度，并令梯度等于0，得到：
  $$\frac{\partial J(x_u)}{\partial x_u}=-2Y_u(R_u-Y_u^T{x}_u)+2\lambda x_u=0$$
  求解后可得：
  $$x_u=(Y_u{Y}_u^T+\lambda I{)}^{-1}{Y}_u{R}_u$$

• $\mathbf{S}tep2$，固定 $\mathbf{X}$ 优化 $\mathbf{Y}$
  $$\underset{Y}{\min }\sum _{r_{ui}\ne 0}{\left(r_{ui}-x_u^T{y}_i\right)}^2+\lambda \sum _i||y_i|{|}_2^2$$

  • 将目标函数转化为矩阵表达形式：
    $$J(y_i)=(R_i-X_i^T{y}_i{)}^T(R_i-X_i^T{y}_i)+\lambda y_i^T{y}_i$$
    其中$R_u=[r_{u_{1}i},r_{u_{2}i},...r_{u_{m}i}{]}^T$表示 $m$个用户对个物品 $i$ 的评分；$X_i=[x_{u_1},x_{u_2},...x_{u_m}]$ 为 $m$个用户的向量。

    求解目标函数 $J$关于 $y_i$ 的梯度，并令梯度等于0，得到：
    $$\frac{\partial J(y_i)}{\partial x_i}=-2X_i(R_i-X_i^T{y}_i)+2\lambda y_i=0$$
    求解后可得：
    $$y_i=(X_i{X}_i^T+\lambda I{)}^{-1}{X}_i{R}_i$$

• 重复$\mathbf{S}tep1$和$2$，直到 $\mathbf{X}$ 和 $\mathbf{Y}$ 收敛，每次固定一个矩阵，优化另一个矩阵，都是最小二乘问题

  除了针对显式评分矩阵，ALS还可以对隐式矩阵进行分解，将评分看成行为的强度，比如浏览次数，阅读时间等。 当 $r_{ui}>0$时， 表示用户 $u$对商品 $i$ 有行为，当 $r_{ui}=0$， 表示用户 $u$对商品 $i$ 没有行为。
$$P_{ui}=\{\begin{array}{ll}1& r_{ui}>0\\ 0& r_{ui}=0\end{array}$$
上式 $P_{ui}$ 称为用户偏好：当用户$u$对物品$i$有过行为，认为用户$u$对物品$i$感兴趣，$P_{ui}$=1；当用户$u$对物品$i$没有过行为，认为用户$u$对物品$i$不感兴趣，$P_{ui}$=0.

对隐式矩阵进行分解的步骤:

• 引入置信度($\alpha$ 为置信系数)
  $$c_{ui}=1+\alpha r_{ui}$$
  当$r_{ui}>0$时， $c_{ui}$ 与 $r_{ui}$ 线性递增，当 $r_{ui}=0$时， $c_{ui}=1$，即 $c_{ui}$ 最小值为1.

• 目标函数
  $$\underset{X,Y}{\min }\sum _{u=1}^m\sum _{i=1}^n{c}_{ui}{\left(r_{ui}-x_u^T{y}_i\right)}^2+\lambda \left(\sum _u||x_u|{|}_2^2+\sum _i||y_i|{|}_2^2\right)$$

• ALS求解矩阵$\mathbf{X}$和$\mathbf{Y}$

ALS工具

• spark ml库（官方推荐）
• python代码：https://github.com/tushushu/imylu/blob/master/imylu/recommend/als.py

4.2 随机梯度下降SGD

  SGD基本思路是以随机方式遍历训练集中的数据，并给出每个已知评分的预测评分。用户和物品特征向量的调整就沿着评分误差越来越小的方向迭代进行，直到误差达到要求。所以，SGD不需要遍历所有的样本即可完成特征向量的求解。

矩阵分解的目标函数为：
$$J(x_u,y_i)=\underset{X,Y}{\min }\sum _{r_{ui}\ne 0}{\left(r_{ui}-x_u^T{y}_i\right)}^2+\lambda \left(\sum _u||x_u|{|}_2^2+\sum _i||y_i|{|}_2^2\right)$$
分别求解$J(x_u,y_i)$关于 $x_u$ 和 $y_i$的梯度如下：
$$\begin{array}{rl}& \frac{\partial J(x_u,y_i)}{\partial x_u}=\sum _{u,r_{ui}\ne 0}-2\left(r_{ui}-x_u^T{y}_i\right)y_i+\sum _{u}2\lambda ||x_u|{|}_2\\ & \frac{\partial J(x_u,y_i)}{\partial y_i}=\sum _{i,r_{ui}\ne 0}-2\left(r_{ui}-x_u^T{y}_i\right)x_u+\sum _{i}2\lambda ||y_i|{|}_2\end{array}$$
不断更新矩阵 $\mathbf{X}$ 和 $\mathbf{Y}$
$$\begin{array}{rl}& x_u=x_u+\alpha (\sum _{u,r_{ui}\ne 0}-2\left(r_{ui}-x_u^T{y}_i\right)y_i+\sum _{u}2{\lambda }_1||x_u|{|}_2)\\ & y_i=y_i+\alpha (\sum _{i,r_{ui}\ne 0}-2\left(r_{ui}-x_u^T{y}_i\right)x_u+\sum _{i}2{\lambda }_2||y_i|{|}_2)\end{array}$$
由于 $\mathbf{X}$ 和 $\mathbf{Y}$ 是两个不同的矩阵，通常分别采取不同的正则参数，如 ${\lambda }_1$和${\lambda }_2$

5.矩阵分解算法

  MF(Matrix Factorization，矩阵分解)模型核心思想是通过两个低维小矩阵(一个代表用户embedding矩阵，一个代表物品embedding矩阵)的乘积计算，来模拟真实用户点击或评分产生的大的协同信息稀疏矩阵，本质上是编码了用户和物品协同信息的降维模型。

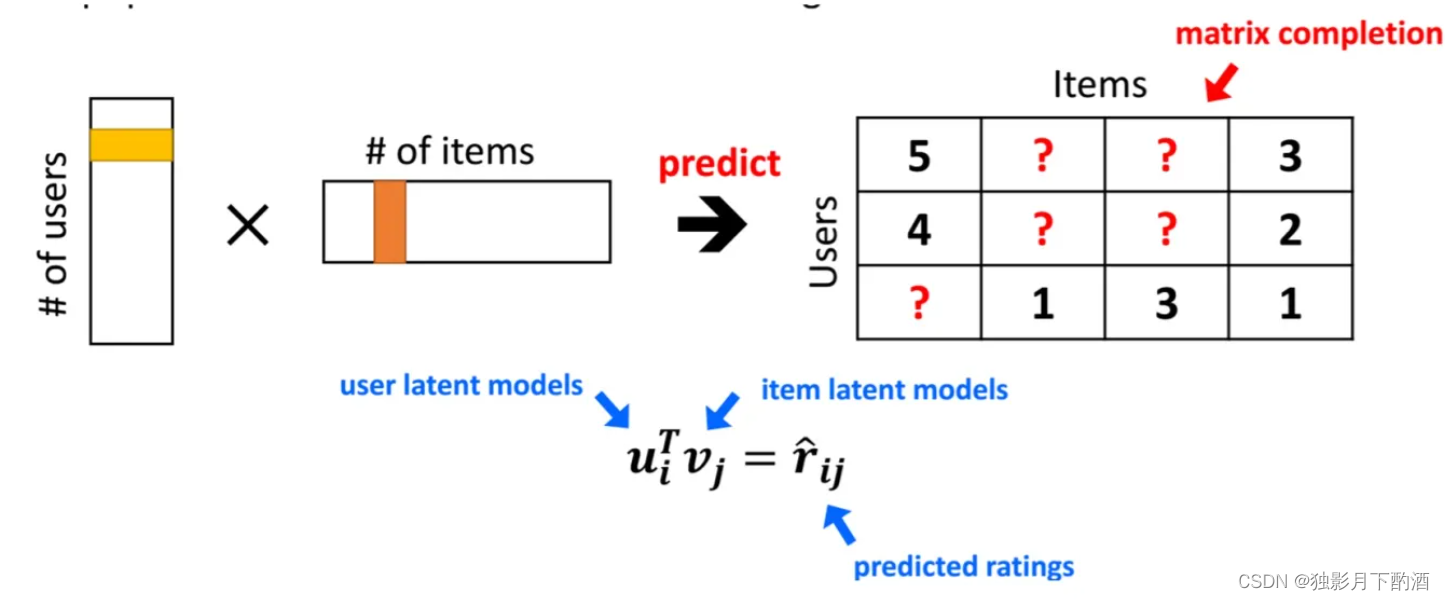
当训练完成，每个用户和物品得到对应的低维embedding表达后，如果要预测某个 $Use{r}_i$ 对 $Ite{m}_j$ 的评分的时候，只要它们做个内积计算 $<Use{r}_i,Ite{m}_j>$ ，这个得分就是预测得分。

5.1 Traditional SVD

5.1.1 回顾特征值和特征向量

特征值和特征向量的定义如下：
$$Ax=\lambda x$$
其中 $A$ 是一个 $n\times n$ 的实对称矩阵，$x$ 是一个 $n$ 维向量，则我们说 $\lambda$ 是矩阵 $A$ 的一个特征值，而 $x$ 是矩阵 $A$ 的特征值 $\lambda$ 所对应的特征向量。

求出特征值和特征向量有什么好处呢?

可以将矩阵A特征分解。

如果我们求出了矩阵$A$的$n$个特征值${\lambda }_1\le {\lambda }_2\le ...\le {\lambda }_n$,以及这 $n$个特征值所对应的特征向量$w_1,w_2,...w_n$，如果这 $n$ 个特征向量线性无关，那么矩阵 $A$ 就可以用下式的特征分解表示：
$$A=W\Sigma W^{-1}$$
其中 $W$ 是这 $n$ 个特征向量所张成的 $n\times n$ 维矩阵，而 $\Sigma$ 为这 $n$ 个特征值为主对角线的 $n\times n$ 维矩阵。

一般我们会把$W$的这$n$个特征向量标准化，即满足$||w_i|{|}_2=1$, 或者说 $w_i^T{w}_i=1$，此时 $W$ 的 $n$ 个特征向量为标准正交基，满足$W^{T}W=I$，即$W^T=W^{-1}$, 也就是说$W$为酉矩阵。
$$A=W\Sigma W^T$$
注意到要进行特征分解，矩阵$A$必须为方阵。那么如果$A$不是方阵，即行和列不相同时，我们还可以对矩阵进行分解吗？答案是可以，此时我们的SVD登场了。

5.1.2 SVD

假设矩阵$A$是一个$m\times n$的矩阵，那么我们定义矩阵$A$的SVD为： ：
$$A=U\Sigma V^T$$
其中 $U$ 是一个 $m\times m$ 的矩阵，$\Sigma$ 是一个 $m\times n$ 的矩阵，除了主对角线上的元素以外全为 $0$ ，主对角线上的每个元素都称为奇异值，$V$是一个 $n\times n$ 的矩阵。$U$ 和 $V$ 都是酉矩阵，即满足$U^{T}U=I,V^{T}V=I$。下图可以很形象的看出上面SVD的定义：

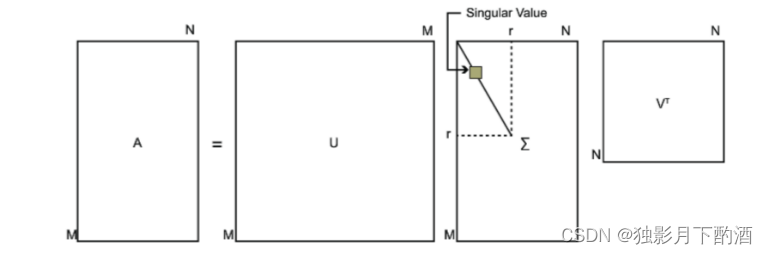
如何求出SVD分解后的$U,\Sigma ,V$这三个矩阵呢？

如果将$A$的转置和$A$做矩阵乘法，那么会得到$n\times n$的一个方阵$A^{T}A$。既然$A^{T}A$是方阵，那么可以进行特征分解，得到的特征值和特征向量满足下式：
$$(A^{T}A)v_i={\lambda }_i{v}_i$$
这样可以得到矩阵$A^{T}A$的$n$个特征值和对应的$n$个特征向量$v$了。将$A^{T}A$的所有特征向量张成一个$n\times n$的矩阵$V$，即为SVD公式里面的$V$矩阵了。一般将$V$中的每个特征向量叫做$A$的右奇异向量。

如果我们将A和A的转置做矩阵乘法，那么会得到$m\times m$的一个方阵$A{A}^T$。既然$A{A}^T$是方阵，那么可以进行特征分解，得到的特征值和特征向量满足下式：
$$(A{A}^T)u_i={\lambda }_i{u}_i$$
这样可以得到矩阵$A{A}^T$的$n$个特征值和对应的$m$个特征向量$u$了。将$A{A}^T$的所有特征向量张成一个$m\times m$的矩阵$U$，即为SVD公式里面的$U$矩阵了。一般将$U$中的每个特征向量叫做$A$的左奇异向量。

$U$和$V$都求出来了，现在就剩下奇异值矩阵 $\Sigma$ 没有求出了。由于除了对 $\Sigma$ 角线上是奇异值其他位置都是0，那只需要求出每个奇异值$\sigma$ 就可以了。
$$A=U\Sigma V^T\Rightarrow AV=U\Sigma V^{T}V\Rightarrow AV=U\Sigma \Rightarrow A{v}_i={\sigma }_i{u}_i\Rightarrow {\sigma }_i=A{v}_i/u_i$$
这样我们可以求出我们的每个奇异值，进而求出奇异值矩阵$\Sigma$。

$A^{T}A$的特征向量组成的就是我们SVD中的$V$矩阵，而$A{A}^T$的特征向量组成的就是我们SVD中的$U$矩阵，这有什么根据吗？这个其实很容易证明，我们以$V$矩阵的证明为例。
$$A=U\Sigma V^T\Rightarrow A^T=V{\Sigma }^T{U}^T\Rightarrow A^{T}A=V{\Sigma }^T{U}^{T}U\Sigma V^T=V{\Sigma }^2{V}^T$$
上式证明使用了: $U^{T}U=I,{\Sigma }^T\Sigma ={\Sigma }^2$。 可以看出$A^{T}A$的特征向量组成的的确就是我们SVD中的$V$矩阵。类似的方法可以得到$A{A}^T$的特征向量组成的就是我们SVD中的$U$矩阵。

特征值矩阵等于奇异值矩阵的平方，也就是说特征值和奇异值满足如下关系：
$${\sigma }_i=\sqrt{{\lambda }_i}$$
通过求出$A^{T}A$的特征值取平方根来求奇异值更加方便。

5.1.3 SVD的性质

  对于奇异值,它跟特征分解中的特征值类似，在奇异值矩阵中也是按照从大到小排列，而且奇异值的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。也就是说，可以用最大的$k$个的奇异值和对应的左右奇异向量来近似描述矩阵。也就是说：
$$A_{m\times n}=U_{m\times m}{\Sigma }_{m\times n}{V}_{n\times n}^T\approx U_{m\times k}{\Sigma }_{k\times k}{V}_{k\times n}^T$$
  SVD可以用于PCA降维，来做数据压缩和去噪。也可以用于推荐算法，将用户和喜好对应的矩阵做特征分解，进而得到隐含的用户需求来做推荐。同时也可以用于NLP中的算法，比如潜在语义索引(LSI)。

5.1.4 SVD与PCA的关系

PCA的算法流程

求样本$x^{(i)}$的$n^{\prime }$维的主成分其实就是求样本集的协方差矩阵$X{X}^T$的前$n^{\prime }$个特征值对应特征向量矩阵$W$，然后对于每个样本$x^{(i)}$，做如下变换 $z^{(i)}=W^T{x}^{(i)}$，即达到降维的PCA目的。

下面我们看看具体的算法流程。

输入：$n$维样本集$D=(x^{(1)},x^{(2)},...,x^{(m)})$，要降维到的维数$n^{\prime }$.

输出：降维后的样本集$D\prime$

1. 对所有的样本进行中心化： $x^{(i)}=x^{(i)}-\frac{1}{m}\sum _{j=1}^m{x}^{(j)}$

2. 计算样本的协方差矩阵$X{X}^T$

3. 对矩阵$X{X}^T$进行特征值分解

4）取出最大的n’个特征值对应的特征向量$(w_1,w_2,...,w_n\prime )$, 将所有的特征向量标准化后，组成特征向量矩阵$W$。

5）对样本集中的每一个样本$x^{(i)}$,转化为新的样本$z^{(i)}=W^T{x}^{(i)}$

6. 得到输出样本集$D^{\prime }=(z^{(1)},z^{(2)},...,z^{(m)})$

有时候，我们不指定降维后的$n^{\prime }$的值，而是换种方式，指定一个降维到的主成分比重阈值$t$。这个阈值$t$在$(0,1]$之间。假如我们的n个特征值为${\lambda }_1\ge {\lambda }_2\ge ...\ge {\lambda }_n$,则$n^{\prime }$可以通过下式得到:
$$\frac{\sum _{i=1}^{n^{\prime }}{\lambda }_i}{\sum _{i=1}^n{\lambda }_i}\ge t$$
SVD用于PCA

PCA仅仅使用了我们SVD的右奇异矩阵，没有使用左奇异矩阵，那么左奇异矩阵有什么用呢？

现有样本是$m\times n$的矩阵$X$，如果我们通过SVD找到了矩阵$X{X}^T$最大的$d$个特征向量张成的$m\times d$维矩阵$U$，则如果进行如下处理：
$$X_{d\times n}^{\prime }=U_{d\times m}^T{X}_{m\times n}$$
可得一个$d\times n$的矩阵$X＇$，和原来的$m\times n$维样本矩阵$X$相比，行数从$m$减到了$d$，可见对行数进行了压缩。也就是说，左奇异矩阵可以用于行数的压缩。相对的，右奇异矩阵可以用于列数即特征维度的压缩，也就是PCA降维。

5.2 FunkSVD(LFM)

  2006年的Netflix Prize之后， Simon Funk公布了一个矩阵分解算法叫做Funk-SVD, 后来被 Netflix Prize 的冠军Koren称为Latent Factor Model(LFM)。

  FunkSVD是在传统SVD面临计算效率问题时提出来的，既然将一个矩阵做SVD分解成3个矩阵很耗时，同时还面临稀疏的问题，那么能不能避开稀疏问题的同时只分解成两个矩阵呢？即现在期望我们的矩阵$M$这样进行分解：
$$M_{m\times n}=P_{m\times k}^T{Q}_{k\times n}$$

目标:让用户的评分和用矩阵乘积得到的评分残差尽可能的小，也就是说，可以用均方差作为损失函数，来寻找最终的$P$和$Q$。

  对于某一个用户评分$m_{ij}$，如果用FunkSVD进行矩阵分解，则对应的表示为$q_j^T{p}_i$，采用均方差做为损失函数，则我们期望$(m_{ij}-q_j^T{p}_i{)}^2$尽可能的小，如果考虑所有的物品和样本的组合，则我们期望最小化下式：
$$\sum _{i,j}(m_{ij}-q_j^T{p}_i{)}^2$$
只要能最小化上面的式子，并求出极值所对应的$p_i,q_j$，则可以得到矩阵$P$和$Q$，那么对于任意矩阵$M$任意一个空白评分的位置，我们可以通过$q_j^T{p}_i$计算预测评分。

在实际应用中，为了防止过拟合，会加入一个L2的正则化项，因此正式的FunkSVD的优化目标函数$J(p,q)$是这样的：
$$\underset{p_i,q_j}{\underbrace{argmin}}\sum _{i,j}(m_{ij}-q_j^T{p}_i{)}^2+\lambda (||p_i|{|}_2^2+||q_j|{|}_2^2)$$
其中 $\lambda$ 为正则化系数，需要调参。对于这个优化问题，一般通过梯度下降法来进行优化得到结果。

将上式分别对$p_i,q_j$求导得:
$$\begin{array}{rl}& \frac{\partial J}{\partial p_i}=-2(m_{ij}-q_j^T{p}_i)q_j+2\lambda p_i\\ & \frac{\partial J}{\partial q_j}=-2(m_{ij}-q_j^T{p}_i)p_i+2\lambda q_j\end{array}$$
则在梯度下降法迭代时，$p_i,q_j$的迭代公式为：
$$\begin{array}{rl}& p_i=p_i+\alpha ((m_{ij}-q_j^T{p}_i)q_j-\lambda p_i)\\ & q_j=q_j+\alpha ((m_{ij}-q_j^T{p}_i)p_i-\lambda q_j)\end{array}$$
通过迭代我们最终可以得到$P$和$Q$，进而用于推荐。

5.3 BiasSVD算法

BiasSVD算法是在FunkSVD算法的基础上考虑了用户和商品的偏好。用户有自己的偏好(Bias)，比如乐观的用户打分偏高；商品也有自己的偏好(Bias)，比如质量好的商品，打分偏高；BiasSVD算法将与个性化无关的部分，设置为偏好(Bias)部分。

假设评分系统平均分为 $\mu$，第i个用户的用户偏置项为 $b_i$ ,而第 $j$ 个物品的物品偏置项为 $b_j$，则加入了偏置项以后的优化目标函数 $J(p,q)$ 如下：
$$\underset{p_i,q_j}{\underbrace{argmin}}\sum _{i,j}(m_{ij}-\mu -b_i-b_j-q_j^T{p}_i{)}^2+\lambda (||p_i|{|}_2^2+||q_j|{|}_2^2+||b_i|{|}_2^2+||b_j|{|}_2^2)$$
优化目标也可以采用梯度下降法求解。 $b_i,b_j$一般可以初始设置为$0$，然后参与迭代。$b_i,b_j$迭代方法如下：
$$\begin{array}{rl}& b_i=b_i+\alpha (m_{ij}-\mu -b_i-b_j-q_j^T{p}_i-\lambda b_i)\\ & b_j=b_j+\alpha (m_{ij}-\mu -b_i-b_j-q_j^T{p}_i-\lambda b_j)\end{array}$$
通过迭代我们最终可以得到$P$和$Q$，进而用于推荐。

5.4 SVD++算法

SVD++算法在BiasSVD算法上进一步做了增强，这里它增加考虑用户的隐式反馈。

对于某一个用户$i$，它提供了隐式反馈的物品集合定义为$N(i)$, 这个用户对某个物品$j$对应的隐式反馈修正的评分值为$c_{ij}$, 那么该用户所有的评分修正值为$\sum _{s\in N(i)}{c}_{is}$。一般我们将它表示为用$q_s^T{y}_i$形式，则加入了隐式反馈项以后的优化目标函数$J(p,q)$如下:
$$\underset{p_i,q_j}{\underbrace{argmin}}\sum _{i,j}(m_{ij}-\mu -b_i-b_j-q_j^T{p}_i-q_j^T|N(i){|}^{-1/2}\sum _{s\in N(i)}{q}_s{)}^2+\lambda (||p_i|{|}_2^2+||q_j|{|}_2^2+||b_i|{|}_2^2+||b_j|{|}_2^2+\sum _{s\in N(i)}||q_s|{|}_2^2)$$
其中，引入$|N(i){|}^{-1/2}$是为了消除不同$|N(i)|$个数引起的差异。式子够长的，不过需要考虑用户的隐式反馈时，使用SVD++还是不错的选择。

6.矩阵分解算法的优缺点

优点：

1. 泛化能力强。一定程度上解决了数据稀疏的问题。

2. 空间复杂度低。 仅仅存储用户和物品隐向量。空间复杂度有 $n^2$ 降低到 $(m+n)\ast k$

3. 更好的扩展性和灵活性。 矩阵分解的最终产物是用户和物品隐向量， 这个深度学习的embedding思想不谋而合， 因此矩阵分解的结果非常便于与其他特征进行组合和拼接， 并可以与深度学习无缝结合。

缺点：

1. 矩阵分解算法依然是只用到了评分矩阵， 没有考虑到用户特征， 物品特征和上下文特征， 这使得矩阵分解丧失了利用很多有效信息的机会。
2. 在缺乏用户历史行为的时候， 无法进行有效的推荐。

本文仅仅做个人学习记录所用，不作为商业用途，谢谢理解。

参考：

1.https://www.cnblogs.com/pinard/p/6351319.html

2.https://alice1214.github.io/%E6%8E%A8%E8%8D%90%E7%AE%97%E6%B3%95/2020/07/08/%E6%8E%A8%E8%8D%90%E7%AE%97%E6%B3%95%E5%AD%A6%E4%B9%A0-%E4%BA%94-%E7%9F%A9%E9%98%B5%E5%88%86%E8%A7%A3/