LeetCode算法小抄--快速排序详解及应用
- 快速排序详解及应用
- 代码实现
- 快速选择算法(Quick Select)-- 变体
- [215. 数组中的第K个最大元素](https://leetcode.cn/problems/kth-largest-element-in-an-array/)
- [剑指 Offer II 076. 数组中的第 k 大的数字](https://leetcode.cn/problems/xx4gT2/)
⚠申明: 未经许可,禁止以任何形式转载,若要引用,请标注链接地址。 全文共计9208字,阅读大概需要5分钟
🌈更多学习内容, 欢迎👏关注👀【文末】我的个人微信公众号:不懂开发的程序猿
个人网站:https://jerry-jy.co/
快速排序详解及应用
框架
void sort(int[] nums, int lo, int hi) {
if (lo >= hi) {
return;
}
// 对 nums[lo..hi] 进行切分
// 使得 nums[lo..p-1] <= nums[p] < nums[p+1..hi]
int p = partition(nums, lo, hi);
// 去左右子数组进行切分
sort(nums, lo, p - 1);
sort(nums, p + 1, hi);
}
对比二叉树的前序遍历
/* 二叉树遍历框架 */
void traverse(TreeNode root) {
if (root == null) {
return;
}
/****** 前序位置 ******/
print(root.val);
/*********************/
traverse(root.left);
traverse(root.right);
}
快速排序是先将一个元素排好序,然后再将剩下的元素排好序。
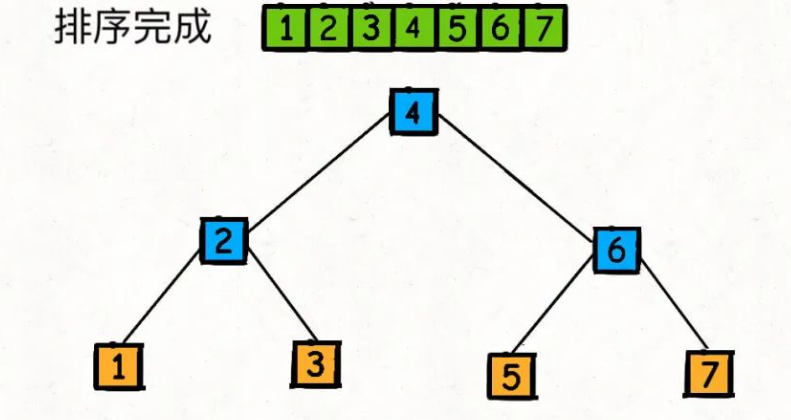
理解:快速排序的过程是一个构造二叉搜索树的过程
因为 partition 函数每次都将数组切分成左小右大两部分,恰好和二叉搜索树左小右大的特性吻合
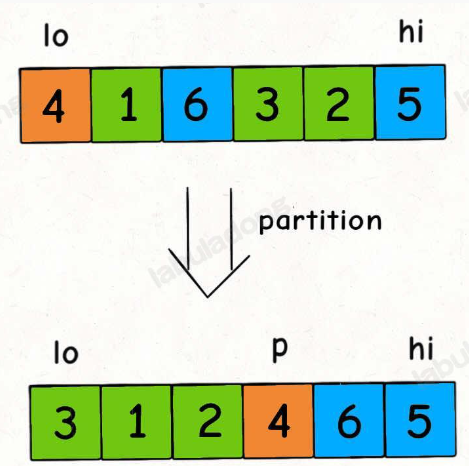
快速排序的核心无疑是 partition 函数, partition 函数的作用是在 nums[lo..hi] 中寻找一个分界点 p,通过交换元素使得 nums[lo..p-1] 都小于等于 nums[p],且 nums[p+1..hi] 都大于 nums[p]:
我们为了避免出现构造二叉搜索树时不平衡状态下退化为链表这种极端情况,需要引入随机性。
常见的方式是在进行排序之前对整个数组执行 洗牌算法进行打乱,或者在 partition函数中随机选择数组元素作为分界点,本文会使用前者。
代码实现
class Quick {
public static void sort(int[] nums) {
// 为了避免出现耗时的极端情况,先随机打乱
shuffle(nums);
// 排序整个数组(原地修改)
sort(nums, 0, nums.length - 1);
}
private static void sort(int[] nums, int lo, int hi) {
if (lo >= hi) {
return;
}
// 对 nums[lo..hi] 进行切分
// 使得 nums[lo..p-1] <= nums[p] < nums[p+1..hi]
int p = partition(nums, lo, hi);
sort(nums, lo, p - 1);
sort(nums, p + 1, hi);
}
// 对 nums[lo..hi] 进行切分
private static int partition(int[] nums, int lo, int hi) {
int pivot = nums[lo];
// 关于区间的边界控制需格外小心,稍有不慎就会出错
// 我这里把 i, j 定义为开区间,同时定义:
// [lo, i) <= pivot;(j, hi] > pivot
// 之后都要正确维护这个边界区间的定义
int i = lo + 1, j = hi;
// 当 i > j 时结束循环,以保证区间 [lo, hi] 都被覆盖
while (i <= j) {
while (i < hi && nums[i] <= pivot) {
i++;
// 此 while 结束时恰好 nums[i] > pivot
}
while (j > lo && nums[j] > pivot) {
j--;
// 此 while 结束时恰好 nums[j] <= pivot
}
// 此时 [lo, i) <= pivot && (j, hi] > pivot
if (i >= j) {
break;
}
swap(nums, i, j);
}
// 将 pivot 放到合适的位置,即 pivot 左边元素较小,右边元素较大
swap(nums, lo, j);
return j;
}
// 洗牌算法,将输入的数组随机打乱
private static void shuffle(int[] nums) {
Random rand = new Random();
int n = nums.length;
for (int i = 0 ; i < n; i++) {
// 生成 [i, n - 1] 的随机数
int r = i + rand.nextInt(n - i);
swap(nums, i, r);
}
}
// 原地交换数组中的两个元素
private static void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
快速排序理想情况的时间复杂度是 O(NlogN),空间复杂度 O(logN),极端情况下的最坏时间复杂度是 O(N^2),空间复杂度是 O(N)。
快速排序是「不稳定排序」,与之相对的,前文讲的 归并排序是「稳定排序」。
对于序列中的相同元素,如果排序之后它们的相对位置没有发生改变,则称该排序算法为「稳定排序」,反之则为「不稳定排序」。
比如说你有若干订单数据,已经按照订单号排好序了,现在你想对订单的交易日期再进行排序:
如果用稳定排序算法(比如归并排序),那么这些订单不仅按照交易日期排好了序,而且相同交易日期的订单的订单号依然是有序的。
但如果你用不稳定排序算法(比如快速排序),那么虽然排序结果会按照交易日期排好序,但相同交易日期的订单的订单号会丧失有序性。
为什么快速排序是不稳定排序,而归并排序是稳定排序呢?
稳定性是指待排序元素中相等的元素在排序后相对位置不变。想象下两个相等元素在快排的树中,位置靠前的那个被拿到P位置,那么这两个元素的相对位置就变了,最终排序结果就是不稳定的。但如果是在归并排序树中,每次都将元素们对半分开再按大小合并,即使相等元素被放入左右两个子树,只要最后按原来元素位置顺序遍历合并,就能保证相等元素的相对位置跟原来一样,所以归并排序可以是稳定的
快速选择算法(Quick Select)-- 变体
215. 数组中的第K个最大元素
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
题目要求我们寻找第 k 个最大的元素,稍微有点绕,意思是去寻找 nums 数组降序排列后排名第 k 的那个元素。
这种问题有两种解法,一种是二叉堆(优先队列)的解法,另一种就是快速选择算法,我们分别来看。
二叉堆(优先队列)解法
class Solution {
public int findKthLargest(int[] nums, int k) {
// 小顶堆,堆顶是最小元素
PriorityQueue<Integer> pq = new PriorityQueue<>();
for (int e : nums) {
// 每个元素都要过一遍二叉堆
pq.offer(e);
// 堆中元素多于 k 个时,删除堆顶元素
if (pq.size() > k) {
pq.poll();
}
}
// pq 中剩下的是 nums 中 k 个最大元素,
// 堆顶是最小的那个,即第 k 个最大元素
return pq.peek();
}
}
核心思路就是把小顶堆 pq 理解成一个筛子,较大的元素会沉淀下去,较小的元素会浮上来;当堆大小超过 k 的时候,我们就删掉堆顶的元素,因为这些元素比较小,而我们想要的是前 k 个最大元素嘛。当 nums 中的所有元素都过了一遍之后,筛子里面留下的就是最大的 k 个元素,而堆顶元素是堆中最小的元素,也就是「第 k 个最大的元素」。
快速选择算法
题目问「第 k 个最大的元素」,相当于数组升序排序后「排名第 n - k 的元素」,为了方便表述,后文另 k' = n - k。
我们刚说了,partition 函数会将 nums[p] 排到正确的位置,使得 nums[lo..p-1] < nums[p] < nums[p+1..hi]:
这时候,虽然还没有把整个数组排好序,但我们已经让 nums[p] 左边的元素都比 nums[p] 小了,也就知道 nums[p] 的排名了。
那么我们可以把 p 和 k' 进行比较,如果 p < k' 说明第 k' 大的元素在 nums[p+1..hi] 中,如果 p > k' 说明第 k' 大的元素在 nums[lo..p-1] 中。
// 快速选择算法
class Solution {
public int findKthLargest(int[] nums, int k) {
// 首先随机打乱数组
shuffle(nums);
int lo = 0, hi = nums.length - 1;
// 转化成「排名第 k 的元素」
k = nums.length - k;
while (lo <= hi) {
// 在 nums[lo..hi] 中选一个分界点
int p = partition(nums, lo, hi);
if (p < k) {
// 第 k 大的元素在 nums[p+1..hi] 中
lo = p + 1;
} else if (p > k) {
// 第 k 大的元素在 nums[lo..p-1] 中
hi = p - 1;
} else {
// 找到第 k 大元素
return nums[p];
}
}
return -1;
}
// 对 nums[lo..hi] 进行切分
private static int partition(int[] nums, int lo, int hi) {
int pivot = nums[lo];
// 关于区间的边界控制需格外小心,稍有不慎就会出错
// 我这里把 i, j 定义为开区间,同时定义:
// [lo, i) <= pivot;(j, hi] > pivot
// 之后都要正确维护这个边界区间的定义
int i = lo + 1, j = hi;
// 当 i > j 时结束循环,以保证区间 [lo, hi] 都被覆盖
while (i <= j) {
while (i < hi && nums[i] <= pivot) {
i++;
// 此 while 结束时恰好 nums[i] > pivot
}
while (j > lo && nums[j] > pivot) {
j--;
// 此 while 结束时恰好 nums[j] <= pivot
}
// 此时 [lo, i) <= pivot && (j, hi] > pivot
if (i >= j) {
break;
}
swap(nums, i, j);
}
// 将 pivot 放到合适的位置,即 pivot 左边元素较小,右边元素较大
swap(nums, lo, j);
return j;
}
// 洗牌算法,将输入的数组随机打乱
private static void shuffle(int[] nums) {
Random rand = new Random();
int n = nums.length;
for (int i = 0 ; i < n; i++) {
// 生成 [i, n - 1] 的随机数
int r = i + rand.nextInt(n - i);
swap(nums, i, r);
}
}
// 原地交换数组中的两个元素
private static void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
随机化之后的快速选择算法的复杂度可以认为是 O(N)。
这道题目与👆相同
剑指 Offer II 076. 数组中的第 k 大的数字
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
class Solution {
public int findKthLargest(int[] nums, int k) {
// 小顶堆,堆顶是最小元素
PriorityQueue<Integer> pq = new PriorityQueue<>();
for (int e : nums) {
// 每个元素都要过一遍二叉堆
pq.offer(e);
// 堆中元素多于 k 个时,删除堆顶元素
if (pq.size() > k) {
pq.poll();
}
}
// pq 中剩下的是 nums 中 k 个最大元素,
// 堆顶是最小的那个,即第 k 个最大元素
return pq.peek();
}
}
–end–