LeetCode 785. Is Graph Bipartite【DFS,二分图】中等

news2024/11/28 12:33:41

本文属于「征服LeetCode」系列文章之一，这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁，本系列将至少持续到刷完所有无锁题之日为止；由于LeetCode还在不断地创建新题，本系列的终止日期可能是永远。在这一系列刷题文章中，我不仅会讲解多种解题思路及其优化，还会用多种编程语言实现题解，涉及到通用解法时更将归纳总结出相应的算法模板。

为了方便在PC上运行调试、分享代码文件，我还建立了相关的仓库：https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中，你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等，还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解，还可以一同分享给他人。

由于本系列文章的内容随时可能发生更新变动，欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。

There is an undirected graph with n nodes, where each node is numbered between 0 and n - 1. You are given a 2D array graph, where graph[u] is an array of nodes that node u is adjacent to. More formally, for each v in graph[u], there is an undirected edge between node u and node v. The graph has the following properties:

There are no self-edges (graph[u] does not contain u).
There are no parallel edges (graph[u] does not contain duplicate values).
If v is in graph[u], then u is in graph[v] (the graph is undirected).
The graph may not be connected, meaning there may be two nodes u and v such that there is no path between them.

A graph is bipartite if the nodes can be partitioned into two independent sets A and B such that every edge in the graph connects a node in set A and a node in set B.

Return true if and only if it is bipartite.

Example 1:

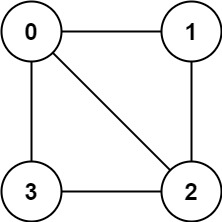
Input: graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
Output: false
Explanation: There is no way to partition the nodes into two independent sets such that every edge connects a node in one and a node in the other.

Example 2:

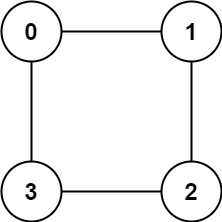
Input: graph = [[1,3],[0,2],[1,3],[0,2]]
Output: true
Explanation: We can partition the nodes into two sets: {0, 2} and {1, 3}.

Constraints:

graph.length == n
1 <= n <= 100
0 <= graph[u].length < n
0 <= graph[u][i] <= n - 1
graph[u] does not contain u.
All the values of graph[u] are unique.
If graph[u] contains v, then graph[v] contains u.

题意：存在一个 无向图 ，图中有 n 个节点。其中每个节点都有一个介于 0 到 n - 1 之间的唯一编号。给你一个二维数组 graph ，其中 graph[u] 是一个节点数组，由节点 u 的邻接节点组成。形式上，对于 graph[u] 中的每个 v ，都存在一条位于节点 u 和节点 v 之间的无向边。该无向图同时具有以下属性：

不存在自环（graph[u] 不包含 u）。
不存在平行边（graph[u] 不包含重复值）。
如果 v 在 graph[u] 内，那么 u 也应该在 graph[v] 内（该图是无向图）
这个图可能不是连通图，也就是说两个节点 u 和 v 之间可能不存在一条连通彼此的路径。

二分图 定义：如果能将一个图的节点集合分割成两个独立的子集 A 和 B ，并使图中的每一条边的两个节点一个来自 A 集合，一个来自 B 集合，就将这个图称为 二分图 。

如果图是二分图，返回 true ；否则，返回 false 。

解法 DFS染色判断二分图

二分图的节点可以分成两个集合，集合内的点之间没有边，任意一条边的两个节点属于不同集合，可以为图中各个节点着色，两个集合的节点分别涂成两种颜色。如果图中任何一条边的两个节点都可以被涂成不同的颜色，则该图就为二分图。

一个图可能包含多个子图，需要逐次对每个子图涂色。需要一个数组 colors 标记所有节点的颜色，规定 $0$ 表示当前未涂色， $1$ 表示第一种颜色， $2$ 表示第二种颜色。为了给所有的节点着色，需要遍历图内的所有结点，在着色的过程中若碰到「已着色、但不符合一条边两个节点不同颜色」的情况，即可判断该图不可能是二分图。

遍历图的所有结点可以使用两种方式，即广度优先搜索和深度优先搜索。这里用DFS，比较简洁：

class Solution {
public:
    bool isBipartite(vector<vector<int>>& graph) {
        int n = graph.size();
        vector<int> color(n);
        function<bool(int, int)> dfs = [&](int i, int c) {
            color[i] = c; // 1,2表示访问过,0表示未访问
            for (int j : graph[i]) {
                if (!color[j] && dfs(j, 3 - c) == false) return false;
                else if (color[j] == color[i]) {  return false; }
            }
            return true;
        };
        for (int i = 0; i < n; ++i)
            if (!color[i] && dfs(i, 1) == false) return false;
        return true;
    }
};