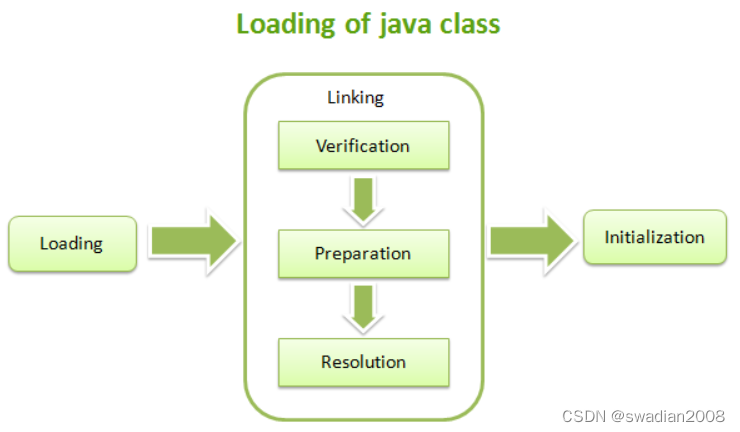
一、论文简述
1. 第一作者:Mattia Rossi
2. 发表年份:2023
3. 发表期刊:WACV
4. 关键词:MVS、3D重建、极线搜素
5. 探索动机:目前的方法无论是深度值还是逆深度值,都需要提前确定深度值范围,影响重建效果还增加内存开销。
The second is the need to discretize the depth search space, which requires both to define a depth range of interest and to define a discretization scheme for it. Although the depth range can be inferred from the sparse reconstruction of a Structure from Motion (SfM) system, the sparse nature of the reconstruction can lead to under or over estimate the
depth range of the portion of the scene captured by a specific image, thus preventing the reconstruction of some scene areas. Moreover, some discretization strategies suit certain scenes better than others. For objects close to the camera, a fine grained discretization toward the depth range minimum is preferable. Conversely, objects farther in the distance can be reconstructed even with a coarser discretization. The limitations behind depth discretization approaches becomes obvious when considering scenes containing multiple objects at very different distances from the camera. A better alternative is represented by a discretization of the inverse depth range, but this still calls for a depth range of interest.
6. 工作目标:通过极限搜索,解决上述问题。
7. 核心思想:In order to tackle both of these disadvantages, we propose a new method for MVS depth estimation denoted Deep Epipolar Line Search (DELS). For each pixel in the reference image, we search for the matching point in the source image by exploring the corresponding epipolar line. The search procedure is carried out iteratively and utilizes bi-directional partitions of the epipolar line around the current estimate to update the predicted matching point. These updates are guided by a deep neural network, fed with features from both the reference and the source image.
- A deep, iterative and coarse-to-fine depth estimation algorithm operating directly on the epipolar lines, thus avoiding the drawbacks of depth discretization, e.g. no specification of a depth range is needed.
- A confidence prediction module and a geometry-aware fusion strategy that, coupled, permit a robust fusion of the multiple reference image depth maps from the different source images.
8. 实验结果:
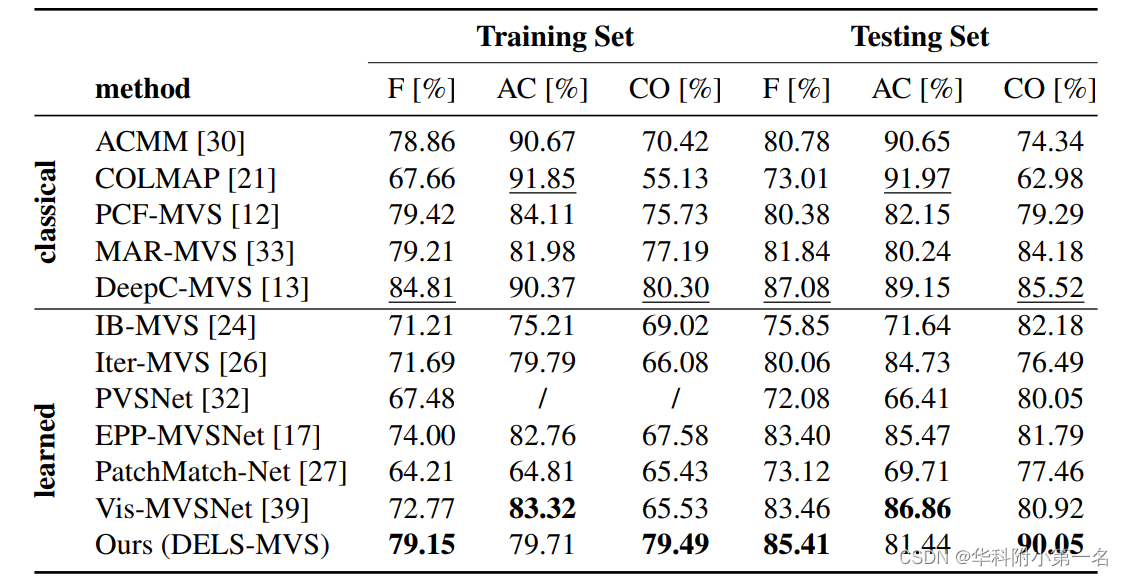
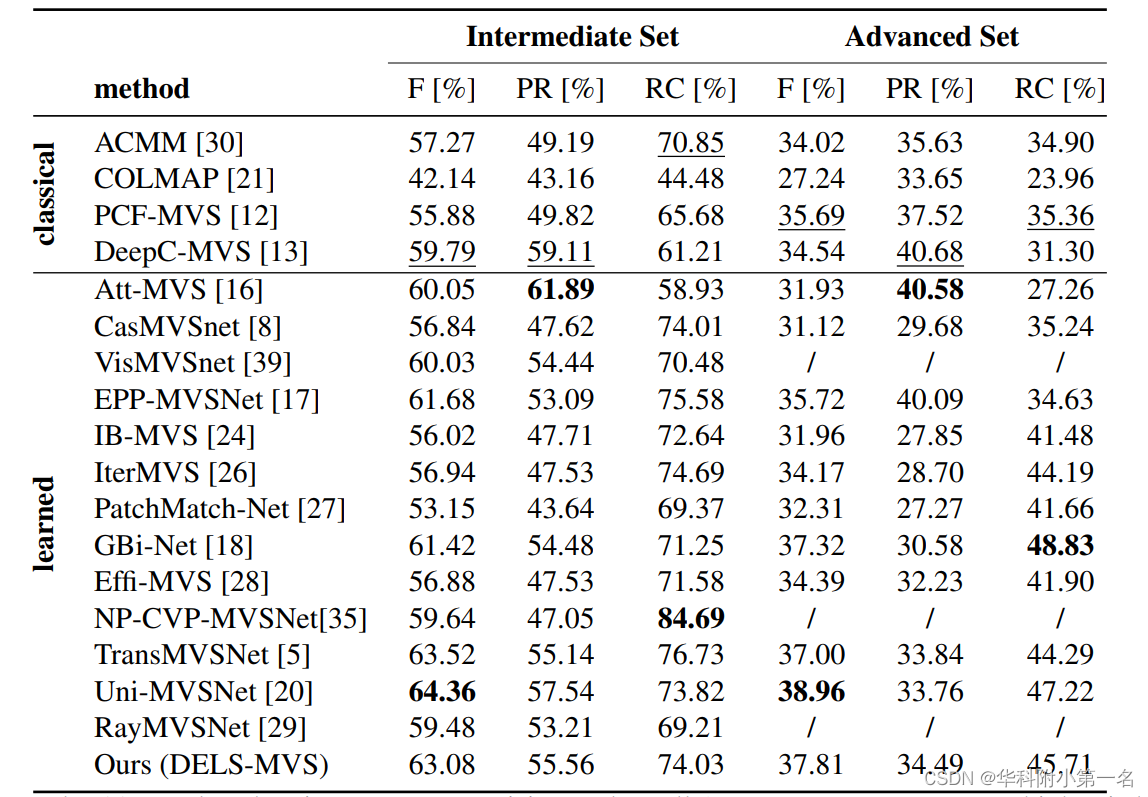
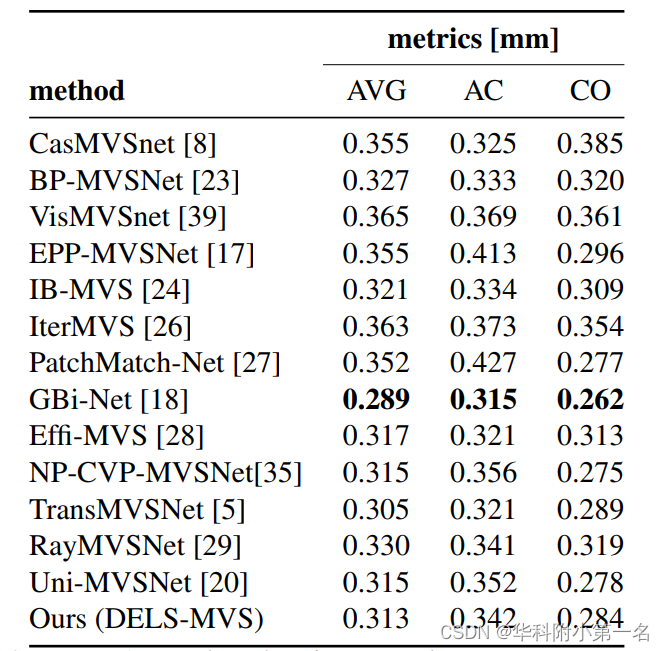
we verify the robustness of our method by evaluating on all the most popular MVS benchmarks, namely ETH3D, Tanks and Temples and DTU and achieve competitive results.
9.论文下载:
2212.06626.pdf (arxiv.org)
二、实现过程
1. DELS-MVS概述
系统以1张参考图像R和N≥1张源图像S0≤N≤N−1作为输入。首先,利用卷积神经网络从参考图像和给定源图像中提取深度特征,然后将这些特征输入至核心算法中,用于估计参考图像上的深度图Dn。对于每个参考图像像素,算法的目标是估计实际像素投影到源图像和作者沿极线的初始猜测之间的残差。为了避免尺度依赖,算法以粗到细的方式通过迭代分类步骤估计残差,算法命名为深度极线线搜索(DELS)。因为迭代分类类似于搜索,并利用了深度神经网络,称为极线残差网络(ER-Net)。最后,DELS-MVS还具有一个置信度网络(C-Net),它将置信度图与估计深度图Dn关联起来。
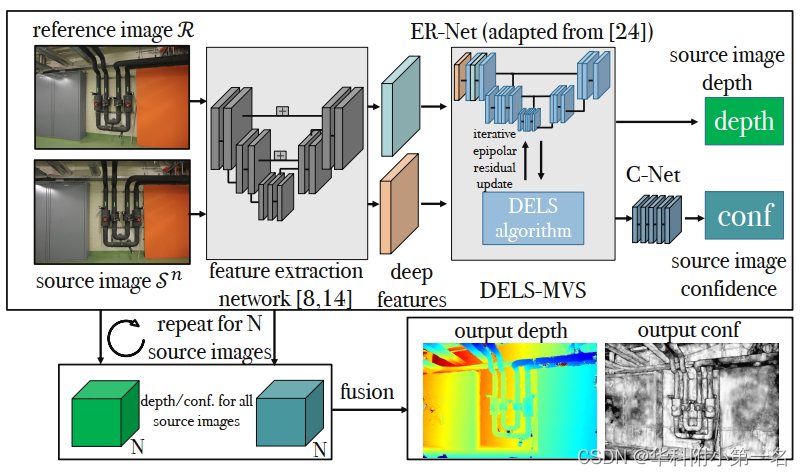
在提取深度特征后,深度极线搜索为每个源图像生成输出深度图和置信度图,然后融合成单个输出深度图。
2. 通过极线残差进行深度估计
DELS算法使用恒定深度图D0n初始化,其中常量为从运动结构恢复(SfM)系统获得的最小深度和最大深度范围之间的平均值。
给定参考图像中的一个像素(x, y),设pn0(x, y)为(x, y)根据初始深度Dn0(x, y)在源图像Sn上的投影。DnGT为真实深度图,设pn GT(x, y)为(x, y)根据DnGT (x, y)投影到源图像Sn中的值。两个投影都在同一极上行,如上图所示。目标是估计一维极线残差EGT n∈R,使下列关系成立:
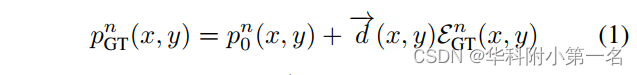
其中单位向量→d (x, y)∈R2定义极线方向。事实上,重要的是要观察到极线先天没有任何方向。特别地,我们确定方向→d (x, y),使(x, y)的深度假设在其方向上一致地移动,从而单调减小。为了完整起见,观察到下列关系是成立的:
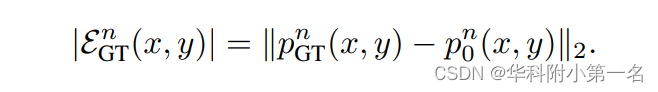
用En(x, y)表示由DELS估计的极线残差,Eq.(1)用于纠正原始估计pn0(x, y),产生pn(x, y)。残差现在可以使用给定的相对相机变换TR→Sn从参考源图像转换为原始像素(x, y)的深度值Dn(x, y)。这个过程如下图所示。
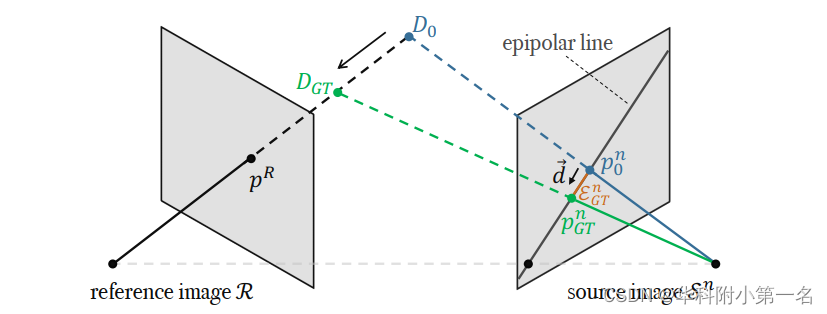
3. 深度极线线搜索(DELS)
在MVS中,无论是在同一个场景中还是不同场景中,不同源图像和参考图像之间的基线可能会有很大的变化。此外,深度图可以根据特定场景显示非常不同的范围:从非常小的范围(用于重建小物体)到非常大的范围(用于重建室外场景)。在大多数三维重建场景中,场景尺度是未知的。总的来说,这使得网络训练和直接回归视差,成为具有挑战性的任务。因此本文将极线残差估计问题重新定义成一个迭代的、从粗到细的分类方案。
本文用Eni(x,y)i=1,2,…表示迭代i后的极线残差估计。为了估计新迭代i的极线残差,将极线分割为k个分区L ={0,1,…,k−1},k为偶数,如下图所示。特别地,定义了两个分区集:内集LI ={1,…,k−2}和外集LO = {0, k−1}。通过公式1计算由Eni−1(x, y)得到的内集位于前一次迭代极线位置pn i−1(x, y)的中心。该集从左边界延伸到右边界,其中δi(x, y)∈R+表示每个分区的大小。外层集的分区0和k−1模拟了匹配项位于当前内部分区未覆盖的极线线段的情况,即在OiL(x, y)和OiR(x, y)所包围的段之外。因此,它们提供了下一次迭代中前进方向的估计。
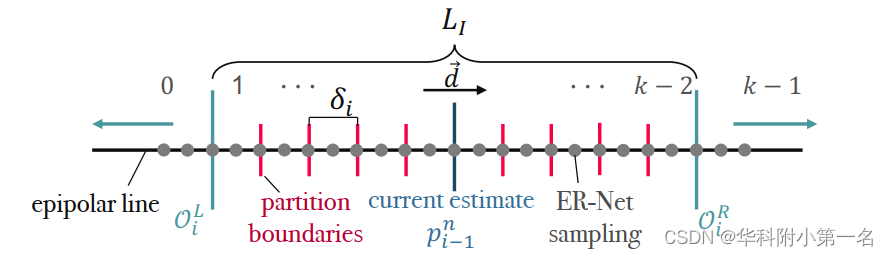
本文利用一个神经网络来预测分区l*i (x, y)∈l,它承载着真实值投影pn GT(x, y)。一旦确定了段,就可以计算出相对残差eni(x, y)∈R,并与之前的迭代残差en i−1(x, y)相加,得到当前迭代:
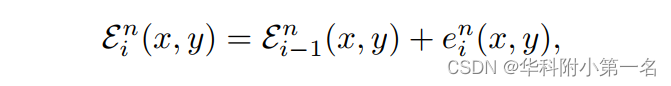
其中En0(x, y)=0。特别考虑了两种情况:
案例1:l*i(x, y)∈LI,这表明pn GT(x, y)将位于有限分区l*i (x, y)内的某个位置,因此pni(x, y)将被放置在其中点。
案例2:分区l*i(x, y)∈LO,它只提供了关于pn GT(x, y)搜索方向的一般提示,因此pn i (x, y)被放置在OLi(x,y)−δi(x,y)/2和ORi(x,y)+δi(x,y)/2对于l*i(x,y)=0和k−1。特别地,这个策略允许在前一个迭代中补偿不正确的预测,因为在当前和下一个迭代的内部分区之间保持了一些重叠。
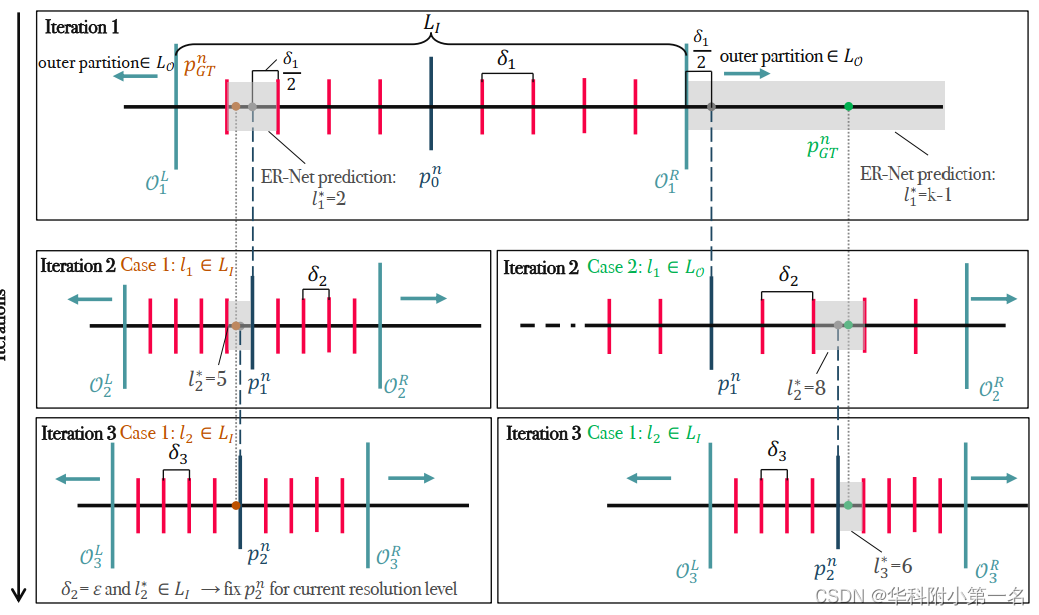
上图总结了这两个场景,其中有三个DELS迭代的草图。一般来说,该算法区分两种情况:在极线上的预测匹配是否位于内集LI(情况1)或外集LO(情况2)。这将改变分区宽度δi和下一个估计的位置,用于接下来的迭代。总的来说,对于预测分区l*i(x, y)∈l,概括的更新策略等价于如下定义相对残差:
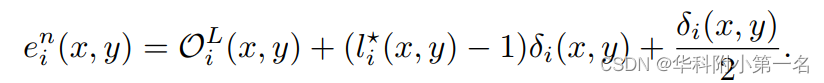
DELS从粗到细方案在每次迭代中更新分区宽度δi,再次区分Case1和2。事实上,在第一种场景中,分区宽度在迭代i + 1开始时减半,而在第二种场景中它保持不变:
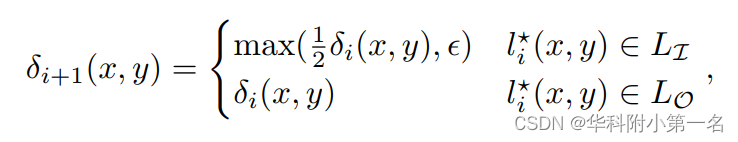
其中,ε∈R+是区间宽度的下限。最后,DELS采用多分辨率策略,j=0,1,2分别代表全分辨率,半分辨率和四分之一分辨率。层级上的迭代次数j表示Ij。层级j用前一个尺度j+1的上尺度的极线残差初始化,即Enj = NN↑(Ejn+1)·2,其中NN↑是最近的上采样算子。此外,当达到给定层级ϵj的分区宽度下界并且所选分区包含在内部集中时,对于给定像素的迭代将被中断,因为认为实现了极线残差的最大可实现精度。上图(迭代3,左边)举例说明了这种行为。
4. 极线残差网络
极线残差网络网络(ER-Net)进行每次DELS迭代的分类任务。ER-Net接收之前的迭代极线残差图Ein−1:这允许,对于每个参考图像像素(x, y),在最新估计pn i−1(x, y)周围的极线上对特征进行采样FSn。为此,将可变形卷积合并到一个改编的U-Net-like结构中。特别是,在U-Net的顶层,可变形核沿极线分布,并对齐,使其与在距离上等距的样本重叠,在pni−1(x,y)之前和之后的δi(x, y)/2。在这种设置中,内集中的样本落在每个分区的开始点、中间点和结束点。采样方案由上图中的灰点表示。选择核大小来覆盖内部集合中的所有样本,并进一步扩展到外部集合。特别地,设置k= 12,内核大小为5,产生5×5=25个样本。对于低分辨率层级的U-Net,保持与最高层级相同的分区宽度和内核大小,因为这增加了网络感受野。
网络输出的多通道输出层输入到一个softmax激活层,该激活层为k个分区中的每一个分区li(x, y)∈L产生一个概率:
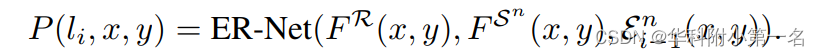
推理时,选择softmax概率最大的分区:
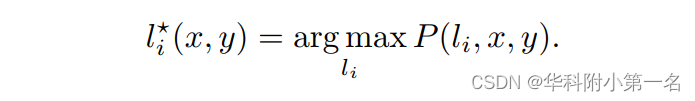
在涉及全分辨率、半分辨率和四分之一分辨率的多分辨率方案中采用ER-Net,但不共享层级之间的参数。
5. 置信度网络
该方法在参考图像上计算N个深度图,每个图使用不同的源图像计算。这就提出了如何利用所有估计的深度图将它们融合到一个单一的深度图的问题,因为一些参考图像区域可能在一个源图像中可见,而在另一个源图像中不可见。为此,引入了一个置信度网络(C-Net),用于将一个置信度图Cn指定给每个估计深度图Dn:然后使用置信度图来指导多个可用深度图的融合。
在多分辨率方案的每个层级j上,计算了一个类似于分区概率的像素级熵的图,但考虑了它在DELS迭代中的演化:
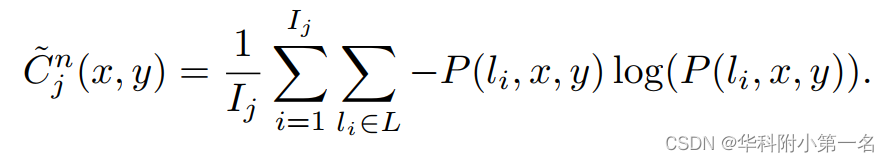
用C~n=NN↑(C~n2)+NN↑(C~n1)+C~n0来监督C-net,这考虑到了不同的分辨率层级。此外,将C ~(x,y)设置为最后一次迭代中估计分区具有lI*(x, y)∈LO属性的位置的最大熵值。这包含了与外部集合LO相关的最后一次迭代中的预测产生不可靠的深度估计的知识,表明存在遮挡。C-Net体系结构由4个卷积层(核大小为3,leaky ReLU激活)和一个sigmoid激活输出,生成范围为[0,1]的Cn。
6. 几何感知多视图融合
在每个像素(x, y)上,有一组N个深度候选,每个源图像对应一个。深度候选Dn(x, y)与DELS算法预测的最终极线的线分区的中心相关联,分区长度对应于场景中大小为∆Dn(x, y)∈R的深度范围。值得注意的是,尽管在不同的源图像上,极线分区具有相同的长度,但源图像与源图像之间对应的深度范围∆Dn(x, y)有所不同,这取决于源摄像机与参考摄像机之间的几何关系。在该方法中,利用这一关键事实,提出了一种利用学习的置信度的几何感知融合方案。特别地,深度候选的关联分区具有足够的置信度和较窄的深度范围,因为它们对应于可靠且细粒度的深度预测。
因此,融合过程如下所示。首先,我们确定置信度大于阈值ω的候选集合Nω。然后,我们选择分区深度最小的候选者,即Dn*(x, y),其中n*= argnmin∆Dn(x, y),n∈Nω(Nω为空,选择置信度最高的)。最终深度是在相对距离阈值内来自Dn*(x, y)所有候选的平均值η,引入掩码:

最终输出深度值可表示为:
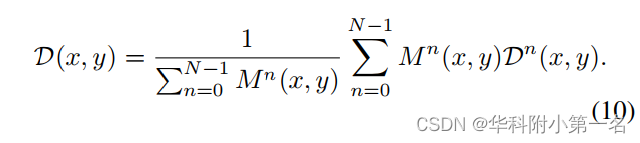
7. 实验
7.1. 实现细节
使用PyTorch实现,并使用批大小为1的ADAM优化器进行训练。
7.2. 与先进技术的比较