因为学机器学习的时候发现自己线性代数忘光光了(悲😓,本篇捞一捞当年学线性代数看哔哩哔哩宋浩老师补充记的潦草笔记。
目录
📚线性代数知识点
🐇向量
🥕向量的线性组合
🥕线性相关无关的性质
🥕线性相关无关的定理
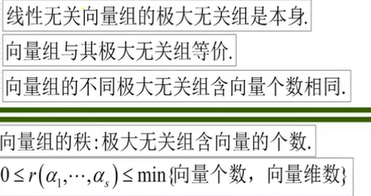
🥕极大线性无关组
🐇方程组
🥕线性方程组有解判定
🥕方程组解的结构
🐇矩阵
🥕矩阵的运算
🥕逆矩阵
🥕矩阵的初等变换:交换,数乘,倍加
🥕矩阵的秩
🥕伴随矩阵
🐇行列式
🥕行列式的重要性质
🥕行列式的求解
🥕行列式应用
🐇 二次型
🥕二次型的定义
🥕标准型
🥕规范型
🐇 特征值和特征向量
🥕特征值和特征向量
🥕相似对角化
🥕内积
🥕正交和正交相似
🥕实对称矩阵的对角化(实对称矩阵一定能对角化)
🥕正定矩阵
🥕最小二乘问题
🥕QR分解
🐇 知识串联
🥕特征值相同
🥕两矩阵相似的条件
🥕矩阵A可逆
🥕矩阵合同
🥕归纳等价、相似、合同矩阵
🥕线性代数中的提公因子
🥕初等变换总结
🥕关于正定矩阵之类
📚线性代数知识点
🐇向量
🥕向量的线性组合

🥕线性相关无关的性质

🥕线性相关无关的定理

🥕极大线性无关组
🐇方程组
🥕线性方程组有解判定
AX=B
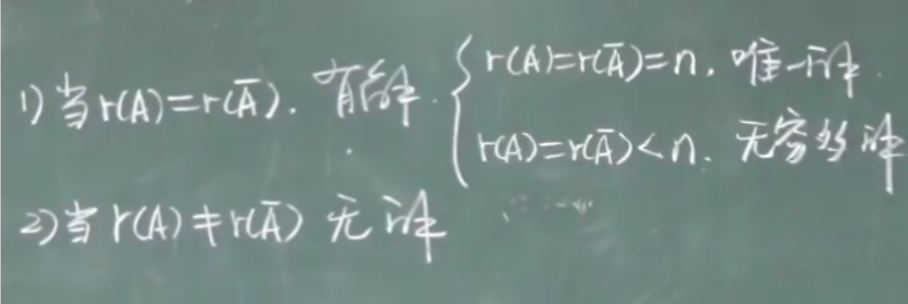
AX=0

🥕方程组解的结构
AX=0

AX=B

🐇矩阵
🥕矩阵的运算
补充矩阵乘法条件记忆:中间相等

重点关注:
- AB一般不等于BA:说明左右顺序不互换,在左边乘就一起在左边乘。
- AB=AC且A≠0,推不出B=C:如果补充A可逆,则有AB=AC,可推出B=C
- AB=0推不出A=0或B=0:如果AB都是方阵,那么由AB=0,可以推出|A|=0或者|B|=0;在后边kα=0,可以推出k=0或者α=0S
- (AB)² ≠ A²B²
- 转置和逆的一些比较

🥕逆矩阵

逆矩阵的定义,本身不常用,但关注它的推论:如果AB=E,那么A,B均可逆,且互逆。
推论应用证明思路:已知(A+E)的逆=Y,最后即证(A+E)Y=E(若有相关系数则左移)

A可逆的所有充要条件

🥕矩阵的初等变换:交换,数乘,倍加

初等变换总结:
- ①求A逆,只做初等行变换
- ②求矩阵的秩,把A化成阶梯型(行列皆可),非零行有几行它的秩就是几
- ③求a1,a2,....的极大线性无关组,把这些向量列成列,只做初等行变换,行简化阶梯型
- ④求Ax=0的解,只对A做初等行变换
- ⑤求Ax=B的解,只对增广矩阵做初等行变换
- ⑥求特征向量,对齐次线性方程组,只做初等行变换
- ⑦化二次型对A,E做相同初等列变换;只对A做相应的初等行变换。这个相应是和列变换相应。即列变换和行变换是一套的,配套进行,做完一个列变换,马上做对应的行变换
🥕矩阵的秩

对于n阶矩阵,AB=0,则有r(A)+r(B)≤n
r(AB) ≤ min{r(A),r(B)}
相关题型
- Ax=0,基础解系,n-r(A)
- 求向量组的秩:把向量组成矩阵,矩阵的秩就是向量组的秩
- 在特征向量中假设λi是矩阵A的Ni重特征值,则A与∧相似<=>r(A-λiE)=N-Ni(i=1,2,…,N)
🥕伴随矩阵

🐇行列式
🥕行列式的重要性质

矩阵的逆的行列式 = 1/矩阵行列式
伴随矩阵的行列式 = 矩阵行列式的n-1次
转置的行列式等于它本身
det(kA)=k的n次det(A)
- 某一行(列)有公因子k,k外提一次;所有行(列)有公因子k,k外提n次。
两行(列)的元素相等,D=0;两行(列)元素成比例,D=0;某一行(列)的元素全为0,D=0;
- 不过D=0不能反推标蓝条件。但D=0可以说明,该矩阵降秩,不可逆,其行(列)向量组线性相关。
🥕行列式的求解
①纯数的行列式,化为上三角
②带字母的行列式
- 某一行(列)尽可能化出0,按行展开
- 拉普拉斯定理:任取k行(列),由这k行(列)元素组成的所有k阶子式与其代数余子式乘积之和=D。

- 上下项相同的看看能不能化到三角行列式。

③简化计算:及时提取公因数到外边
④特殊行列式

- 范德蒙行列式
- 克莱姆法则
🥕行列式应用
①Ax=0(n方程n未知数),有非零解,则 |A|=0;
②n个n维向量组,判断线性相关/无关——|A|=0得线性相关;反之无关。
③判断A可逆,|A|≠0
④求 A逆=伴随矩阵/A的行列式(不常用)
⑤二次型正定判断,各阶顺序主子式都大于零

🐇 二次型
🥕二次型的定义
简单理解就是次数为二次
二次型→矩阵表达式
- 平方项的系数直接做成主对角元素
- 交叉项的系数除以2放到两个对称的相应位置上(相应位置为ij和ji位置)。所求的矩阵A即称为二次型的矩阵,它一定是对称的。即A转置等于A。
- 前头写上(x1 x2 x3...)后头写上竖着的(x1 x2 x3)
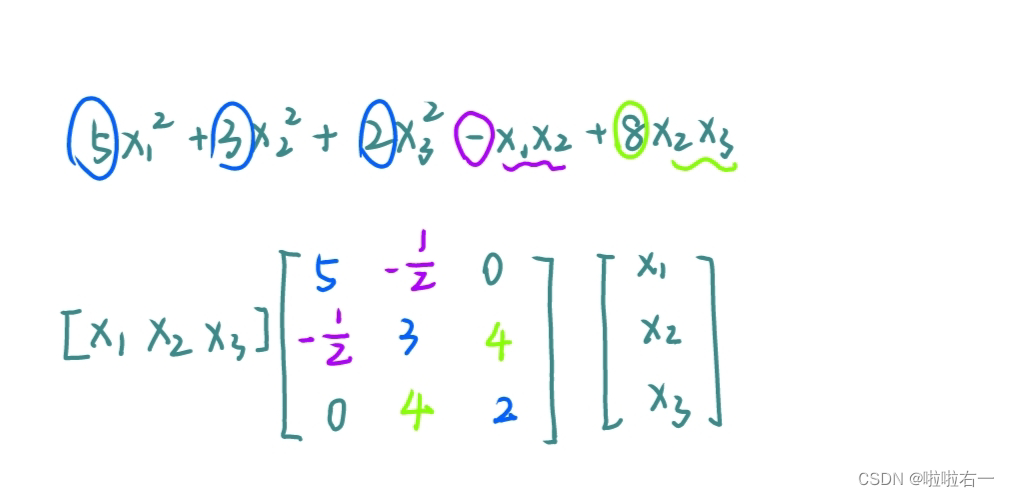
矩阵→二次型
- 主对角线元素直接作为平方项的系数
- 取主对角线右上角元素乘以2作为交叉项系数,至于跟的是X几,就看几行几列。如上图的逆过程,主对角线右上角有三个数,以4为例子,它在二行三列,所以对应为8X2X3。
- 直接进行上面两步的前提是已知是二次型的矩阵,即需要观察是否对称。至于不对称的那两个位置,把两个数相加除以2再分别写到原来的那两个位置,然后再按上述①②步计算。
🥕标准型
只有平方项,而平方项的系数可取任意值
把二次型转换为标准型(优质博客补充)
法一:配方法
- 注意:先配x1,再配x2,以此类推。而x1配完之后,后边就就不要再出现x1。
- 写出替换,但线性替换的格式一定是X=CY。
- 如果只有交叉项:换元,前边两个一加一减,后边保持原样。思想就是构造出平方项。
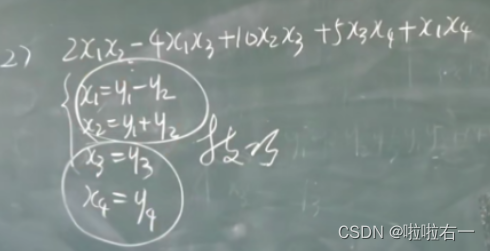
法二:初等变换
- 对A,E做相同初等列变换;
- 只对A做相应的初等行变换。这个相应是和列变换相应。即列变换和行变换是一套的,配套进行,做完一个列变换,马上做对应的行变换
- A化成对角矩阵时,E化成的就是C。
法三:正交替换(就正交化过程)(计算量复杂,在这里很少用)
- ①求特征值
- ②求特征向量
- ③将特征向量正交化单位化
- ④由③步骤后的特征向量写出目标矩阵,拿特征值写出对角形
- ⑤用最后所得的那个对角形拿来写标准型
🥕规范型
定义:全是二次项,系数为1的在前面,系数为-1的在后面,0在最后。
规范型的秩:1和-1的总数
- 正惯性指数:正项数(规范型中1的个数)
- 负惯性指数:负项数(规范型中-1的个数)
- 合同的矩阵,负惯性指数和正惯性指数都相同
- 符号差:正惯性指数-负惯性指数
合同:A,B为两个n阶对称方阵,若存在一个可逆方阵,使得C'AC=B(C'代表的是C的转置矩阵)称A与B是合同的。任意一实对称方阵都合同与一个对角方阵。

🐇 特征值和特征向量
🥕特征值和特征向量
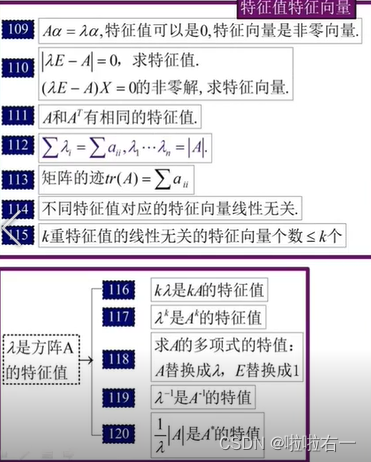
假设λi是矩阵A的Ni重特征值,则A与∧相似<=>r(A-λiE)=N-Ni(i=1,2,…,N)
- 例:
- λ1 = -1是一重根,r(A-(-1)E)=r(A+E)=3-1=2
- λ2 = λ3 = 1是2重根,r(A-E)=3-2=1
🥕相似对角化

🥕内积

施密特正交化
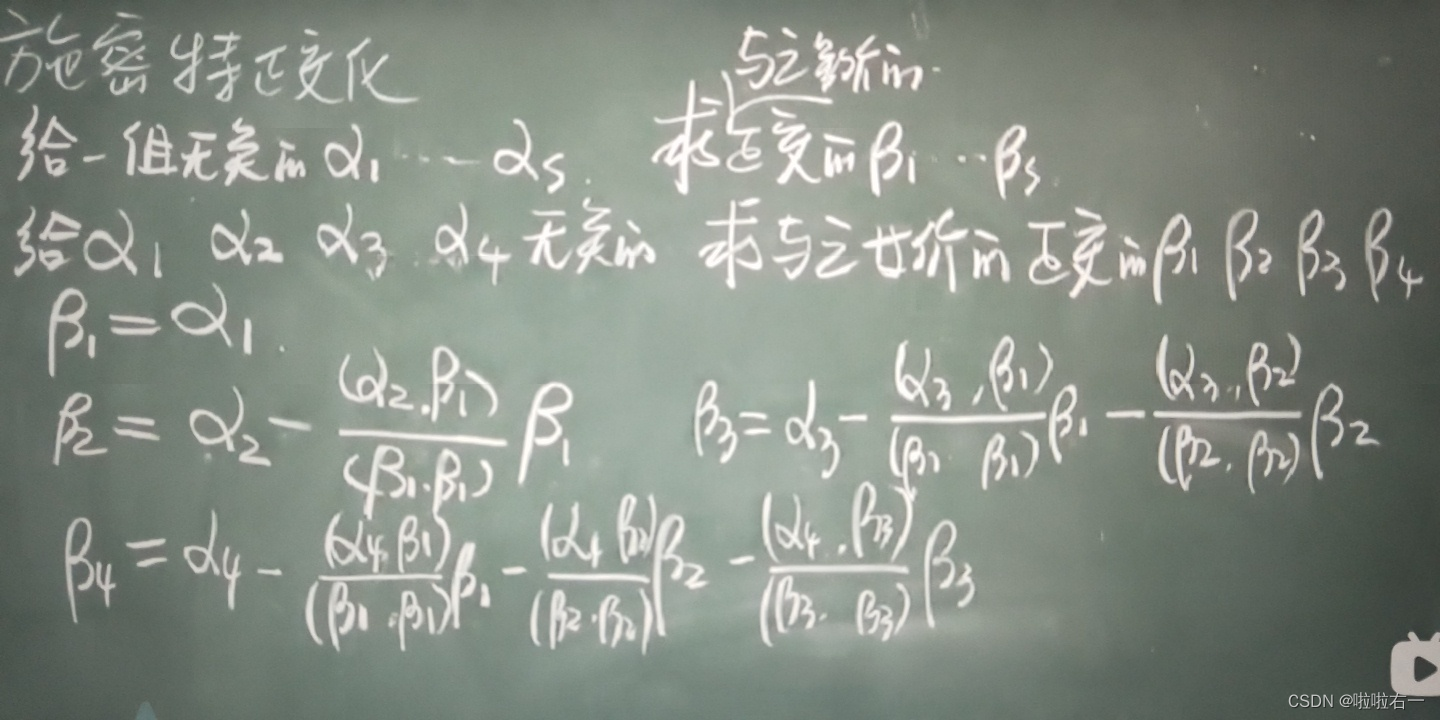
🥕正交和正交相似
正交矩阵A逆=A转置
A、B为实对称矩阵,则A、B相似的充要条件是A、B有相同的特征值
🥕实对称矩阵的对角化(实对称矩阵一定能对角化)
实对称矩阵对角化过程:给定实对称矩阵A,求正交Q,和对角形矩阵
①求特征值
②求特征向量
③特征向量正交化,单位化(正交化过程关注不同特征值的特征向量必正交)
④做成列,构成Q,写出对角形
🥕正定矩阵

判定方法:求出A的所有特征值。若A的特征值均为正数,则A是正定的;若A的特征值均为负数,则A为负定的。
🥕最小二乘问题
对于一个无解的Ax=b,找一个近似。一般的最小二乘问题就是找出使||b-Ax||尽量小的x。
求解过程(核心式子):

🥕QR分解
定理:如果m×n矩阵A的列线性无关,那么A可以分解为A=QR
过程

用QR分解的一个求解最小二乘问题的方法
①正交化操作
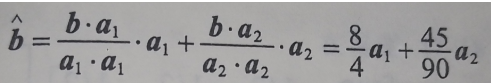
②直接取值
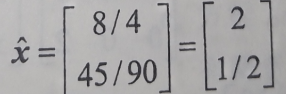
🐇 知识串联
🥕特征值相同
不一定相似,也不一定合同。(重数问题)但是:
- 1)如果都是对称矩阵,那么特征值相同,能推出合同
- 2)如果两矩阵都可以相似对角化,则两矩阵特征值相同,能推出相似。(基于相似的传递性)
- 特征值全为正的实对称矩阵——正定矩阵
🥕两矩阵相似的条件

- 秩相等
- 行列式值相等
- 迹数相等
判断相似的一般步骤
- ①若特征值不同则一定不相似。
- ②若特征值相同,看有无重特征值。无则相似。
- ③若有重特征值λi,是否r(λiE-A)=n-ni,是则相似。
从对角化直接判断相似

- 假设λi是矩阵A的Ni重特征值,则A与∧相似<=>r(A-λiE)=N-Ni(i=1,2,…,N)
- 对于上三角(或者是下三角)它的对角线即为其特征值。而已知一个矩阵和它相似,则立马可得该矩阵的特征值。注意这个性质,避免重复低效计算。
-
🥕矩阵A可逆
- A的行列式不为0
- A可表示为有限个初等矩阵相乘
- A行等价于n阶单位矩阵
- 矩阵的秩等于n
- A的列(行)向量组线性无关
- 齐次线性方程组Ax=0仅有零解
- 非齐次线性方程组Ax=b有解
- A的特征值都不为0
🥕矩阵合同
- 正负惯性指数相同
- 秩相同
- 特征值是相同的,行列式也是一样的,相似就合同,迹(两个矩阵主对角线的和)是一样的
🥕归纳等价、相似、合同矩阵
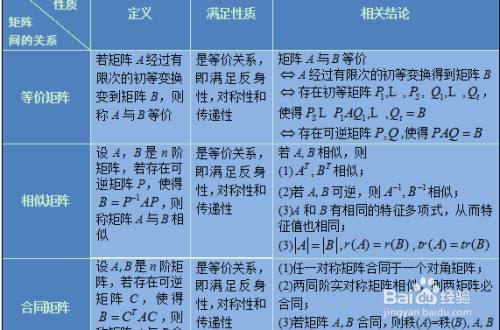
🥕线性代数中的提公因子

🥕初等变换总结
- ①求A逆,只做初等行变换
- ②求矩阵的秩,把A化成阶梯型(行列皆可),非零行有几行它的秩就是几
- ③求a1,a2,....的极大线性无关组,把这些向量列成列,只做初等行变换,行简化阶梯型
- ④求Ax=0的解,只对A做初等行变换
- ⑤求Ax=B的解,只对增广矩阵做初等行变换
- ⑥求特征向量,对齐次线性方程组,只做初等行变换
- ⑦化二次型对A,E做相同初等列变换;只对A做相应的初等行变换。这个相应是和列变换相应。即列变换和行变换是一套的,配套进行,做完一个列变换,马上做对应的行变换
🥕关于正定矩阵之类