- 梯度下降

- 我们可以用一种更系统的方法,来找到一组w,b,使成本函数的值最小。这个方法叫梯度下降算法,它可用于最小化任何函数,不仅仅包括线性回归的成本函数,也包括两个以上参数的其他成本函数
- 在线性回归中,w和b的初始值是多少并不重要,所以通常将他们的初始值设为0。
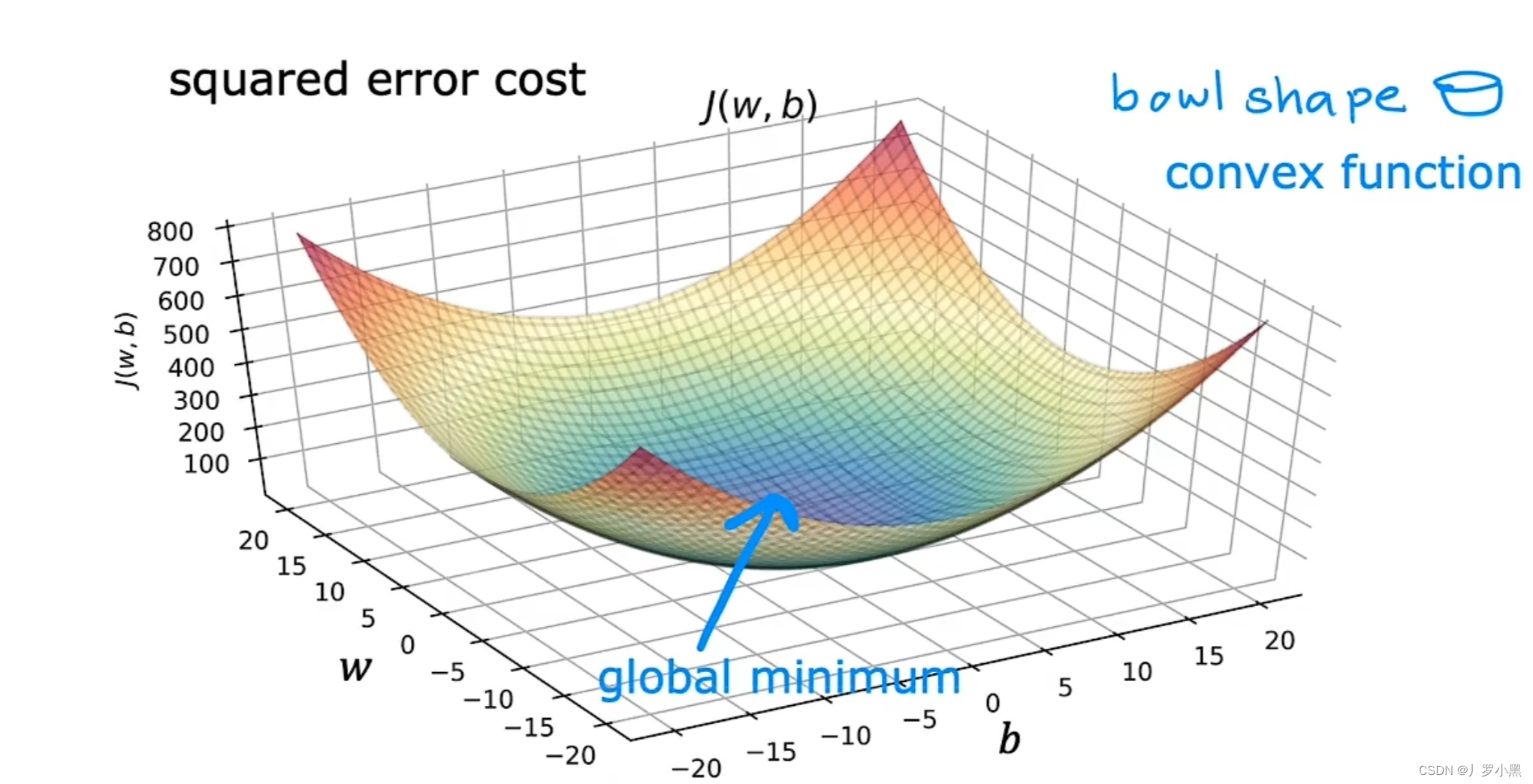
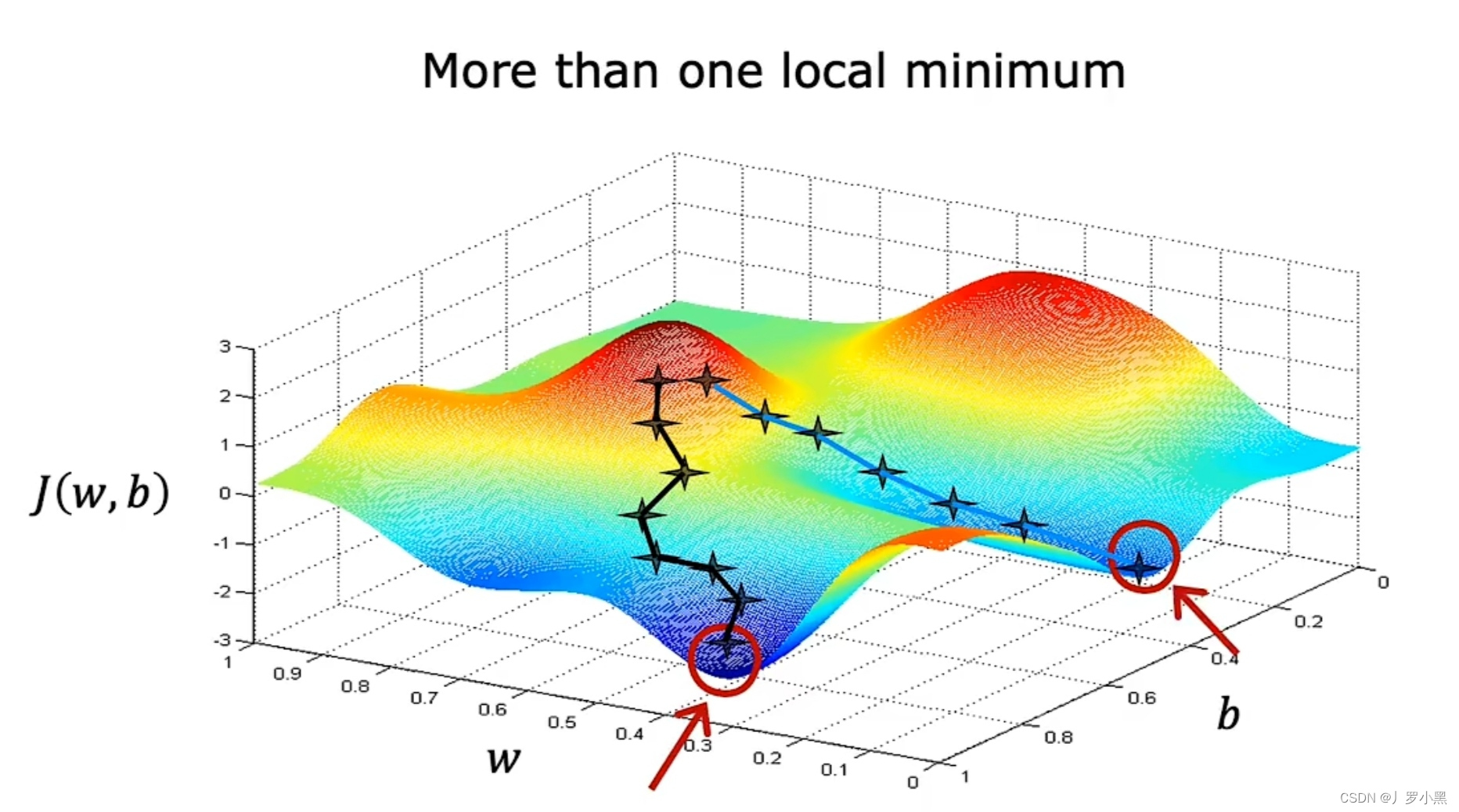
- 成本函数并不总是弓形或吊床行的函数,这代表他可能有两个及以上的最小值
- 梯度下降算法的步骤:
a. 初始化w和b的值,通常设为0
b. 继续更改w和b的值,来降低J函数的值
c. 直到J函数到达,或接近J函数的最小值
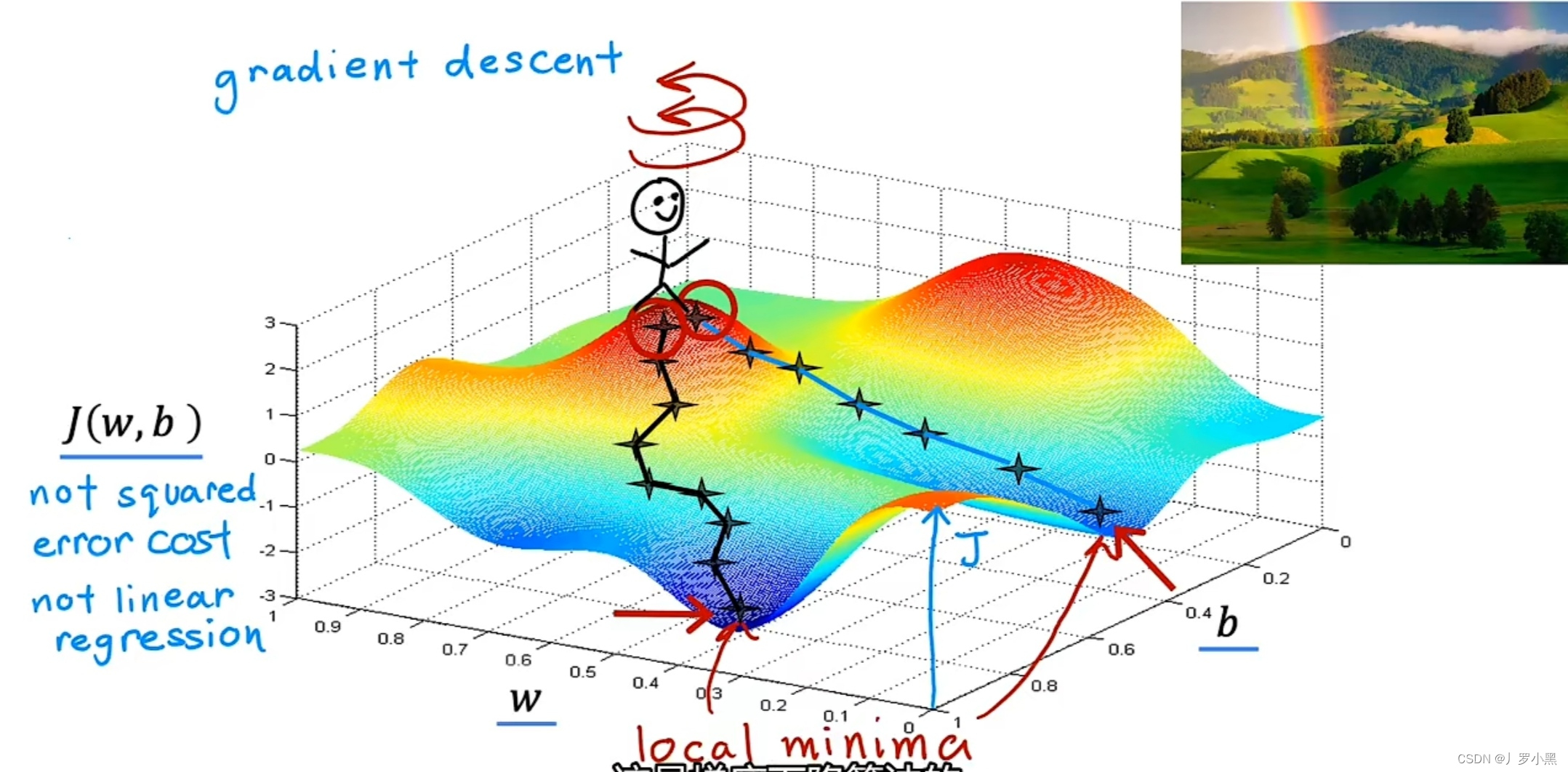
- 例如:深度学习模型的成本函数
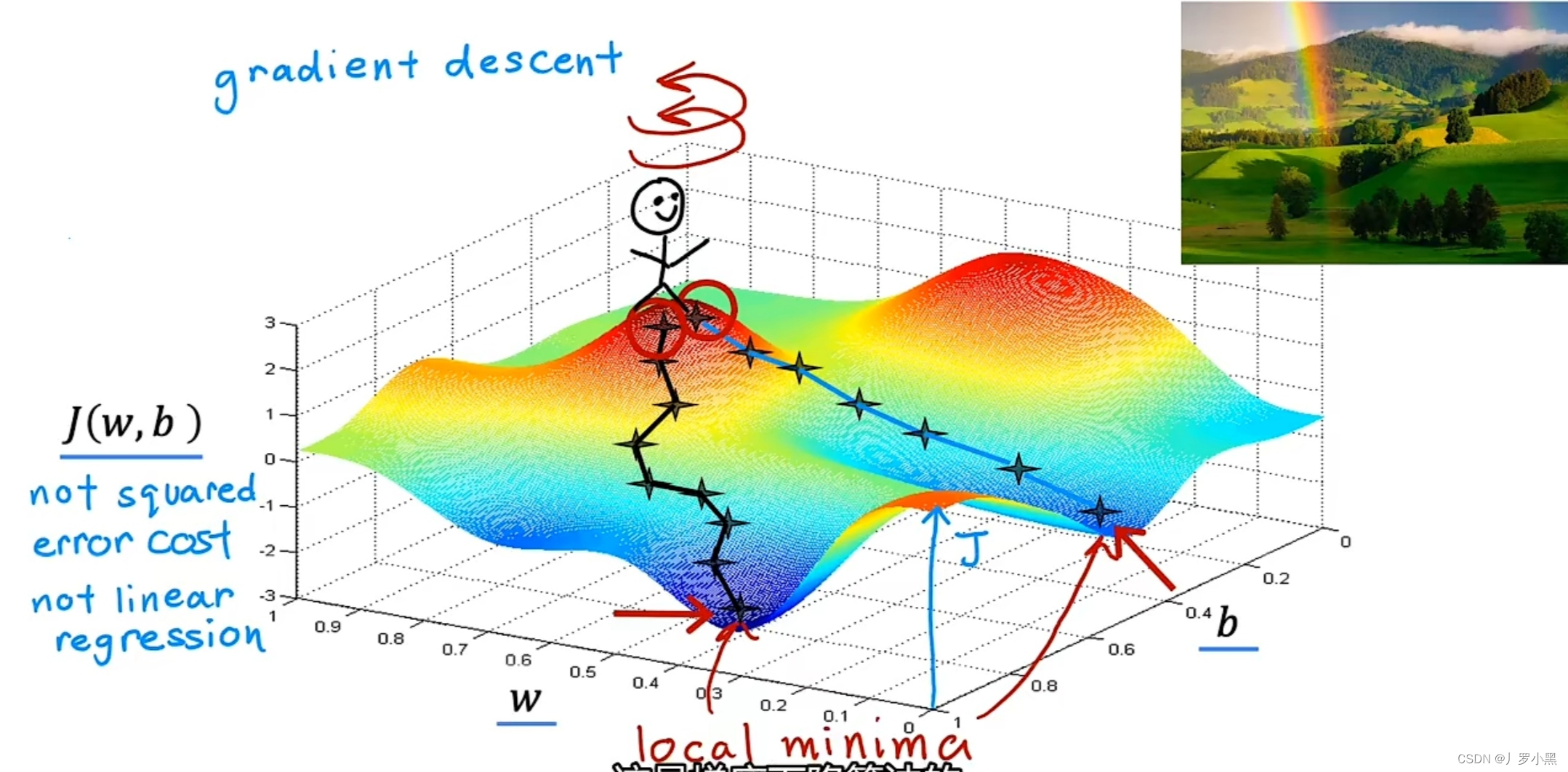
- 梯度下降算法形象化的步骤:
a. 选取一组w和b作为初始位置
b. 站在初始位置上,旋转360°,找到一个最高效下到这些山谷之一的底部的方向,并迈出一小步。从数学上来讲,这个方向是最陡下降方向
c. 站在迈出一小步后的位置上,并重复上一步的过程
d. 站在下一个位置上,重复上一步的过程
…
e. 直到发现自己站在山谷的底部,而这个J函数的局部最小值就在这
- 梯度下降算法

- 梯度下降函数中有两个关键点:学习率和偏导数
- α:学习率,通常是介于0和1之间的一个很小的正数,如0.001。它控制下坡时迈多大的步子
- ∂J(w,b)/∂w 和 ∂J(w,b)/∂b:成本函数J对w求偏导,成本函数J对b求偏导。它控制下坡时朝哪个方向迈步子
- 梯度下降算法的步骤:
a. 更新w的值为,w - α × ∂J(w,b)/∂w
b. 更新b的值为,b - α × ∂J(w,b)/∂b
c. 重复更新w和b的值,直到w和b不随着继续更新而发生很大的变化,即偏导数趋于0,J函数趋于局部最小值,算法收敛 - 左边的方法是,在程序中正确的,同时更新两个参数的方法,因为他更新完w的值后,没有立即覆盖w,而是继续用旧w来更新b的值
- 右边的方法是,错误的,非同时更新两个参数的方法,因为他更新完w的值后,立即覆盖w,转而用新w来更新b的值
- 建议使用左边的正确的,同时更新两个参数的方法
- 梯度下降算法中的偏导数
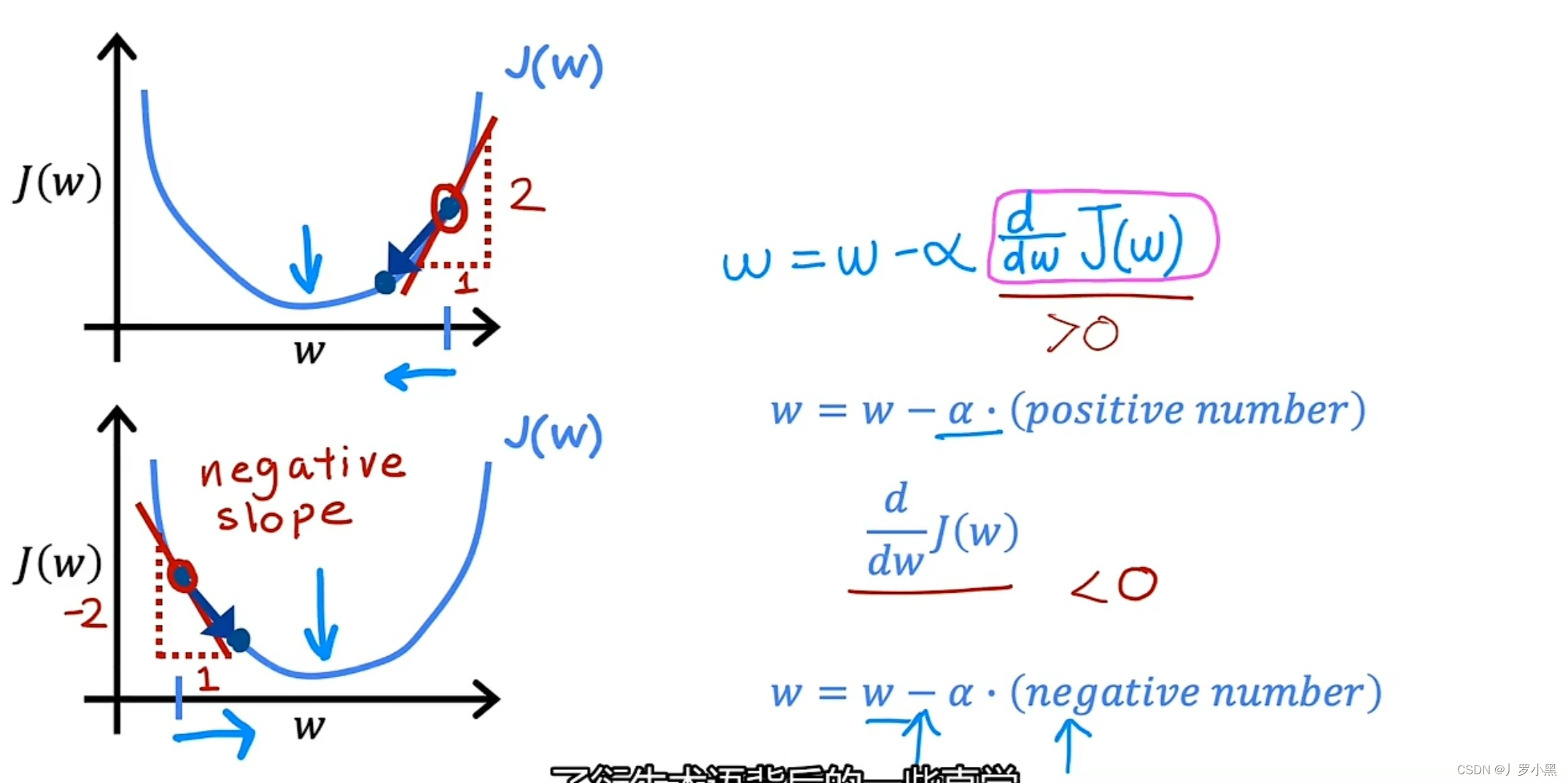
- 为了简化理解,我们将b设为0,J函数就变成一元函数,偏导数也就变成导数,我们可以用二维图来演示
- 导数的作用是在确定w的初始值后,决定w的变化方向,即确保J函数的值是在往J函数的局部最小值移动
- J函数上某点的导数为J函数在该点上的切线斜率。当w初始值在J函数最小值的右侧,切线斜率为正,该点导数为正,w减正数,w减小,即J函数值向局部最小值移动。当w初始值在J函数最小值的左侧,切线斜率为负,该点导数为负,w减负数为w加正数,w增加,即J函数值向局部最小值移动
- 梯度下降算法中的学习率
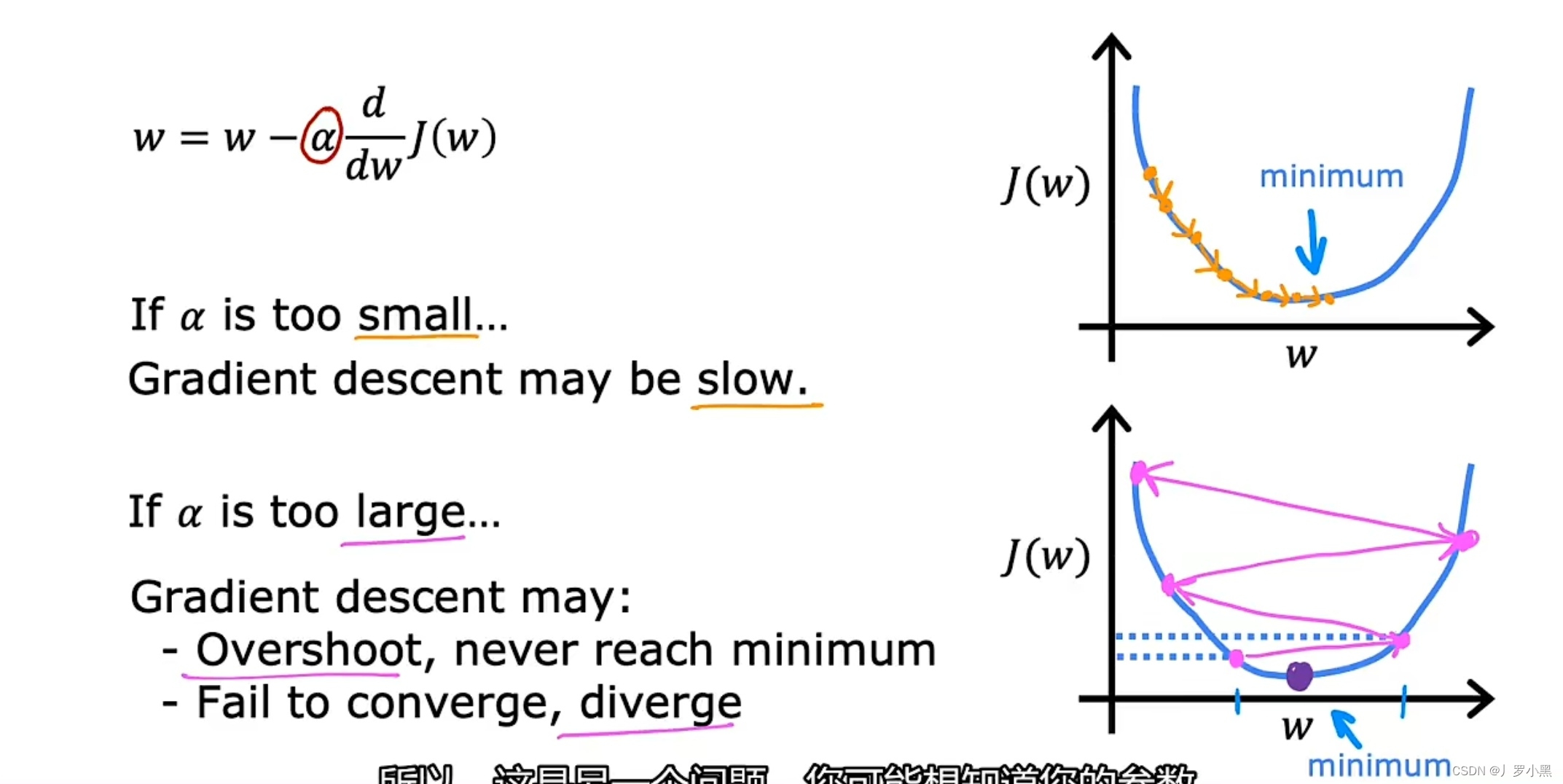
- 当学习率α过小时,梯度下降算法会执行的很慢,即要许多步才能到达J函数的局部最小值
- 当学习率α过大时,梯度下降算法每一步都会迈的很大。在这个例子中,当下一步的w超过了,前一步w关于J函数局部最小值的对称点时,J函数就会持续增大,那么该算法就达不到J函数的局部最小值,即算法不会收敛,反而会发散。
- 梯度下降算法的特性
- 当我们更改w和b的初始值后,会得到一个不同的局部最小值,如图:
- 当w到达某点,使J函数取局部最小值时,导数为0,梯度下降算法会保持w的值,不会让他继续改变,如图:

- 即使学习率固定,梯度下降算法也能让J函数到达局部最小值,如图:
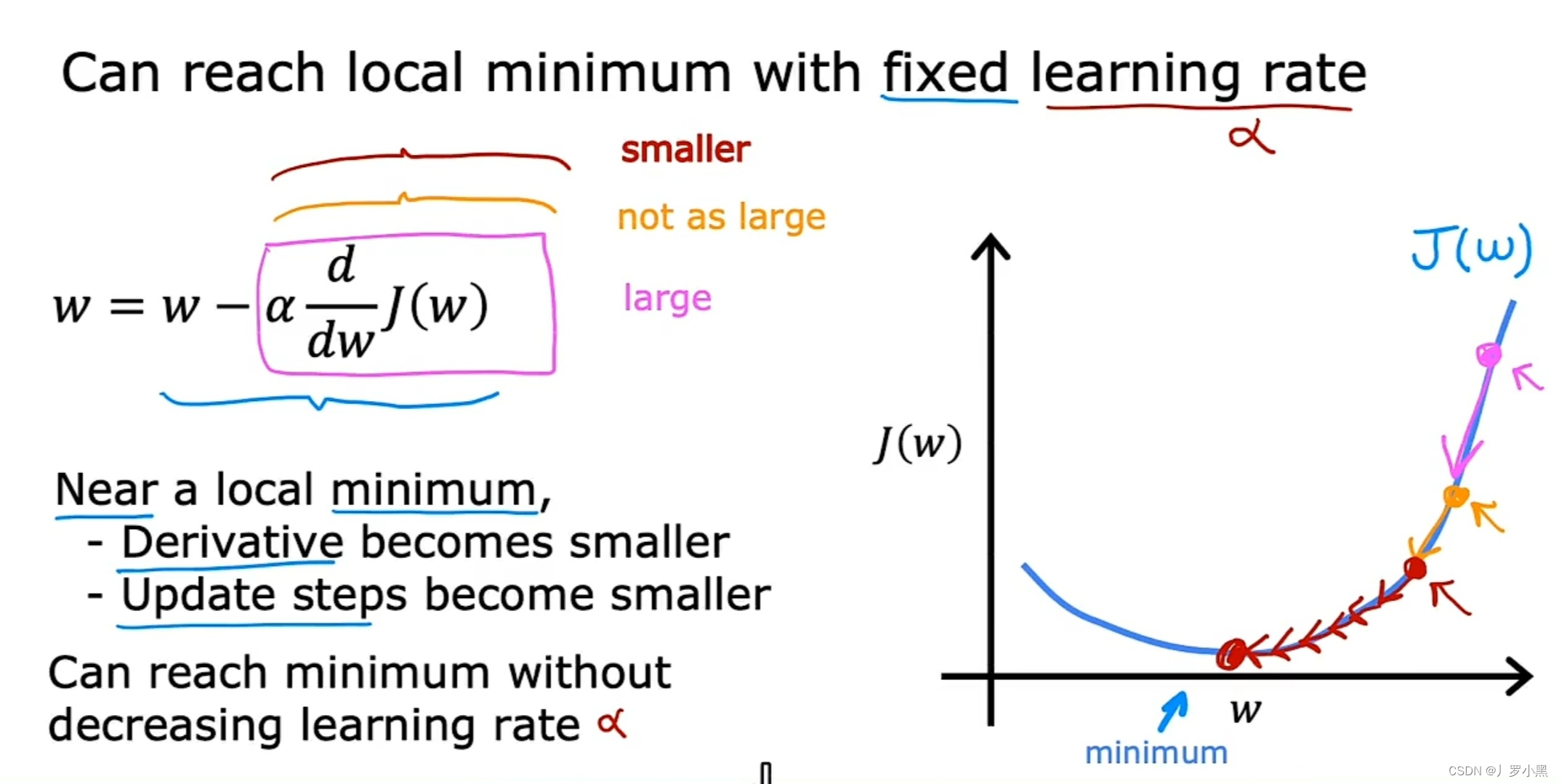
- 越靠近J函数的局部最小值,导数就越小,下一步迈的就越小,w值的变化就越小
- 用于线性回归的梯度下降算法

- 注意:f w,b (xⁱ) = w × xⁱ + b 是线性回归模型,且在每一步要同时更新w和b的值
- 简化公式的过程,如图:
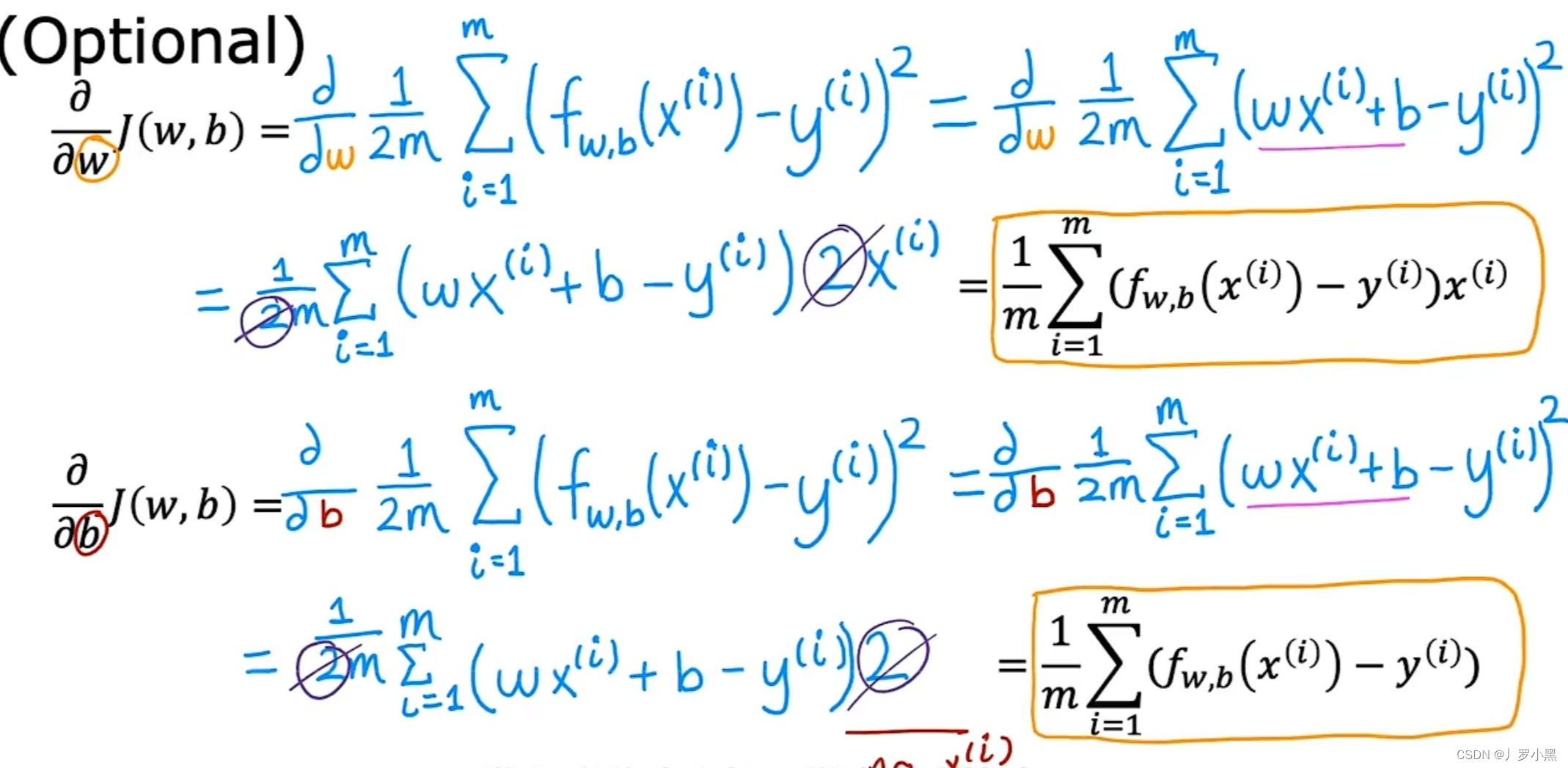
- 成本函数是非凸函数时,J函数会有多个局部最小值。例如深度学习模型的成本函数,如图:
- 成本函数是凸函数时,J函数具有碗型功能,且只有一个全局最小值,除此之外没有其他局部最小值。例如线性回归的平方误差成本函数,如图: