漫画：什么是快速排序算法？

news2024/10/5 19:16:44

这篇文章，以对话的方式，详细着讲解了快速排序以及排序排序的一些优化。

在这里插入图片描述

一禅：归并排序是一种基于分治思想的排序，处理的时候可以采取递归的方式来处理子问题。我弄个例子吧，好理解点。例如对于这个数组arr[] = { 4，1，3，2，7，5，8，0}。

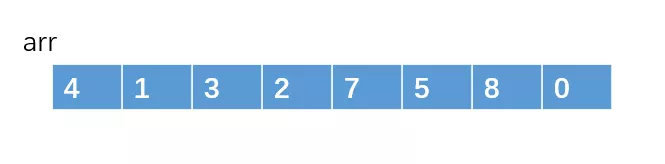
我们把它切割成两部分。

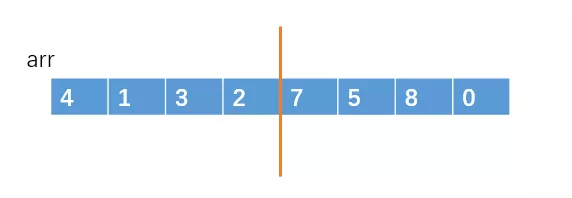
在这里插入图片描述
把左半部分和右半部分分别排序好。

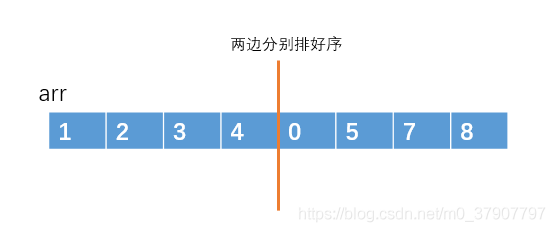
在这里插入图片描述
之后再用一个临时数组，把这两个有序的子数组汇总成一个有序的大数组

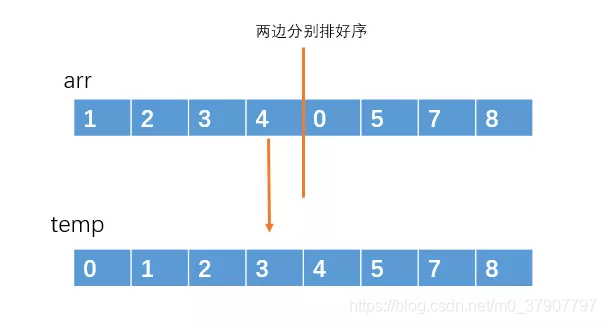
排好之后在复制原源arr数组

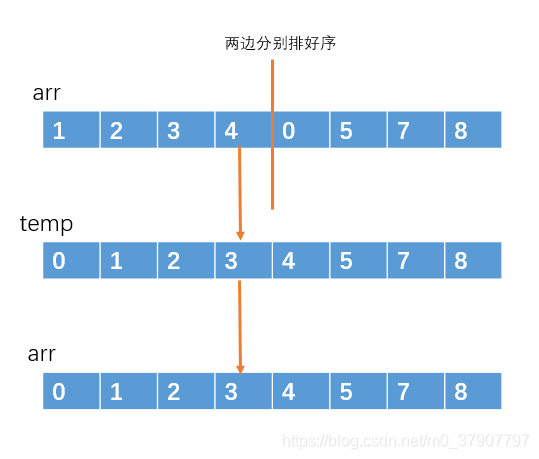
这时，源数组就排序完毕了

在这里插入图片描述

一禅：左半部分和右半部分的排序相当于一个原问题的一个子问题的，也是采取同样的方式，把左半部分分成两部分，然后…

直到分割子数组只有一个元素或0个元素时，这时子数组就是有序的了(因为只有一个元素或0个，肯定是有序的啊)，就不用再分割了，直接返回就可以了(当然，我在讲解这个归并排序的过程中，是假设你大致了解归并排序的前提下的了)

在这里插入图片描述

一禅：把一个n个元素的数组分割成只有一个元素的数组，那么我需要切logn次，每次把两个有序的子数组汇总成一个大的有序数组，所需的时间复杂度为O(n)。所以总的时间复杂度为O(nlogn)

快速排序

在这里插入图片描述

小白：那倒不是，快速排序的平均时间复杂度也是O(nlogn)，不过他不需要像归并排序那样，还需要一个临时的数组来辅助排序，这可以节省掉一些空间的消耗，而且他不像归并排序那样，把两部分有序子数组汇总到临时数组之后，还得在复制回源数组，这也可以节省掉很多时间。

在这里插入图片描述

小白：快速排序也是和归并排序差不多，基于分治的思想以及采取递归的方式来处理子问题。例如对于一个待排序的源数组arr = { 4，1，3，2，7，6，8}。

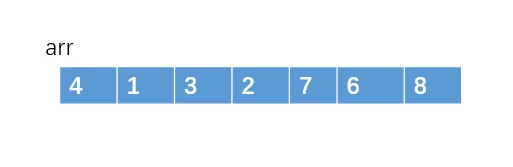
在这里插入图片描述
我们可以随便选一个元素，假如我们选数组的第一个元素吧，我们把这个元素称之为”主元“吧。

然后将大于或等于主元的元素放在右边，把小于或等于主元的元素放在左边。

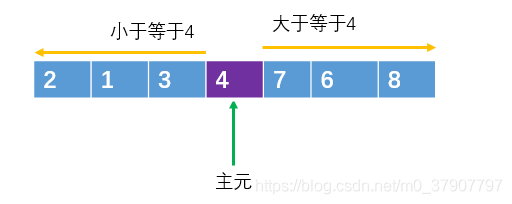
通过这种规则的调整之后，左边的元素都小于或等于主元，右边的元素都大于或等于主元，很显然，此时主元所处的位置，是一个有序的位置,即主元已经处于排好序的位置了。

主元把数组分成了两半部分。把一个大的数组通过主元分割成两小部分的这个操作，我们也称之为分割操作(partition)。

接下来，我们通过递归的方式，对左右两部分采取同样的方式，每次选取一个主元元素，使他处于有序的位置。
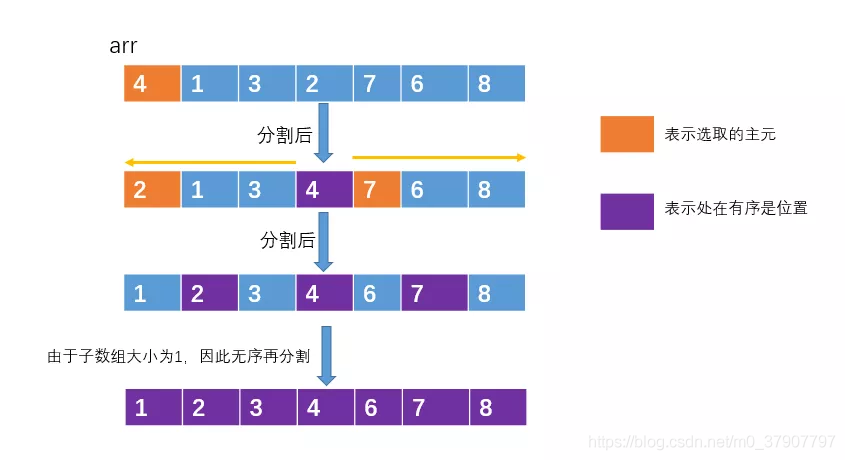
在这里插入图片描述

那什么时候递归结束呢？当然是递归到子数组只有一个元素或者0个元素了
在这里插入图片描述

分割操作：单向调整

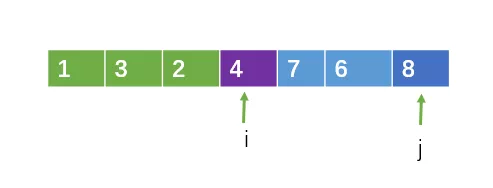
一禅：就按照你说的，选一个主元，你刚才选的是第一个元素为主元，这次我选最后一个为主元吧，哈哈。假设数组arr的范围为[left, right]，即起始下标为left，末尾下标为right。源数组如下
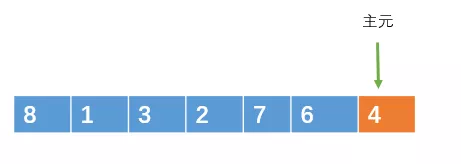
在这里插入图片描述
然后可以用一个下标 i 指向 left，即 i = left ;用一个下标 j 也指向l eft，即j = left

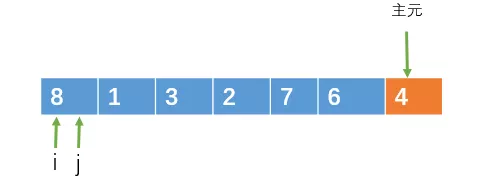
接下来 j 从左向右遍历，遍历的范围为 [left, right-1] ，遍历的过程中，如果遇到比主元小的元素，则把该元素与 i 指向的元素交换，并且 i = i +1
在这里插入图片描述
当j指向1时，1比4小，此时把i和j指向的元素交换，之后 i++。

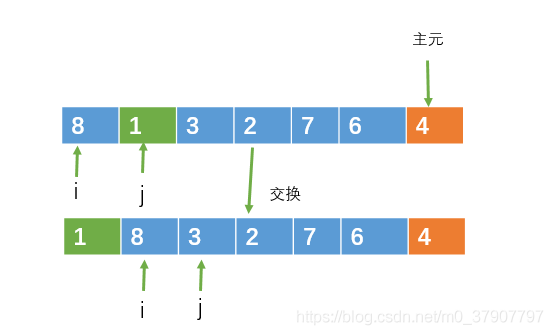
就这样让j一直向右遍历，直到 j = right

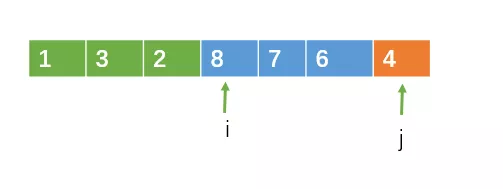
遍历完成之后，把 i 指向的元素与主元进行交换，交换之后，i 左边的元素一定小于主元，而 i 右边的元素一定大于或等于主元。这样，就 i 完成了一次分割了。
在这里插入图片描述

一禅一言不合就把代码撸好了，第一版代码如下：

//分割操作：方法一，单向调整
int partion(int a[], int left, int right)
{
   int temp,pivot;//pivot存放主元
   int i,j;
   i = left;
   pivot = a[right];
   for(j = left;j < right;j++)
   {
       if(a[j] < pivot)
       {  //交换值
           temp = a[i];
           a[i] = a[j];
           a[j] = temp;
           i++;
       }
   }
   a[right] = a[i];
   a[i] = pivot;
   return i;//把主元的下标返回
}
//快速排序
void QuickSort(int a[], int left, int right)
{
   int center;
   int i,j;
   int temp;
   if(left < right)
   {
      center = partion(a,left,right);
      QuickSort(a,left,center-1);//左半部分
      QuickSort(a,center+1,right);//右半部分
   }
}

分割操作：双向调整

在这里插入图片描述

小白：对啊，因为你这调整方法，可能会出现对同一个元素，进行多次交换，例如刚才你在演示的那组元素，在j向右遍历交换的过程中：

第一次：8和1交换

第二次：8和3交换

第三次：8和2交换

8被重复交换了很多次
在这里插入图片描述

小白：其实，我们可以这样来调整元素。我还是用我的第一个元素充当主元吧。哈哈

源数组如下
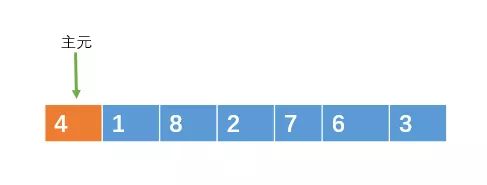
在这里插入图片描述
然后用令变量i = left + 1，j = right。然后让 i 和 j 从数组的两边向中间扫描。

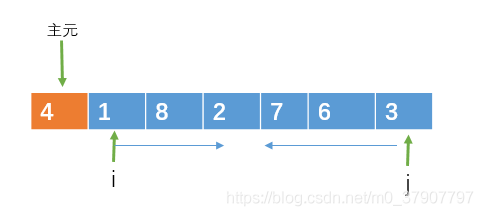
i 向右遍历的过程中，如果遇到大于或等于主元的元素时，则停止移动，j向左遍历的过程中，如果遇到小于或等于主元的元素则停止移动。
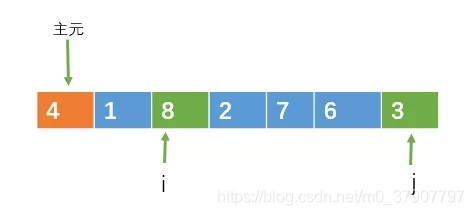
在这里插入图片描述
当i和j都停止移动时，如果这时i < j，则交换 i, j 所指向的元素。此时 i < j，交换8和3

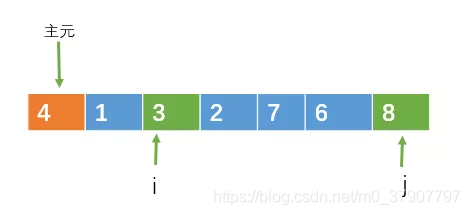
然后继续向中间遍历，直到i >= j。

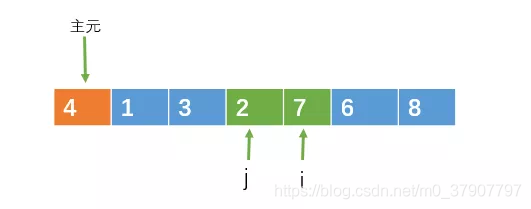
此时i >= j，分割结束。

最后在把主元与 j 指向的元素交换(当然，与i指向的交换也行)。
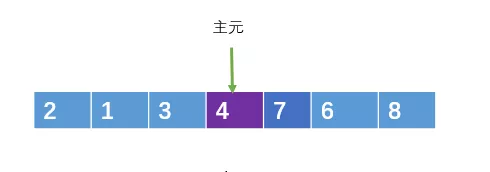
在这里插入图片描述
这个时候，j 左边的元素一定小于或等于主元，而右边则大于或等于主元。

到此，分割调整完毕

代码如下：

方法二：双向扫描
int partition2( int[] arr, int left, int right)
{
 int pivot = arr[left];
 int i = left + 1;
 int j = right;
 while(true)
 {  
   //向右遍历扫描
   while(i <= j && arr[i] <= pivot) i++;
   //向左遍历扫描
   while(i <= j && arr[j] => pivot) j--;
   if(i >= j)
     break;
   //交换
   int temp = arr[i];
   arr[i] = arr[j];
   arr[j] = temp;
 }
 //把arr[j]和主元交换
 arr[left] = arr[j];
 arr[j] = povit;
 return j;
}

时间复杂度

在这里插入图片描述

小白：因为快速排序的最坏时间复杂度是O(n2)。

例如有可能会出现一种极端的情况，每次分割的时候，主元左边的元素个数都为0，而右边都为n-1个。这个时候，就需要分割n次了。而每次分割整理的时间复杂度为O(n)，所以最坏的时间复杂度为O(n2)。

而最好的情况就是每次分割都能够从数组的中间分割了，这样分割logn次就行了，此时的时间复杂度为O(nlogn)。

而平均时间复杂度，则是假设每次主元等概率着落在数组的任意位置，最后算出来的时间复杂度为O(nlogn)，至于具体的计算过程，我就不展开了。

不过显然，像那种极端的情况是极少发生的。
在这里插入图片描述

小白：哈哈，之所以说它快，是因为它不像归并排序那样，需要额外的辅助空间，而且在分割调整的时候，不像归并排序那样，元素还要在辅助数组与源数组之间来回复制。

稳定性

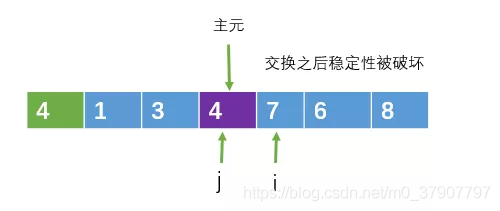
在这里插入图片描述

一禅：不是啊，例如，在排序的过程中，主元在和j交换的时候是有可能破坏稳定性的，例如

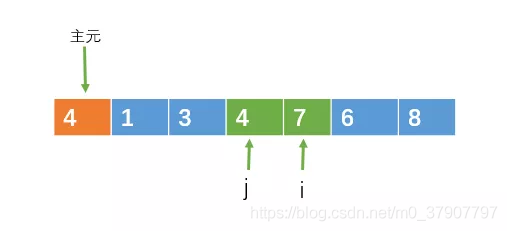
把主元与j指向的元素进行交换

//随机选取主元
int random_partition(int[] arr, int left, int right)
{
 i = random(left, right);//随机选取一个位置
 //在把这个位置的元素与ar[left]交换
 swap(arr[i], arr[left]);
 
 return partition(arr, left, right);
}