9.2 n元关系及其应用

n元关系：两个以上集合的元素间的关系

1、n元关系，关系的域，关系的阶

设A₁，A₂，……，A_n 是集合。定义在这些集合上的n元关系是A1×A2×……×An 的子集。这些集合A₁，A₂，……，A_n 称为关系的域，n称为关系的阶。

📘例1：设R是N × N × N上的三元组（a, b, c）构成的关系，是个3阶关系，其中a, b, c是满足a<b<c的整数。那么（1，2，3）∈ R，但是（2，4，3）∉R。它所有的域都等于自然数集。

📘例2：设 R 是 Z × Z × Z 上的三元组（a, b, c）构成的关系，是个3阶关系，其中a, b, c 构成等差数列，即（a，b，c）∈R iff 存在一个整数k，使得 b=a + k , c = a + 2k , 或者 b-a = k, c – b = k 。注意（1,3,5）∈R，但是（2,5,9）∉R,且它所有的域都等于整数集。

//iff：if and only if，当且仅当

2、数据库和关系

1. 数据库

数据库由记录组成，这些记录是由域构成的n元组。
这些域是n元组的数据项

用于表示数据库的关系也称为表（因为这些关系常常用表来表示）。表中每个列对应数据库的一个属性

📘例：
表1是学生数据库。这个数据库的属性有学生姓名、学号、专业和GPA

2. 主键

当n元组的某个域的值能够确定这个n元组时，n元关系的这个域就叫作主键。

这就是说，当关系中没有两个n元组在这个域有相同的值时，这个域就是主键。

❗ 主键可以有不止一个

主键的选择要考虑历史因素！！！考虑数据库的内涵

3. 复合主键

在一个n元关系中，域的组合也可以唯一地标识n元组。当一组域的值确定一个关系中的n元组时，这些域的笛卡儿积就叫作 复合主键

3、n元关系的运算

1. 选择运算 (Select)

设R是一个 n 元关系，C是关系R中元素可能满足的一个条件。定义选择运算 S_c是 将 n 元关系R映射到R中满足条件C的所有n元组构成的n元关系。

⭕选择运算 S_c将 n 元关系R中的所有满足条件的C的行挑出来组成一个新的n元关系。相当于在原来的数据表中按照条件C选出了某些行构成一个子表。

📘例：在教学课程表中查看物理学专业同学的选课情况。

2. 投影运算 (Project)

投影P_i1,i2,…,im，其中i1<i2<……<im,将n元组（a₁,a₂,……,a_n）映射到m元组（a_i1,a_i2,……,a_im），其中m ≤ n 。

投影运算 P_i1,i2,…,im 删除了 n 元组中的n-m个分量，保留了第i1,i2,…,im个分量所有 满足投影条件的列挑出来组成一个新的n-m 元关系。相当于在原来的数据表中按照投影条件选出了某些列构成一个子表。

📘例：在教学安排表中查看教授出现在教室的时间地点。

📘例：

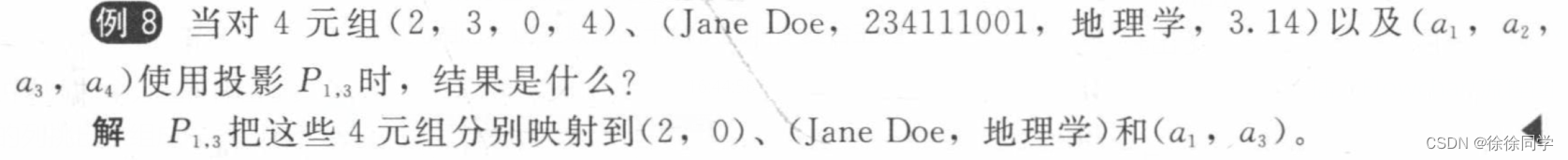
3. 连接运算

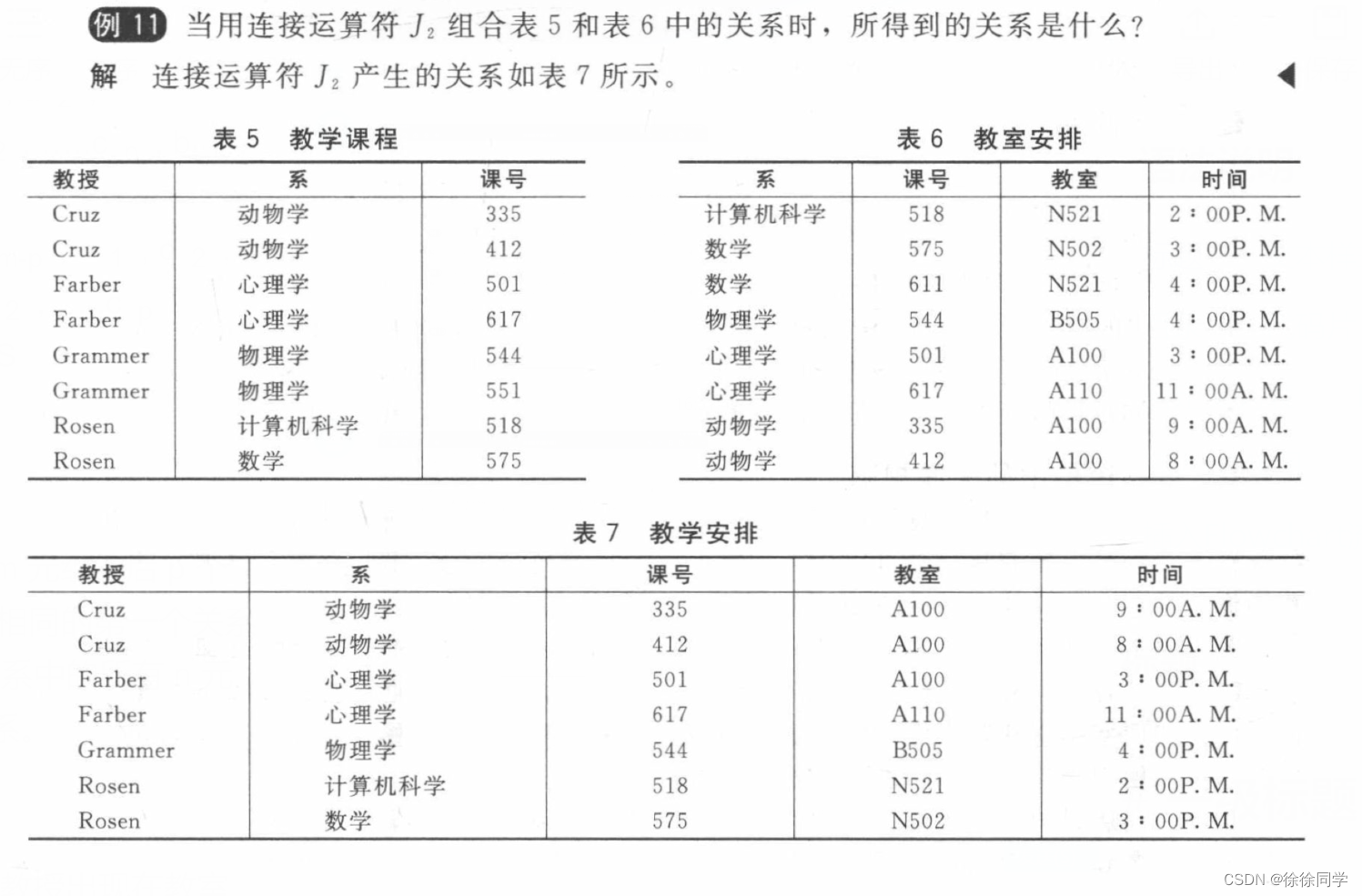
设R是m元关系，S是n元关系。定义连接运算 J_p(R,S) 是 m + n - p 元关系，其中 (p≤𝑚) ∧(𝑝 ≤𝑛) , 它包含了所有的 （m + n - p）元组 （a₁, a₂, a₃,……., a_m-p, c₁, c₂, ……c_p, b₁, b₂, ……, b_n-p）, 其中 ，
（a₁, a₂, a₃,……., a_m-p, c₁, c₂, ……c_p）∈R ∧ （c₁, c₂, ……c_p, b₁, b₂, ……, b_n-p） ∈S

即：连接运算 J_p(R,S) 将 m 元组的后 p 个分量与 n 元组的前 p 个分量相同的第一个关系中的所有 m 元组和第二个关系中的所有 n 元组组合起来形成一个新的关系。

通俗来说就是把两个表合并

📘例：