0102加权quick_union和路径压缩-union-find-动态连通性-算法研究

3 union-find算法

3.5 加权quick-union算法

3.5.1 算法实现

quick-union出现最坏情况，因为我们是随意将一棵树链接到另外一棵树上，修改如下：

添加一个数组和一些代码记录树中节点数；
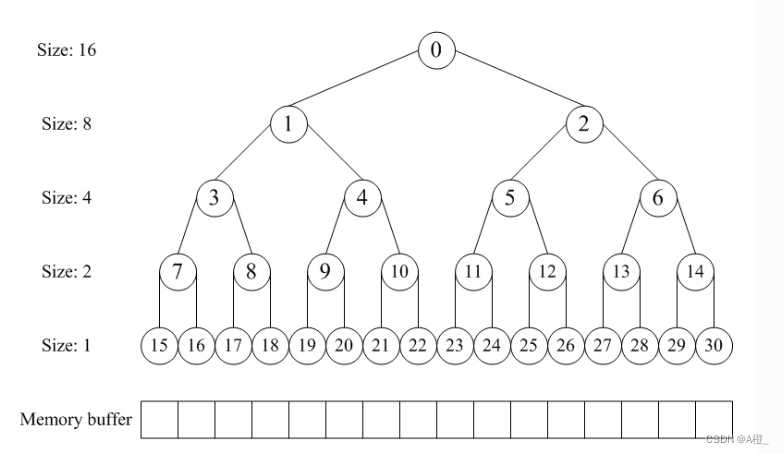
链接时将节点数较小的树链接到较大的树上，示意图3.5.1-1如下所示：

在这里插入图片描述

这样能大大改进算法的效率，我们将它称为加权quick-union算法。

基于union-find各实现算法的相同性，遵循依赖倒置原则，我们设计一个同一的接口，抽象相同的方法，一个抽象实现类，实现相同的方法。

UnionFind接口代码如下3.5.1所示：

package com.gaogzhen.algorithms4.foundation;

/**
 * union-find算法功能接口
 */
public interface UnionFind {

    /**
     * 查找触点p所在分量标志
     * @param p 触点p
     * @return 分量标志
     */
    int find(int p);

    /**
     * 触点p和触点q是否在同一分量内
     * @param p 触点p
     * @param q 触点q
     * @return {@code true}如果触点{@code p}和触点{@code q}在同一分量内；{@code false}否则
     */
    boolean connected(int p, int q);

    /**
     * 合并触点p和触点q
     * @param p 触点q
     * @param q 触点q
     */
    void union(int p, int q);


    /**
     * 分量数量
     * @return 分量数量
     */
    int count();
}

抽象类AbstractUnionFind代码3.5-2如下所示（有待进一步完善）：

package com.gaogzhen.algorithms4.foundation;

/**
 * union-find 默认实现
 */
public abstract class AbstractUnionFind implements UnionFind{

    /**
     * 触点所在分量标志
     */
    private int[] id;

    /**
     * 连通分量数量
     */
    private int count;


    /**
     * 初始化数组id
     * @param n 数组长度
     */
    public AbstractUnionFind(int n) {
        count = n;
        id = new int[n];
        for (int i = 0; i < n; i++)
            id[i] = i;
    }


    /**
     * 获取触点i对应的分量值
     * @param index 触点i
     * @return  触点对应的分量标志
     */
    protected int getId(int index) {
        return id[index];
    }

    /**
     * 设置触点i对应的分量值
     * @param index 触点index
     * @param val 分量值
     */
    protected void setId(int index, int val) {
        this.id[index] = val;
    }

    /**
     * 数组id长度
     * @return 数组id长度
     */
    protected int capacity() {
        return id.length;
    }


    /**
     * 分量数量减1
     */
    protected void decreaseCount() {
        count--;
    }

    /**
     * 连通分量的数量
     *
     * @return 数量 (between {@code 1} and {@code n})
     */
    @Override
    public int count() {
        return count;
    }

    /**
     * 校验触点p是否合法
     * @param  p 触点p
     */

    protected void validate(int p) {
        int n = id.length;
        if (p < 0 || p >= n) {
            throw new IllegalArgumentException("index " + p + " is not between 0 and " + (n-1));
        }
    }

    /**
     * 判断触点p和触点q是否相连
     *
     * @param  p 触点p
     * @param  q 触点q
     * @return {@code true} 如果 {@code p} 和 {@code q} 相连;
     *         {@code false} 否则
     */
    @Deprecated
    @Override
    public boolean connected(int p, int q) {
        validate(p);
        validate(q);
        return find(p) == find(q);
    }
}

加权qucik-union算法实现代码如下3.5-3所示：

package com.gaogzhen.algorithms4.foundation;

/**
 *  加权quick-union
 */
public class WeightedQuickUnionUF extends AbstractUnionFind{

    /**
     * 当前触点为根节点树中节点数量
     */
    private int[] size;


    /**
     * 初始化n个触点的数组
     *
     * @param  n 数量n
     */
    public WeightedQuickUnionUF(int n) {
        super(n);
        size = new int[n];
        for (int i = 0; i < n; i++) {
            size[i] = 1;
        }
    }



    /**
     * 返回触点p所在分量标志
     *
     * @param  p 触点p
     * @return 触点p所在分量标志
     */
    public int find(int p) {
        validate(p);
        while (p != getId(p))
            p = getId(p);
        return p;
    }

    /**
     * 合并触点p和触点q所在的分量
     *
     * @param  p 触点p所在分量
     * @param  q 触点p所在分量
     */
    public void union(int p, int q) {
        int rootP = find(p);
        int rootQ = find(q);
        if (rootP == rootQ) return;

        // make smaller root point to larger one
        if (size[rootP] < size[rootQ]) {
            setId(rootP, rootQ);
            size[rootQ] += size[rootP];
        }
        else {
            setId(rootQ, rootP);
            size[rootP] += size[rootQ];
        }
        decreaseCount();
    }
}

测试代码做相应调整3.5-4如下所示：

public static void testWeightedUF() {
    In in = fetchData();
    int n = in.readInt();
    testUF(new WeightedQuickUnionUF(n), in);
}

private static In fetchData() {
    String path = System.getProperty("user.dir") + File.separator + "asserts/tinyUF.txt";
    return new In(path);
}

private static void testUF(UnionFind uf, In in) {
    while (!in.isEmpty()) {
        int p = in.readInt();
        int q = in.readInt();
        if (uf.find(p) == uf.find(q)) continue;
        uf.union(p, q);
        StdOut.println(p + " " + q);
    }
    StdOut.println(uf.count() + " components");
}

测试结果如下所示；

4 3
3 8
6 5
9 4
2 1
5 0
7 2
6 1
2 components

3.5.2 算法性能分析

命题H。对于N个触点，加权quick-union算法构造的森林中的任意节点的深度最多为 $\lg N$ 。

证明：数学归纳法证明一个更强的命题，即森林中大小为k的树的高度最大为 $\lg k$ 。

$证明：当k的高度为1时，树的高度为0\\ 根据归纳法，假设大小为i的树的高度最多为\lg i,i\le k\\ 设i\le j且i+j=看，当我们将大小为i和大小为j的树归并时，小树的高度+1，即\\ i+\lg i=\lg(2i)\le\lg(i+j)=\lg k$

推论。对于加权quick-union算法和N个触点，在最坏情况下find()、connected()和union()的成本低增长数量级为 $\lg N$ 。

证明。在森林中，对于从一个节点到它根节点到路径上的每个节点，每种操作最多都只会访问数组常数次。

加权quick-union算法处理N个触点和M条连接时最多访问数组 $cM\lg N次，c为常数$ 。而quick-find则至少需要访问NM次。因此，加权quick-unino算法能让我们在合理的时间内解决实际中大规模动态连通性问题。

3.6 路径压缩

理想情况下，我们希望每个节点都直接链接到它的根节点上。

路径压缩算法其中一种实现代码3.6-1如下所示：

package com.gaogzhen.algorithms4.foundation;


/**
 *
 */

public class UF extends AbstractUnionFind{

    /**
     * 触点为根节点树高度
     */
    private byte[] rank;


    /**
     * 初始化
     *
     * @param  n 数量
     */
    public UF(int n) {
        super(n);
        rank = new byte[n];
        for (int i = 0; i < n; i++) {
            rank[i] = 0;
        }
    }

    /**
     * 返回触点p所在分量的树的根节点
     *
     * @param  p 节点p
     * @return 节点p所在树根节点
     */
    public int find(int p) {
        validate(p);
        while (p != getId(p)) {
            // 路径减半压缩，当前节点指向其祖父节点
            setId(p , getId(getId(p)));
            p =  getId(p);
        }
        return p;
    }
    /**
     * 归并触点p和触点q
     *
     * @param  p 触点p
     * @param  q 触点q
     */
    public void union(int p, int q) {
        int rootP = find(p);
        int rootQ = find(q);
        if (rootP == rootQ) return;

        // 较低高度的树链接到较高高度的树
        if      (rank[rootP] < rank[rootQ]) setId(rootP, rootQ);
        else if (rank[rootP] > rank[rootQ]) setId(rootQ, rootP);
        else {
            // 高度相同，一个链接到另外一个，被链接的高度+1
            setId(rootQ, rootP);
            rank[rootP]++;
        }
        decreaseCount();
    }
}

find()方法：通过循环，将路径上遇到的所有节点直接链接到根节点；

测试代码3.6-2如下所示：

public static void testPathCompress() {
    In in = fetchData();
    int n = in.readInt();
    testUF(new UF(n), in);
}

fetchData()和testUF()代码同上，测试结果：

4 3
3 8
6 5
9 4
2 1
5 0
7 2
6 1
2 components

3.7 分析

路径压缩的加权quick-union算是目前最优的算法，但并非所有操作都能在常数时间内完成。使用路径压缩的加权quick-union算法的每个操作在最坏情况下（均摊后）都不是常数级别。

各种union-find算法上性能特点如下表3.7-1所示：

算法	N 个触点时成本增长数量级（最坏情况下）
	构造函数	union()	find()
quick-find	N	N	1
quick-union	N	树的高度	树的高度
加权quick-union	N	$\lg N$	$\lg N$
路径压缩加权quick-union	N	接近1	均摊成本
理想情况	N	1	1