一、 题目

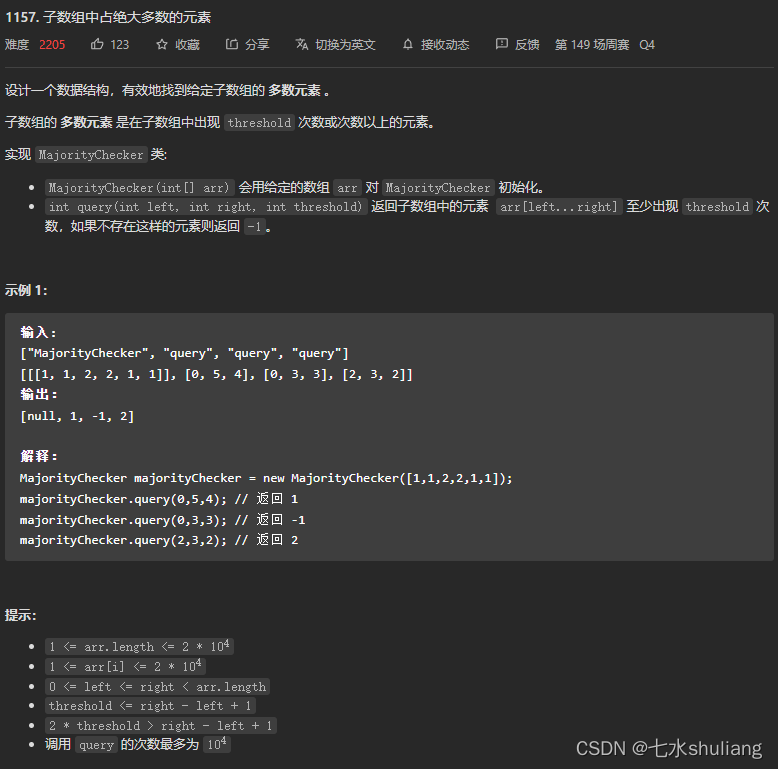
1. 题目描述

2. 原题链接

链接: 1157. 子数组中占绝大多数的元素

二、 解题报告

1. 思路分析

 这题之前写过，用线段树维护区间内最多两个元素和数量，数据过了，但其实是错的，被蛙佬hack了。
 原因是会最多那个元素的数量必会丢失，那么threshold设置到区间内那个主元素数量，就会返回-1了。

[已被hack]线段树维护区间内前两多的元素数量，暴力合并区间。

["MajorityChecker", "query", "query"]
[[[2, 3, 1, 1, 1]], [0, 4, 3], [1, 3, 2]]

---

• 正解可以随机化算法，或者线段树+摩尔投票。

---

• 随机化比较好理解，如果区间内存在绝对众数的话，只会存在一个，那么随机取一个数，取到它的概率超过1/2。
  • 那我们取20次，每次判断它是否是绝对众数，是的话判断threshold返回即可；
    • 这个可以优化，如果是绝对众数，但不符合threshold，可以返回-1了，因为不会有其他绝对众数。
  • 如果20次都没取到，就认为没有绝对众数。成功率99%(1-0.5**20)。
• 如何判断一个数在区间内是否是绝对众数呢。
  • 预处理，按照数字分组，每组记录下标列表。
  • 查询[l,r]区间内的这个数字个数，只需要在对应的列表上二分。

---

• 方法二，摩尔投票+线段树。
• 线段树节点维护每个区间内最多的元素，以及它比其他数多多少个。（类似摩尔投票的x,cnt）
• 这个节点性质是可以两个线段合并的，具体见代码。
• 同摩尔投票，找到可能得绝对众数后，依然需要二分验证实际的数量。

2. 复杂度分析

最坏时间复杂度O(nlog₂n)

3. 代码实现

随机化。

class MajorityChecker:

    def __init__(self, arr: List[int]):
        self.pos = defaultdict(list)
        for i,v in enumerate(arr):
            self.pos[v].append(i)
        self.arr = arr

    def query(self, left: int, right: int, threshold: int) -> int:
        for i in range(20):
            x = self.arr[randint(left,right)]
            cnt = bisect_right(self.pos[x],right) - bisect_left(self.pos[x],left)
            if cnt >=threshold:
                return x
        return  -1

摩尔投票+二分

class IntervalTree:
    def __init__(self, size,nums=None):
        self.size = size
        self.nums = nums
        self.interval_tree = [(0,0) for _ in range(size*4)]
        if nums:
            self.build_tree(1,1,size)
    def sum_node(self,a,b):
        if a[0] == b[0]:
            return (a[0],a[1]+b[1])
        elif a[1]<b[1]:
            return (b[0],b[1]-a[1])
        else:
            return (a[0],a[1]-b[1])

    def build_tree(self,p,l,r):
        interval_tree = self.interval_tree
        nums = self.nums
        if l == r:
            interval_tree[p] = (nums[l-1],1)
            return
        mid = (l+r)//2
        self.build_tree(p*2,l,mid)
        self.build_tree(p*2+1,mid+1,r)
        interval_tree[p] = self.sum_node(interval_tree[p*2],interval_tree[p*2+1])
      
    def sum_interval(self,p,l,r,x,y):        
        if y < l or r < x:
            return 0
        interval_tree = self.interval_tree
        if x<=l and r<=y:
            return interval_tree[p]
        mid = (l+r)//2
        s = (-1,0)
        if x <= mid:
            s = self.sum_node(s,self.sum_interval(p*2,l,mid,x,y))
        if mid < y:
            s = self.sum_node(s,self.sum_interval(p*2+1,mid+1,r,x,y))                  
        return s
class MajorityChecker:

    def __init__(self, arr: List[int]):
        self.tree = IntervalTree(len(arr),arr)
        self.n = len(arr)
        self.pos = defaultdict(list)
        for i,v in enumerate(arr):
            self.pos[v].append(i)
        

    def query(self, left: int, right: int, threshold: int) -> int:
        ans,_ = self.tree.sum_interval(1,1,self.n,left+1,right+1)
        lst = self.pos[ans]
        cnt = bisect_right(lst,right) - bisect_left(lst,left)
        if cnt >= threshold:
            return ans 
        return  -1

三、 本题小结

四、 参考链接