题解
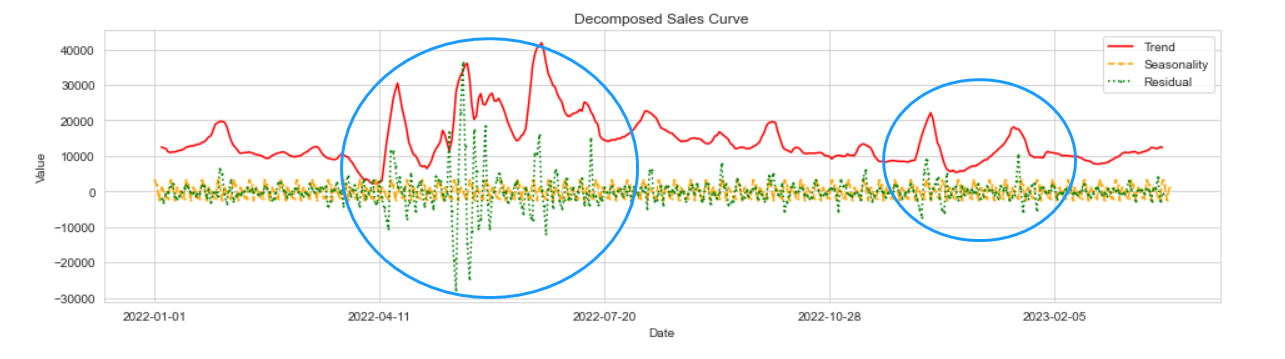
引入:tarjan算法,强连通分量,割点,割边,点双联通分量,边双联通分量
P4961 小埋与扫雷
思路:分别求出数字和空格相加即可
#include<iostream>
using namespace std;
const int X[8] = { -1,-1,-1,0,0,1,1,1 };
const int Y[8] = { -1,0,1,-1,1,-1,0,1 };
int dir[8][2]{ {-1,-1},{-1,0},{-1,1},{0,-1},{0,1},{1,-1},{1,0},{1,1} };
int a[1005][1005];
int n, m, ans;
void dfs(int x, int y){
a[x][y] = 3;
for (int i = 0; i < 8; i++) {
int tx = x + dir[i][0];
int ty = y + dir[i][1];
if (tx >= 1 && tx <= n && ty >= 1 && ty <= m) {
if (!a[tx][ty])
dfs(tx, ty);
}
}
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++){
for (int j = 1; j <= m; j++)
cin >> a[i][j];
}
for (int i = 1; i <= n; i++){
for (int j = 1; j <= m; j++){
if (!a[i][j])
for (int l = 0; l < 8; l++) {
int tx = i + dir[l][0];
int ty = j + dir[l][1];
if (a[tx][ty] == 1)
a[i][j] = 2;
}
}
}
for (int i = 1; i <= n; i++){
for (int j = 1; j <= m; j++){
if (a[i][j] == 2) {
int flag = 1;
for (int l = 0; l < 8; l++){
if (a[i + X[l]][j + Y[l]] == 0 && i + X[l] >= 1 && i + X[l] <= n && j + Y[l] >= 1 && j + Y[l] <= m)
flag = 0;
}
ans+=flag;
}
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++){
if (!a[i][j]){
ans++;
dfs(i, j);
}
}
}
cout << ans;
return 0;
}
洛谷P3388 【模板】割点(割顶)
给出一个 n 个点,m 条边的无向图,求图的割点。
如果 p 存在一个子结点 q 满足 low(q)≥dfsn(p) ,则p为割点
特殊情况,根节点需要有两个子节点才为割点
#include<iostream>
#include<vector>
#include<stack>
#include<cstring>
using namespace std;
const int MAXN = 1000000;
int dfsn[MAXN], low[MAXN];
vector<int>edges[MAXN];
bool cut[MAXN];
int sum = 0 , cnt;
void tarjan(int p, bool root = true)
{
int tot = 0;
low[p] = dfsn[p] = ++cnt;
for (auto q : edges[p])
{
if (!dfsn[q])
{
tarjan(q, false);
low[p] = min(low[p], low[q]);
tot += (low[q] >= dfsn[p]); // 统计满足low[q] >= dfsn[p]的子节点数目
}
else
low[p] = min(low[p], dfsn[q]);
}
if (tot > root) { // 如果是根,tot需要大于1;否则只需大于0
sum++;
cut[p] = true;
}
}
int main()
{
ios::sync_with_stdio(false);
int n, m;
cin >> n >> m;
for (int i = 0; i < m; i++) {
int a, b;
cin >> a >> b;
edges[a].push_back(b);
edges[b].push_back(a);
}
for (int i = 1; i <= n; ++i)
if (!dfsn[i])
tarjan(i);
cout << sum << '\n';
for (int i = 1; i <= n; i++) {
if (cut[i])
cout << i << ' ';
}
return 0;
}
洛谷P3387 【模板】缩点
思路:tarjan求出强连通分量,缩点建新图,之后拓扑序dp
#include<iostream>
#include<stack>
#include<algorithm>
#include<vector>
#include<queue>
#define int long long
const int MAXN = 1e5+10;
using namespace std;
vector<int> edges[MAXN];
vector<int> edges2[MAXN];
stack<int>stk;
int dfsn[MAXN], low[MAXN], instk[MAXN], scc[MAXN], cnt, cscc;
int ans;
int a[MAXN],w[MAXN],dis[MAXN];
int d[MAXN];
void tarjan(int p)
{
low[p] = dfsn[p] = ++cnt;
instk[p] = 1;
stk.push(p); // 进栈
for (auto q : edges[p])
{
if (!dfsn[q]) // 未访问过
{
tarjan(q); // 递归地搜索
low[p] = min(low[p], low[q]);
}
else if (instk[q]) // 访问过,且q可达p
low[p] = min(low[p], dfsn[q]);
}
if (low[p] == dfsn[p]) // 发现强连通分量的根
{
int top;
cscc++;
do
{
top = stk.top();
stk.pop();
instk[top] = 0;
scc[top] = cscc; // 记录所属的强连通分量
} while (top != p); // 直到弹出p才停止
}
}
signed main()
{
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++) {
cin >> a[i];
}
for (int i = 1; i <= m; i++) {
int a, b;
cin >> a >> b;
edges[a].push_back(b);
}
for (int i = 1; i <= n; ++i)
if (!dfsn[i])
tarjan(i);
for (int u = 1; u <= n; ++u) { //缩点
for (auto v : edges[u]) {
if (scc[u] != scc[v]) {
edges2[scc[u]].push_back(scc[v]);
d[scc[v]]++;
}
}
w[scc[u]] += a[u]; //记录值包括(强连通分量)
}
queue<int>q;
for (int i = 1; i <= cscc; i++) {
if (d[i] == 0) { //选择入度为0的点
dis[i] = w[i];
q.push(i);
}
}
while (q.size()) { //直到入度为0的点不存在
int u = q.front();
q.pop();
for (auto v : edges2[u]) {
dis[v] = max(dis[v], dis[u] + w[v]);
d[v]--; //删除与之相连的所有边,即入度-1
if (d[v] == 0) {
q.push(v);
}
}
}
for (int i = 1; i <= cnt; i++) { //比较以i为终点的最大值
ans = max(ans, dis[i]);
}
cout << ans << '\n';
return 0;
}
P1656 炸铁路
割桥模板题
如果 p 是 q 的父节点,并且low(q)>dfsn(p) ,那么 p<->q 是桥。
#include<iostream>
#include<cstring>
#include<vector>
#include<algorithm>
using namespace std;
const int MAXN = 5e3+10;
vector<int> bridges;
int dfsn[MAXN], low[MAXN], fa[MAXN], cnt;
vector<int>edges[MAXN];
int sum = 0,ans;
struct edge {
int u, v;
}e[MAXN];
bool cmp(edge x, edge y) {
if (x.u == y.u)
return x.v < y.v;
return x.u <y.u;
}
void tarjan(int p)
{
low[p] = dfsn[p] = ++cnt;
for (auto to : edges[p])
{
if (!dfsn[to])
{
fa[to] = p; // 记录父节点
tarjan(to);
low[p] = min(low[p], low[to]);
if (low[to] > dfsn[p]) {
e[ans].u = min(to,p);
e[ans].v = max(to, p);
ans++;
}
}
else if (fa[p] != to) // 排除父节点
low[p] = min(low[p], dfsn[to]);
}
}
int main()
{
ios::sync_with_stdio(false);
int n, m;
cin >> n >> m;
for (int i = 0; i < m; i++) {
int a, b;
cin >> a >> b;
edges[a].push_back(b);
edges[b].push_back(a);
}
for (int i = 1; i <= n; ++i)
if (!dfsn[i])
tarjan(i);
sort(e, e + ans, cmp);
for (int i = 0; i < ans; i++) {
cout << e[i].u << ' ' << e[i].v << '\n';
}
return 0;
}
P2863[USACO06JAN]The Cow Prom S
tarjan算法求出强连通分量,统计强连通分量>1的即可
#include<iostream>
#include<stack>
#include<algorithm>
#include<vector>
const int MAXN = 5e4+10;
using namespace std;
vector<int> edges[MAXN];
vector<int> edges2[MAXN];
stack<int>stk;
int dfsn[MAXN], low[MAXN], instk[MAXN], scc[MAXN], cnt, cscc;
int ans;
bool vis[MAXN];
int Cnt[MAXN];
void tarjan(int p)
{
low[p] = dfsn[p] = ++cnt;
instk[p] = 1;
stk.push(p); // 进栈
for (auto q : edges[p])
{
if (!dfsn[q]) // 未访问过
{
tarjan(q); // 递归地搜索
low[p] = min(low[p], low[q]);
}
else if (instk[q]) // 访问过,且q可达p
low[p] = min(low[p], dfsn[q]);
}
if (low[p] == dfsn[p]) // 发现强连通分量的根
{
int top;
cscc++;
do
{
top = stk.top();
stk.pop();
instk[top] = 0;
scc[top] = cscc; // 记录所属的强连通分量
} while (top != p); // 直到弹出p才停止
}
}
int main()
{
int n, m;
cin >> n >> m;
for (int i = 1; i <= m; i++) {
int a, b;
cin >> a >> b;
edges[a].push_back(b);
}
for (int i = 1; i <= n; ++i)
if (!dfsn[i])
tarjan(i);
for (int i = 1; i <= n; i++) {
Cnt[scc[i]]++;
if (Cnt[scc[i]] > 1 && !vis[scc[i]]) {
ans++;
vis[scc[i]] = 1;
}
}
cout << ans << '\n';
return 0;
}
P8435 【模板】点双连通分量
思路:寻找割点,特判根节点,根节点需要有两个子节点才为割点,弹栈直到割点为点,点双连通分量
#include <iostream>
#include<vector>
using namespace std;
const int maxn = 5e6 + 10;
int n, m, cut[maxn];
struct edge {
int to, nxt;
edge() {};
edge(int tto, int nnxt) {
to = tto;
nxt = nnxt;
}
}d[maxn]; int head[maxn], cnt = 1;
void add(int u, int v) { //链式前向星
d[++cnt] = edge(v, head[u]);
head[u] = cnt;
}
int low[maxn], dfn[maxn], stac[maxn], top, id, dc;
vector<int>dcc[maxn];
void tarjan(int u, int root)
{
dfn[u] = low[u] = ++id, stac[++top] = u;
if (u == root && !head[u])//孤立点
{
dcc[++dc].push_back(u);
return;
}
for (int i = head[u]; i; i = d[i].nxt)
{
int v = d[i].to;
if (!dfn[v]) // 未访问过
{
tarjan(v, root); // 递归地搜索
low[u] = min(low[u], low[v]);
if (low[v] >= dfn[u])//不通过u,v无法回到更浅的节点,割点
{
int temp; ++dc;//开始弹栈
//注意,如果u是父节点且只有1个儿子,不算割点,但也会开始弹栈
while (temp = stac[top--])
{
dcc[dc].push_back(temp);
if (temp == v) break;//直到遇到v
}
dcc[dc].push_back(u);
}
}
else
low[u] = min(low[u], dfn[v]);
}
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= m; i++)
{
int l, r; cin >> l >> r;
if (l == r)
continue;
add(l, r); add(r, l);
}
for (int i = 1; i <= n; i++)
if (!dfn[i]) tarjan(i, i);
cout << dc << '\n';
for (int i = 1; i <= dc; i++)
{
cout << dcc[i].size() << ' ';
for (int j = 0; j < dcc[i].size(); j++)
cout << dcc[i][j] << " ";
cout << '\n';
}
}
P8436 【模板】边双连通分量
思路:边联通分量即没有桥的连通分量,两个不同强连通分量不可达,
转变成求强连通分量
#include <iostream>
#include <cstring>
#include <vector>
using namespace std;
const int N = 5e5+10, M = (2e6+10) * 2;
int n, m;
int h[N], e[M], ne[M], idx;
int dfn[N], low[N], timestamp;
int stk[N], top;
int id[N], dcc_cnt;
int tot[N];
vector<int>dcc[M];
void add(int a, int b){
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
void tarjan(int u, int from){
dfn[u] = low[u] = ++timestamp;
stk[++top] = u;
for (int i = h[u]; ~i; i = ne[i]){
int j = e[i];
if (!dfn[j]){
tarjan(j, i);
low[u] = min(low[u], low[j]);
}
else if (i != (1 ^ from))
low[u] = min(low[u], dfn[j]);
}
if (dfn[u] == low[u])
{
dcc_cnt++;
int y;
do
{
y = stk[top--];
dcc[dcc_cnt].push_back(y);
} while (y != u);
}
return;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cin >> n >> m;
memset(h, -1, sizeof h);
for (int i = 1; i <= m; i++)
{
int a, b;
cin >> a >> b;
add(a, b);
add(b, a);
}
for (int i = 1; i <= n; i++)
if (!dfn[i]) tarjan(i, -1);
cout << dcc_cnt << endl;
for (int i = 1; i <= dcc_cnt; i++)
{
cout << dcc[i].size() << ' ';
for (int j = 0; j < dcc[i].size(); j++)
cout << dcc[i][j] << " ";
cout << '\n';
}
return 0;
}
git的使用()
版本迭代,版本管理器
1.版本控制
版本控制是指在软件开发过程中对各种程序代码、配置文件及说明文档等文件变更的管理,版本控制系统能够随着时间的推进记录一系列文件的变化,方便以后随时回退到某个版本。
多人开发
分类:
本地版本控制系统:个人
集中式版本控制系统 svn:协同工作的人们通过客户端连到中央服务器,需要联网,从服务器上拉取最新的代码,在本地开发,开发完成再提交到中央服务器。
分布式版本控制系统git:每个人拥有全部代码,安全隐患,不会因为服务器或网络造成不能工作
2.启动git
右键选项,任意文件夹
Git Bash:Unix与Linux风格的命令行
Git CMD:Windows风格命令行
Git GUI:图形界面的Git
3.常见的linux命令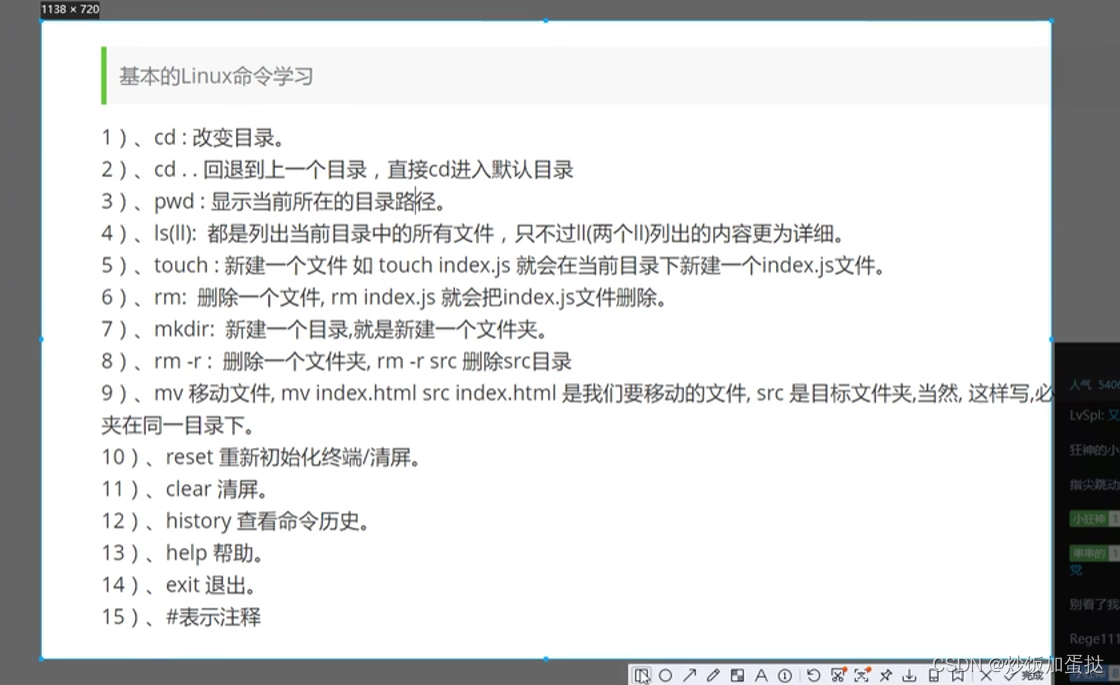
更多
gitee下的git大全和git命令学习
蓝色目录,绿色程序,白色程序
注:切勿rm -rf/ (格式化)
4.git的配置
查看配置 git config -l
查看系统配置 git config --system --list
查看本地配置 git config --global --list
注:用户名与密码必须配置
git的相关配置文件
所有的配置文件其实都保存在本地
D:\Git\Git\etc\gitconfig 系统级--system
C:\Users\abcd\.gitconflag 只适用当前登陆用户配置--global
设置用户与密码
git config --global user.name"用户"
5.git的工作原理(核心)
环境变量只是为了全局使用
Workspace:工作区 平时代码存放
Index/Stage:暂存区 临时存放改动,本质文件
Repository:仓库区 安全存放代码的地方 有提交的所有版本信息
Remote:远程仓库 托管代码的服务器
6.git工作的基本流程
1.工作目录添加,修改文件
2.需要进行版本管理的文件放入暂存区域
3.将暂存区域文件提交到git仓库
7.git的项目搭建
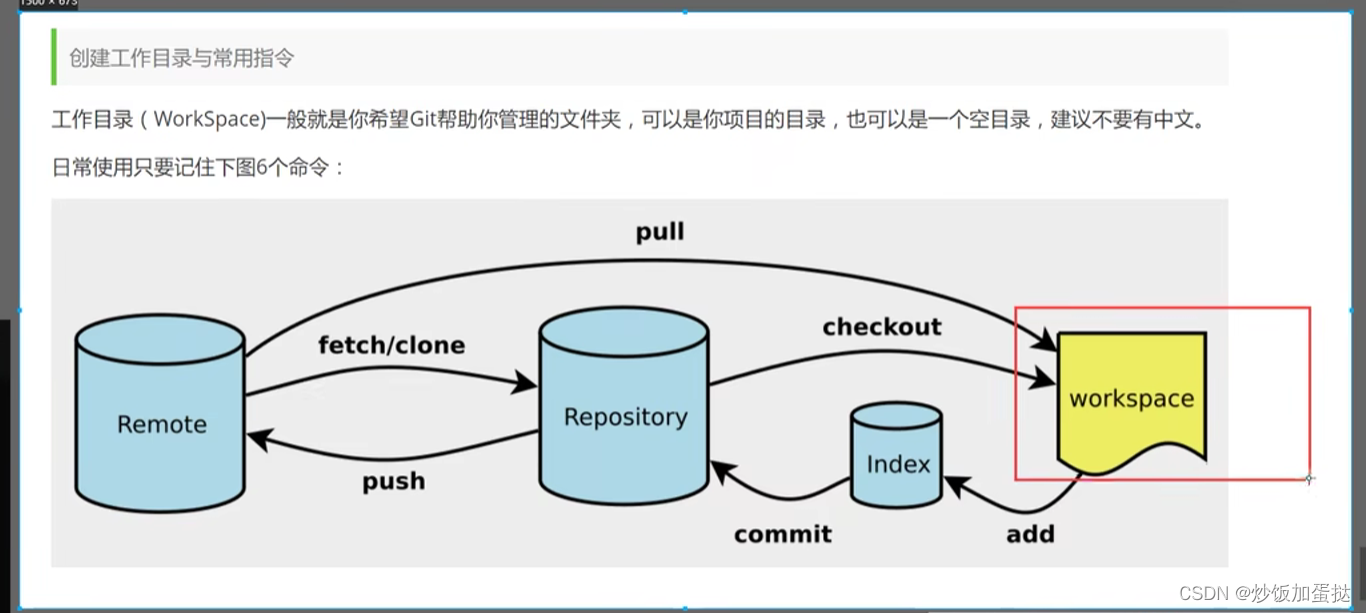
创建本地仓库(初始化)
git init 创建全新的仓库
git clone 克隆全新的仓库
git的文件操作
文件的4种状态 Untracked ,Unmodify ,Modified ,staged
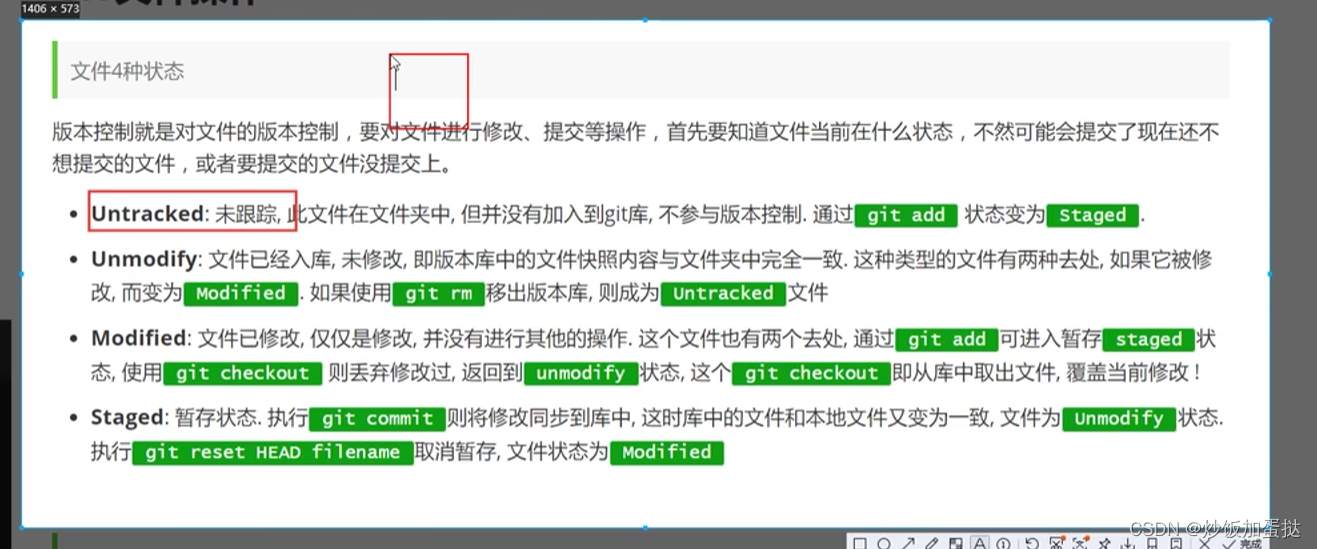
git add . 添加所有文件到暂存区
git commit -m”消息内容“ 提交暂存区的东西到本地仓库 -m为提交信息
忽略文件
8.使用码云
登陆注册
设置本机绑定SSH公匙,实现免密登陆
ssh-keygen -t rsa
生成公匙 在C:\Users\abcd\.ssh\id_rsa.pub复制粘贴即可
使用码云建立自己的仓库
9.IDEA中集成Git操作
新建项目,绑定git:将远程的git文件目录拷贝到项目中即可
注:红色为选中状态,绿色为提交
修改文件,使用idea操作git
git add .和git commit -m”消息内容“ 和git push即可
提交测试
10.git的分支

多个分支并行执行,导致代码不冲突,同时存在多个版本
master主分支应非常稳定,一般不允许在上面工作,工作一般在新建的dev分支工作,工作完要发布或dev非常稳定可以合并在主分支
MySQL与JDBC的使用(上)
前端(页面;展示,)
后台(连接点,连接数据库JDBC,连接前端(控制,控制视图跳转,和给前端传递数据))
数据库(存数据,txt,Excel,word)
一.
1.数据库的分类
关系型数据库(SQL):MySQL,Oracle 表与表之间,行与列之间的关系数据存储
非关系型数据库(NOSQL): Redis,MongDB 对象存储,通过对象属性决定
DBMS(数据库管理系统)
2.SQLyog的下载
3.操作
每一个sqlyog的执行操作,本质上对应了一个sql,
创建数据库
新建一张表
查看表:尝试添加多条记录
4.基本的命令行操作
http://t.csdn.cn/TM7Op
DDL 定义
DML 操作
DQL 查询
DCL 控制
二.操作数据库
http://t.csdn.cn/H8OHA(了解即可)
创建数据库,删除数据库,使用数据库,查询数据库
注:将用可视化操作名创建的使用show后复制粘贴即可变成sql语句
例子:show create database 名 查看创建数据库的语句
show create 名 查看数据表的定义语句
desc 名 显示表的结构
1.数据库的列类型
https://learn.microsoft.com/zh-cn/sql/t-sql/data-types/data-types-transact-sql?view=sql-server-ver16
重要 int varchar text datatime timestamp
注意:不要使用NULL进行运算,结果为NULL
2.数据库的字段属性(重点)
https://zhuanlan.zhihu.com/p/136958310
unsigned 无符号
zerofill 0填充
自增 自动在上一条语句+1(默认)设置唯一主键index,必须为整数类型,可以自定义起始值与步长
非空
默认
3.MYISAM与InnoDB的区别
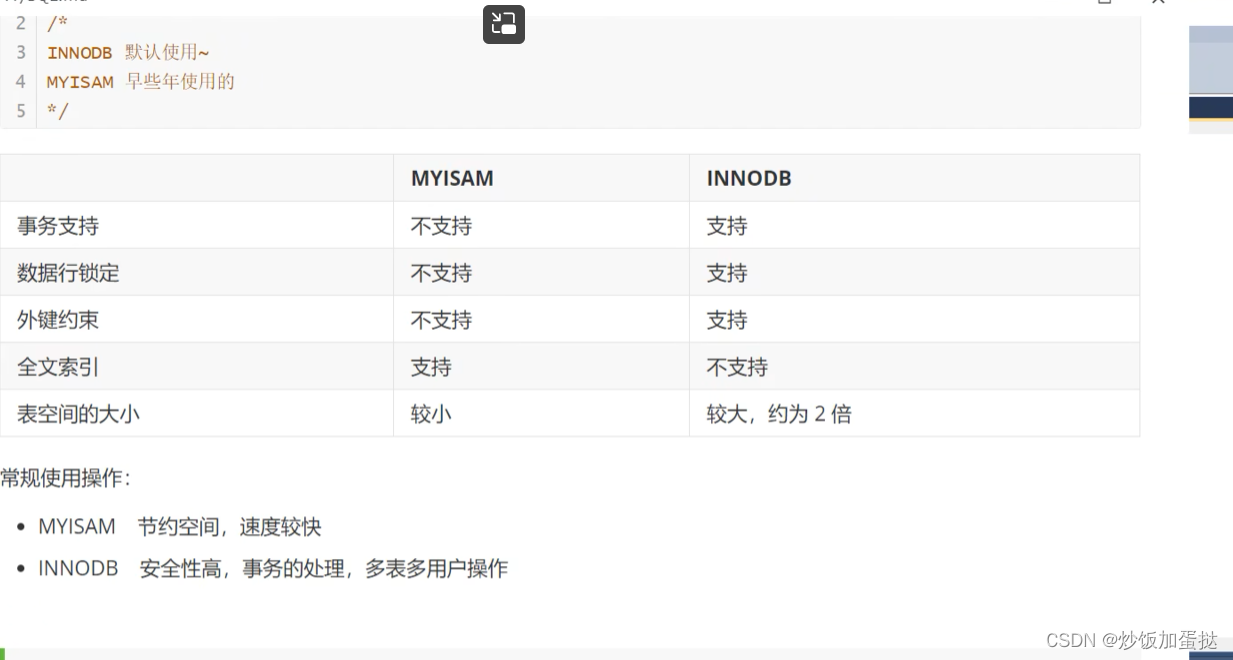

设置数据库表的字符集编码,不设置为mysql默认字符集编码,不支持中文
4.修改和删除数据表字段