文章目录
- 一、模型简介
- 1.1 加法分解模型
- 1.2 乘法分解模型
- 1.3 分析步骤
- 二、案例
- 2.1 背景 & 数据 & python包
- 2.2 分析过程
一、模型简介
1.1 加法分解模型
加法分解模型适用于随着时间推移趋势和季节性变化不断累加,并且随机波动比较稳定的时间序列数据。该模型假设原始时间序列由三个组成部分相加而成:
Y
t
+
S
t
+
R
t
Y_{t}+S_{t}+R_{t}
Yt+St+Rt
其中,
- Y t Y_{t} Yt:实际观测值
- T t T_{t} Tt:趋势(通常用指数函数来表示)
- S t S_{t} St:季节指数(一般通过计算每个季节的平均值得到)
- R t R_{t} Rt:残差(无法被趋势和季节性解释的部分)
1.2 乘法分解模型
乘法分解模型适用于随着时间推移趋势和季节性变化呈现出指数增长或衰减的时间序列数据。该模型假设原始时间序列由三个组成部分相乘而成:
Y
t
∗
S
t
∗
R
t
Y_{t}*S_{t}*R_{t}
Yt∗St∗Rt
注: 在实际应用中,加法分解模型是比较常见的模型,可以使用线性回归、多项式回归等方法拟合趋势和季节性部分,而乘法分解模型则更适用于呈现出指数增长或衰减趋势的时间序列数据。
1.3 分析步骤
- 1、观察原始数据趋势;
- 2、确定周期;
- 3、数据分解(趋势、季节指数、残差);
- 4、结果解读
二、案例
2.1 背景 & 数据 & python包
- 背景:分析某饮料产品2022.1-2023.3期间在上海的销售趋势,采用加法分解模型。
- 数据:
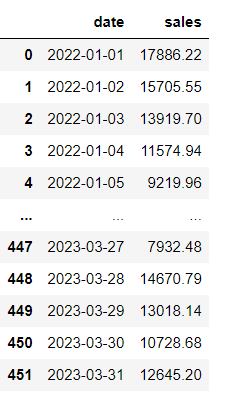
- statsmodels.tsa.seasonal_decompose 介绍:
from statsmodels.tsa.seasonal import seasonal_decompose
result = seasonal_decompose(
x, # 要分解的时间序列数据
model='additive', # 分解模型,可以是 'additive' (加法)或 'multiplicative'(乘法)
filt=None, # 最小二乘滤波器系数
period=None, # 时间序列的季节周期,如果未指定,则自动检测
two_sided=True, # 是否使用双侧滤波器
extrapolate_trend=0 # 在不充分观察到较长时间趋势的情况下,是否应该扩展趋势组件
)
该函数返回一个 DecomposeResult 对象,其中包含分解出的趋势、季节性和残差成分等信息,可以通过下方代码来实现获取:
decomposition = seasonal_decompose(df['col_name'],freq=7)
trend = decomposition.trend
seasonality = decomposition.seasonal
residual = decomposition.resid
# 创建一个新的DataFrame来存储趋势、季节性和残差
decomposed_df = pd.DataFrame({'Trend': trend, 'Seasonality': seasonality, 'Residual': residual})
decomposed_df
2.2 分析过程
加载相关库
import pandas as pd
from statsmodels.tsa.seasonal import seasonal_decompose
import seaborn as sns
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
%matplotlib inline
读取数据
df = pd.read_csv('data.csv')
绘制销售曲线
# 设置绘图风格
sns.set_style("whitegrid")
# 设置画布大小、精度
plt.figure(figsize = (16,4), dpi = 200)
# 绘制曲线图
ax = sns.lineplot(x='date', y='sales', data=df, color='blue', linewidth=1)
# 解决X轴密集问题:https://blog.csdn.net/small__roc/article/details/126950537?spm=1001.2014.3001.5502
ax.xaxis.set_major_locator(ticker.MultipleLocator(base=40))
# 添加标题和轴标签
plt.title('Sales Curve')
plt.xlabel('Date')
plt.ylabel('Sales')
# 显示图形
plt.show()
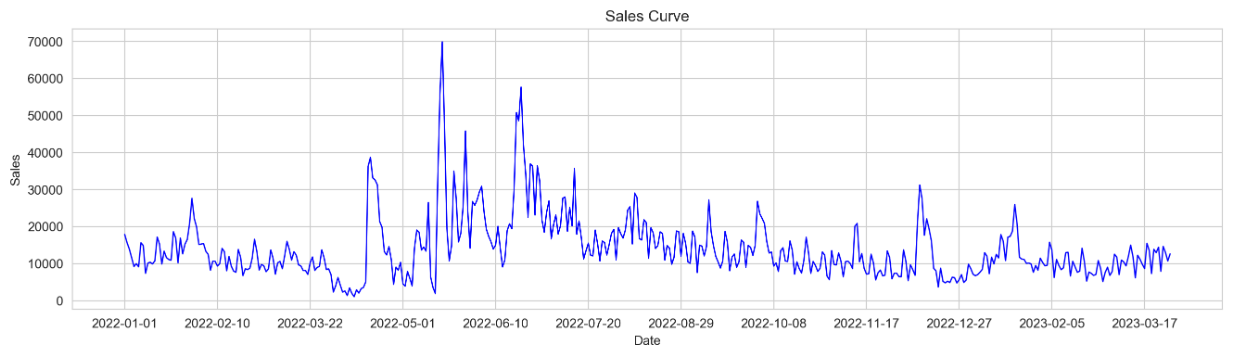
-
周期确定:饮料消费品线下销售一般会有:周末(或节假日)比工作日销量高、天气严热比冷寒销量高的特点,本文为了简化下模型,把周期设置为7天。 -
趋势分解
df.set_index("date",inplace=True)
decomposition = seasonal_decompose(df['sales'],period=7)
trend = decomposition.trend
seasonality = decomposition.seasonal
residual = decomposition.resid
# 创建一个新的DataFrame来存储趋势、季节性和残差
decomposed_df = pd.DataFrame({'Trend': trend, 'Seasonality': seasonality, 'Residual': residual})
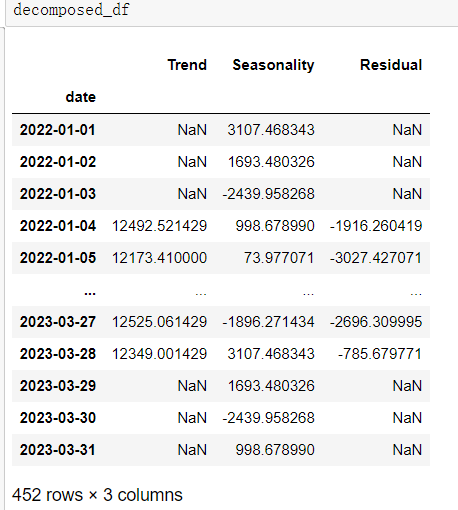
绘制分解后的数据曲线
colors = ['red', 'orange', 'green']
linestyles = ['-', '--', ':']
linewidths = [1.5, 1.5, 1.5]
markers = [None, 's', 'o']
markersizes = [1, 1, 1]
for i, col in enumerate(decomposed_df.columns):
decomposed_df[col].plot(
kind='line',
color=colors[i],
linestyle=linestyles[i],
linewidth=linewidths[i],
marker=markers[i],
markersize = markersizes[i],
figsize=(16, 4)
)
# 添加标题和轴标签
plt.title('Decomposed Sales Curve')
plt.xlabel('Date')
plt.ylabel('Value')
# 添加图例
plt.legend(decomposed_df.columns)
plt.show()
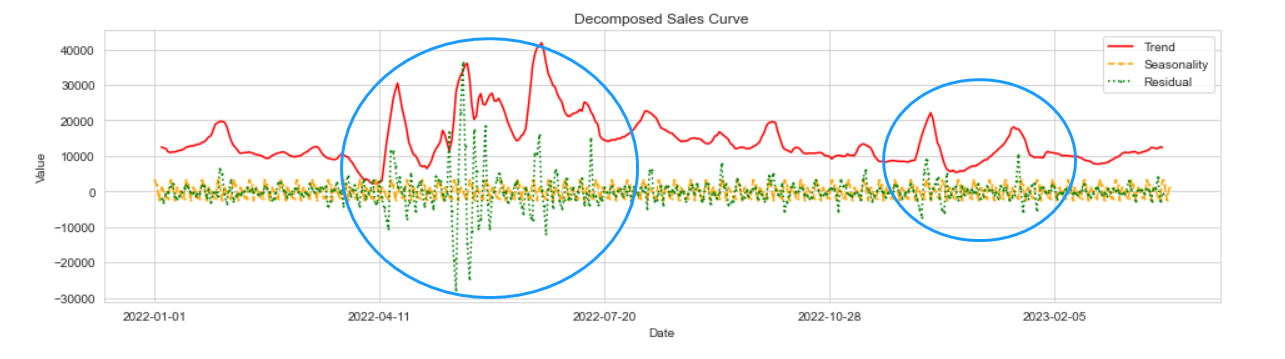
结果分析:
1、销量趋势的高点在4-7月份,但很明显去年这段时间残差波动非常大,说明存在异常情况(22年上海3-5月份口罩事件);
2、另一处销量趋势的高点在23年1-2月份,期间残差波动也存在异常,可能的原因是春节或某产品销量猛增,具体还需进一步分析。