📝个人主页：爱吃炫迈
💌系列专栏：数据结构与算法
🧑‍💻座右铭：道阻且长，行则将至💗

---

二分查找

---

二分查找也称折半查找（Binary Search），它是一种效率较高的查找方法。

• 但是，二分查找要求线性表必须采用顺序存储结构，而且表中元素按关键字有序排列。
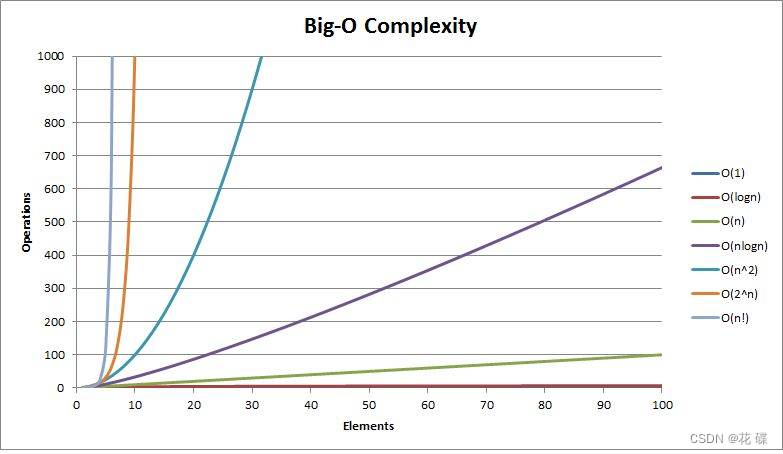
• 相比把整个数组遍历一次的O（n)复杂度，二分查找可以把复杂度降低到O（logn);

算法要求

---

1. 必须采用顺序存储结构
2. 必须按关键字大小有序排列

查找过程

---

1. 首先，假设表中元素是按升序排列，将表中间位置记录的关键字与查找关键字比较，如果两者相等，则查找成功；
2. 否则利用中间位置记录将表分成前、后两个子表；
3. 如果中间位置记录的关键字大于查找关键字，则进一步查找前一子表，否则进一步查找后一子表；
4. 重复以上过程，直到找到满足条件的记录，使查找成功；或直到子表不存在为止，此时查找不成功。

静图演示：

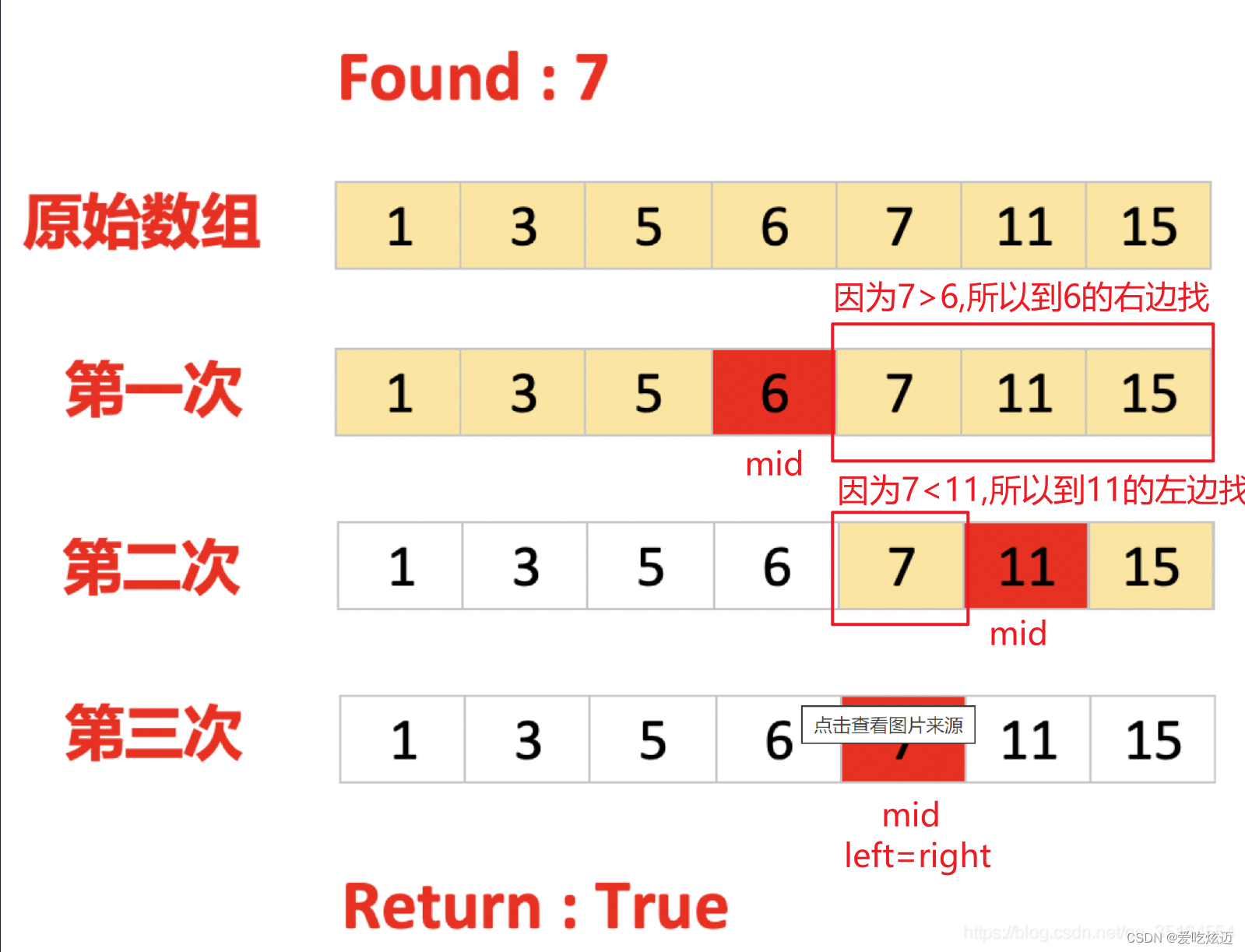
看到这里是不是想说一句二分查找就这？so easy~🤓
确实，二分查找的逻辑很简单，但是！二分查找涉及很多边界条件，特容易写不好。😭
例如到底是 while(left < right) 还是 while(left <= right)，
到底是right = middle呢，还是要right = middle - 1呢？

二分法的两种写法

---

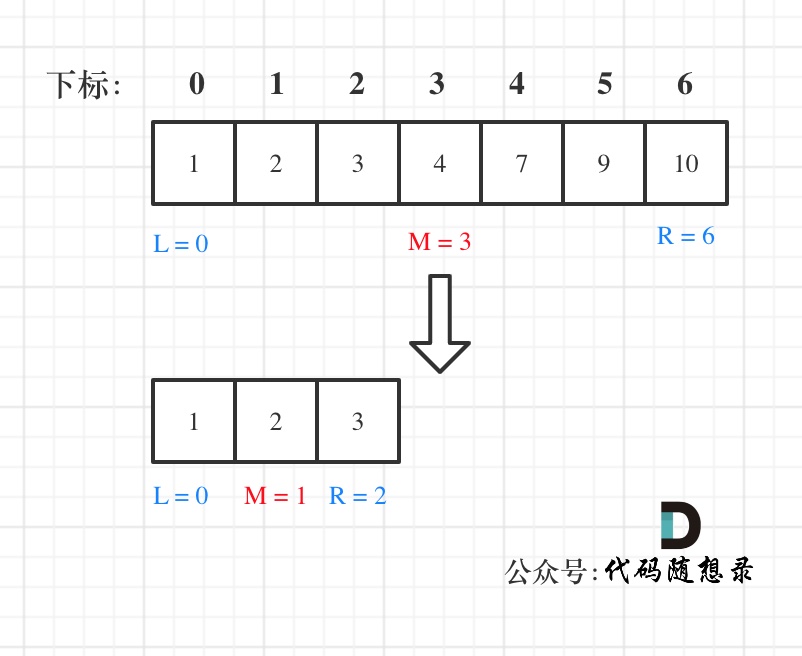
1. 左闭右闭 [left,right]

我们定义 target 是在一个在左闭右闭的区间里，也就是[left, right] （这个很重要非常重要）。

区间的定义这就决定了二分法的代码应该如何写，因为定义target在[left, right]区间，所以有如下两点：

• while (left <= right) 要使用 <= ，因为left == right是有意义的，所以使用 <=
• if (nums[middle] > target) 因为当前nums[middle]不等于target，去左区间继续寻找，right 要赋值为 middle - 1，因为当前这个nums[middle]一定不是target，那么接下来要查找的左区间结束下标位置就是 middle - 1

例如在数组：1,2,3,4,7,9,10中查找元素2，如图所示：

代码演示：

var search = function(nums, target) {
    // right是数组最后一个数的下标，num[right]在查找范围内，是左闭右闭区间
    let mid, left = 0, right = nums.length - 1;
    // 当left=right时，由于nums[right]在查找范围内，所以要包括此情况
    while (left <= right) {
        // 位运算 + 防止大数溢出
        mid = left + ((right - left) >> 1);
        // 如果中间数大于目标值，要把中间数排除查找范围，所以右边界更新为mid-1；如果右边界更新为mid，那中间数还在下次查找范围内
        if (nums[mid] > target) {
            right = mid - 1;  // 去左面闭区间寻找
        } else if (nums[mid] < target) {
            left = mid + 1;   // 去右面闭区间寻找
        } else {
            return mid;
        }
    }
    return -1;
};

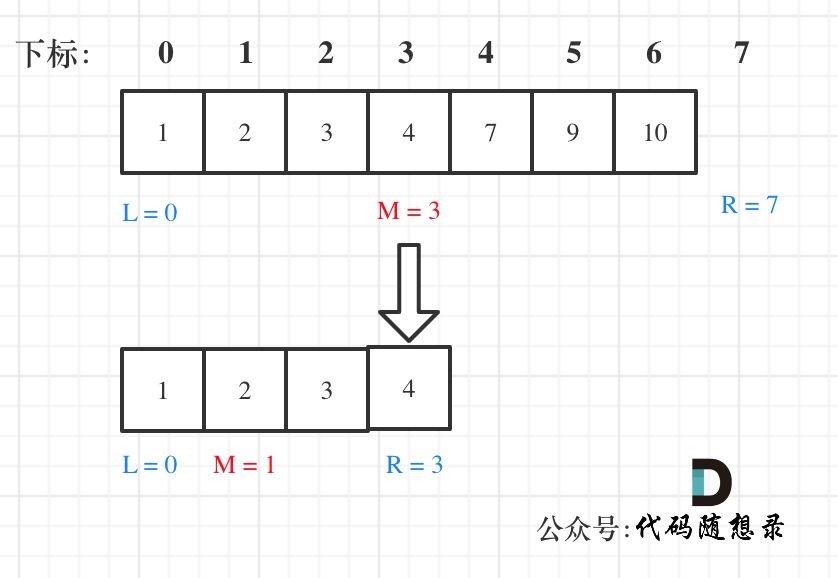
2. 左闭右开 [left,right)

如果说定义 target 是在一个在左闭右开的区间里，也就是[left, right) ，那么二分法的边界处理方式则截然不同。

有如下两点：

• while (left < right)，这里使用 < ,因为left == right在区间[left, right)是没有意义的
• if (nums[middle] > target) right 更新为 middle，因为当前nums[middle]不等于target，去左区间继续寻找，而寻找区间是左闭右开区间，所以right更新为middle，那么接下来要查找的左区间结束下标位置就是 middle ，但！下一个查询区间不会去比较nums[middle]

例如在数组：1,2,3,4,7,9,10中查找元素2，如图所示：（注意和方法一的区别）

代码演示

var search = function(nums, target) {
    // right是数组最后一个数的下标+1，nums[right]不在查找范围内，是左闭右开区间
    let mid, left = 0, right = nums.length;    
    // 当left=right时，由于nums[right]不在查找范围，所以不必包括此情况
    while (left < right) {
        // 位运算 + 防止大数溢出
        mid = left + ((right - left) >> 1);
        // 如果中间值大于目标值，中间值不应在下次查找的范围内，但中间值的前一个值应在；
        // 由于right本来就不在查找范围内，所以将右边界更新为中间值，如果更新右边界为mid-1则将中间值的前一个值也踢出了下次寻找范围
        if (nums[mid] > target) {
            right = mid;  // 去左区间寻找
        } else if (nums[mid] < target) {
            left = mid + 1;   // 去右区间寻找
        } else {
            return mid;
        }
    }
    return -1;
};

LeetCode（持续更新····）

---

1. 二分查找

/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number}
 */
var search = function (nums, target) {
  let left = 0;
  let right = nums.length - 1;
  while (left <= right) {
    const mid = Math.floor((right - left) / 2) + left;
    if (nums[mid] == target) {
      return mid;
    } else if (nums[mid] > target) {
      right = mid - 1;
    } else {
      left = mid + 1;
    }
  }
  return -1;
};

💞总结💞

希望我的文章能对你学习二分查找有所帮助！