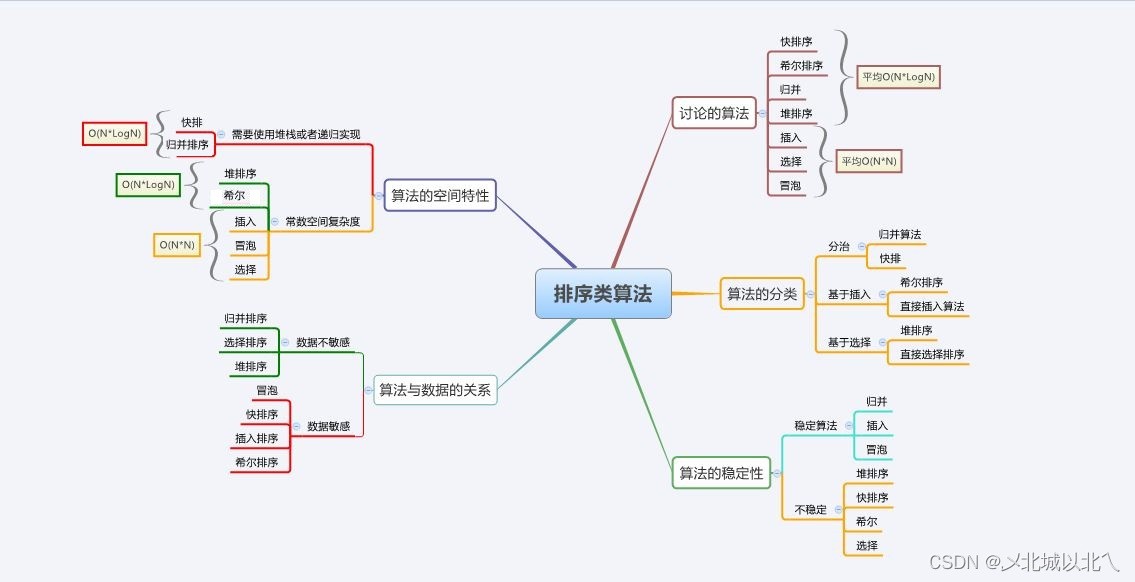
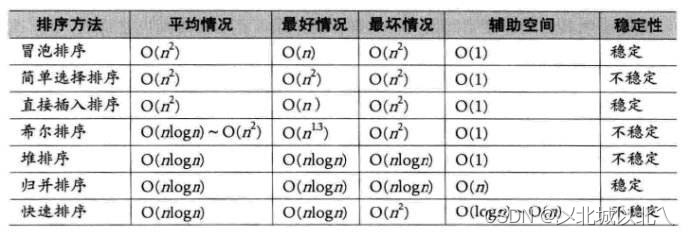
一、非递归实现快排

        在某些情景下，递归可以利用分治思想，将一个问题转化为多个子问题，再转化为更多个最小规模的子问题。从而帮助我们解决问题。

        但是，递归可能在效率和内存上产生问题。现如今，由于编译器的进一步优化，效率上的问题已经开始可以被接受，但内存上还会产生问题。

        这是因为递归的过程是在栈区上开辟和销毁函数栈帧，如果递归层数过深，（如快排退化为O(N^2)）时，就会导致栈溢出(StackOverFlow)，使程序崩溃，这就要求我们拥有将递归改成非递归的能力。

        1、按照递归逻辑，利用循环模拟递归的过程，是一种普遍的方法。

        2、利用合适的数据结构，例如栈(Stack)等。
        这是因为，函数递归的过程，变化的实际上是函数的参数，它们各自保存在各自的函数栈帧的相应区域，从而完成相似的工作。当我们使用数据结构时，就要通过合适的数据结构，将这些参数保存下来，并在合适的位置取出，从而模拟出递归的过程。

//  利用栈非递归实现快排，类似于前序遍历
//  栈里保存的是  原来递归中改变的参数
void QuickSortNonR(int* arr, int left, int right)
{
	ST s;
	STInit(&s);

	STPush(&s, right);
	STPush(&s, left);

	while (!STEmpty(&s))
	{
		// 取两次栈顶元素，作为接下来排序的区间
		int begin = STTop(&s);
		STPop(&s);
		int end = STTop(&s);
		STPop(&s);

		//排序的过程
		int keyi = QSortByPtrs(arr, begin, end);

		// 排序完后，将后续要排序的子区间入栈
		// [begin,keyi-1] [keyi+1,end]
		//  入栈的区间信息要保证是有效的
		//(为了先进行左区间排序，所以让右区间先入栈)
		if (keyi + 1 < end)
		{
			STPush(&s, end);
			STPush(&s, keyi+1);
		}
		if (begin < keyi-1)
		{
			STPush(&s, keyi-1);
			STPush(&s, begin);
		}

	}
	STDestroy(&s);
}

快速排序的非递归过程类似于前序遍历的过程。先对现在的位置进行排序，然后对左子区间和右子区间分别递归。

具体过程为：root0->rootL1->rootL2……->rootLN，先把左子树的根全部遍历完，然后再对rootLN的左右叶子排序，但由于左右叶子没有数据，直接返回。

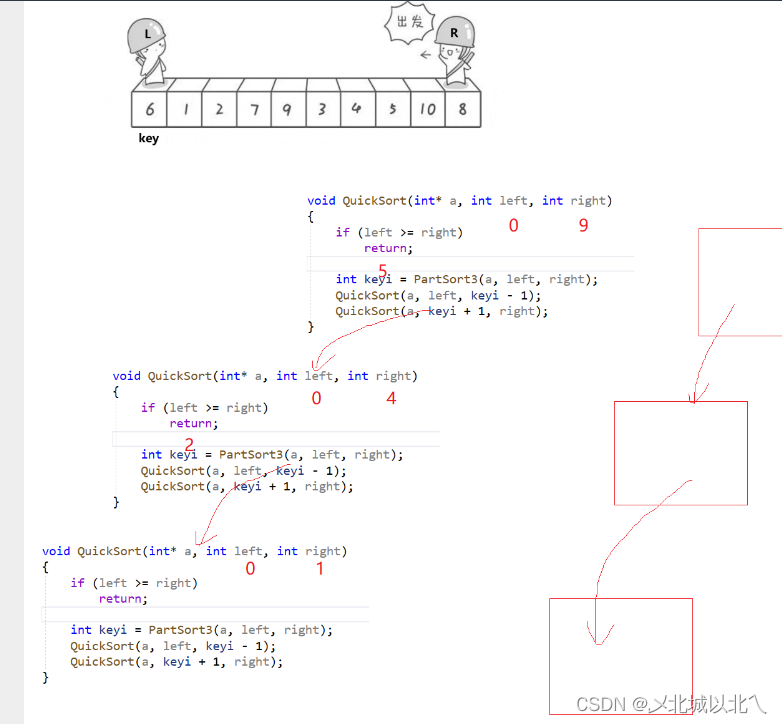
通过递归展开图，我们可以清楚的知道需要保存的参数是left和right。

由于我们习惯上的前序遍历是  root->left->right，而我们使用的数据结构是栈，因此对于先排序的left，就要后入栈，后取出的right就要先入栈。

先创建一个栈s，并初始化，由于一开始为空栈，先将初始的right和left入栈。

 

 只要栈不为空，就可以进行非递归排序。

分别用begin和end取出之前入栈的left和right(left在right上面，因此先取出)。取出后不要忘了Pop掉，以便取出下一个数据。

取出后，调用之前快排的部分函数，完成对[left,right]区间的排序，并且返回排好位置的下标keyi。

此时相当于完成了root位置的访问，即排序。

然后为了模拟后续左右子树的递归过程，又需要将新的参数入栈。

此时keyi将整个数组分为2个区间。[begin,keyi-1]  [keyi+1,end]。根据先进后出和后进先出原则，仍然是右边先进，即按照 end  keyi+1  keyi-1  begin的顺序入栈。

注意：入栈的时候最好判断一下区间是否存在(相当于递归时判断返回值)，如果区间不存在还入栈，下一轮又取出，影响效率，直接不让它入栈即可。

总结：快排的非递归类似于前序遍历，通过对目前根位置排序，得到keyi，然后可以得到两个区间[begin,keyi-1]  [keyi+1,end]，再利用栈将区间的参数保存，然后按照入栈出栈的顺序约束，一步一步访问到叶子，利用分治思想，完成整体的排序。

二、归并排序介绍

首先，先了解一下归并的过程。即将两组数据arr1和arr2，它们各自均为升序（假设目标为升序）

然后开辟一个临时数组tmp，从它们各自的第一个元素开始比较，较小的那个就往tmp数组里放，直到其中一个数组全部被拷贝完。然后再将另一个数组中的后续升序部分拷贝的tmp中，则此时tmp就是arr1和arr2归并后的结果。

 

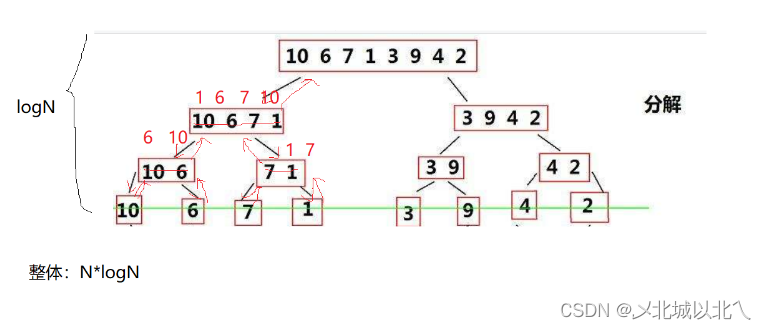
上图为一次归并排序的内部过程。利用 i  begin1  begin2  三个指针/下标  标记在3个数组中的位置，然后进行比较+拷贝的过程。

 

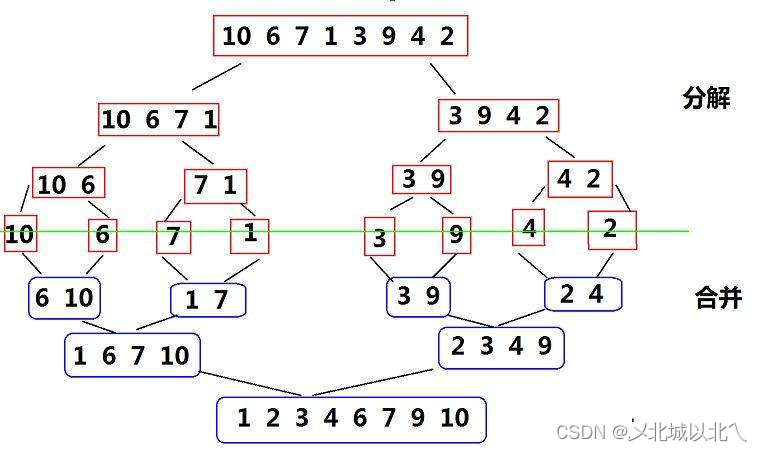
         与快排的前序遍历不同，归并排序需要先保证左右区间均为有序，因此需要先对其左右子区间进行归并排序，最后再对根位置排序，类似于后续遍历的过程。

一直分解区间，直到剩下1个数据(类比堆排序，无数据时可认为是大堆/小堆)，此时1个数据可认为是升序/降序。然后进行 1-1归并，归并完变成有2个数据的有序区间。然后再2-2归并，4-4归并，直到整个数组完全归并。

        下面为动图：

归并的过程为标准的二分，共有logN层，每层N个，时间复杂度为O(NlogN) 

 三、递归实现归并排序

//递归实现归并排序的 子函数
void _MergeSort(int* arr, int* tmp, int begin, int end)
{
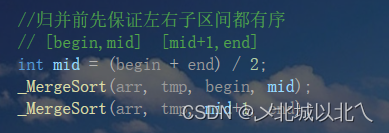
	if (begin >= end)
		return;

	//归并前先保证左右子区间都有序
	// [begin,mid]  [mid+1,end]
	int mid = (begin + end) / 2;
	_MergeSort(arr, tmp, begin, mid);
	_MergeSort(arr, tmp, mid+1, end);

	//  归并排序的过程
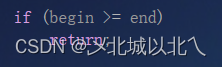
	int i = begin;// 不能给0，要从起始位置开始
	int begin1 = begin;
	int begin2 = mid + 1;
	int end1 = mid;
	int end2 = end;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (arr[begin1] < arr[begin2])
		{
			tmp[i++] = arr[begin1++];
		}
		else
		{
			tmp[i++] = arr[begin2++];
		}
	}
	// 其中一个数组已经完全归并完了，再把另一个给归并
	while (begin1 <= end1)
	{
		tmp[i++] = arr[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[i++] = arr[begin2++];
	}
	//  最后再将tmp数组中的数据拷贝回要排序的arr数组
	//memmove(arr, tmp, sizeof(int) * (end - begin + 1));
	memcpy(arr + begin, tmp+begin, sizeof(int) * (end - begin + 1));


}
//递归实现归并排序
void MergeSort(int* arr, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (NULL == tmp)
	{
		perror("malloc fail");
		return;
	}
	// 为了避免多次malloc，在此函数中不递归
	// 创建一个子函数，递归子函数，使用的是此函数中malloc的数组
	_MergeSort(arr, tmp, 0, n-1);

	free(tmp);
}

实际上，我们的归并排序，是将一个数组分为两个区间，再看作是2个数组。

对于每个1-1归并的最小规模子问题，我们应该开辟一个大小为2的数组来保存它们排序后的结果，但这样一来，我们就需要开辟N^2级别个数组，由于malloc开辟过程中的损耗，我们选择直接开一个有n个数据的数组tmp，后续的递归拷贝过程用下标来控制。

找到中间位置mid，然后二分为左右区间，（二分是为了保证递归深度最小，防止栈溢出），对左右区间分别调用归并排序。

 

直到递归区间只有1个数据（默认为有序），或区间不存在时返回。

 

然后对该区间进行归并排序。

用begin1、end1、begin2、end2代表 [begin,mid] [mid+1,end]这两个区间。

 

 之前归并时拷贝到了tmp临时数组，最后一步再拷贝回原arr数组。

注意：拷贝的起始位置是由区间下标标记的，要拷贝到正确的位置上。

        下面给出一张参照图。

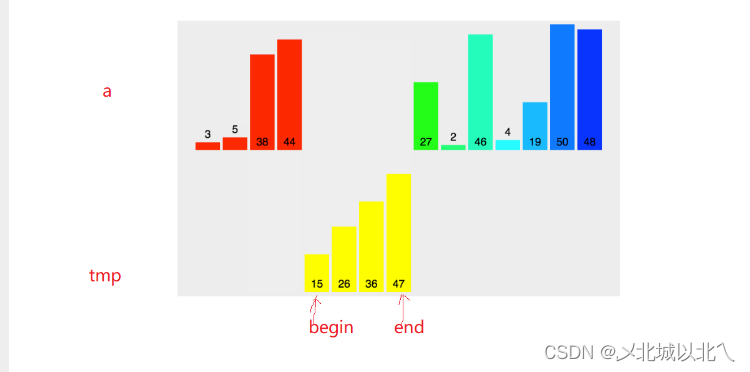
 归并到tmp数组的范围是[begin,end],因此拷贝回arr数组的范围也应该是[begin,end]。

四、非递归实现归并排序

由于归并排序的递归逻辑为后序遍历，因此无法像快排那样利用栈来模拟实现。因为在归并排序前，要先保证其左右子区间均有序。

因此，前n-1层都不能直接排序，只能先排最后一层，然后从下到上，依次排序。

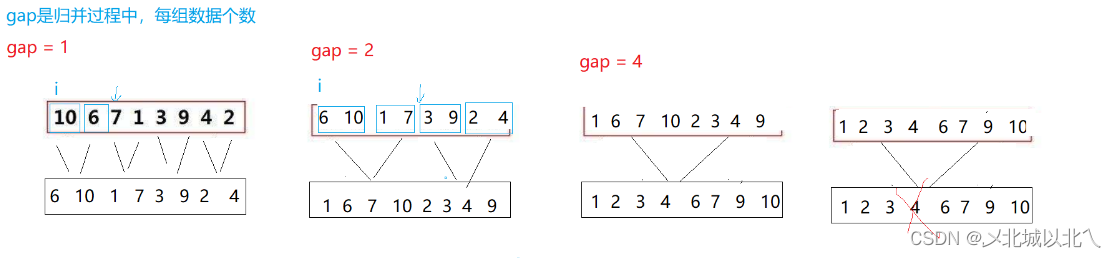
先将数据分解为单个有序，然后对所有数据进行1-1排序，然后2-2排序，直到排序完。（这个过程可以通过循环控制，其中gap为要排序的单组数据的个数）。

//非递归实现归并排序
void MergeSortNonR(int* arr, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (NULL == tmp)
	{
		perror("malloc fail");
		return;
	}
	int gap = 1;

	while (gap<n)
	{
		for (int i = 0; i < n; i += 2 * gap)
		{
			//int j = i;//保存一下循环变量初始值，或者用另一个变量遍历tmp
			int j = i;
			int begin1 = i, end1 = begin1 + gap - 1;
			int begin2 = begin1 + gap, end2 = end1 + gap;
			//归并排序的过程 [begin1,end1] [begin2,end2]
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (arr[begin1] <= arr[begin2])
				{
					tmp[j++] = arr[begin1++];
				}
				else
				{
					tmp[j++] = arr[begin2++];
				}
			}
			while (begin1 <= end1)
			{
				tmp[j++] = arr[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[j++] = arr[begin2++];
			}
			memmove(arr + i, tmp + i, sizeof(int) * (end2 - i + 1));
			//  end2-i+1为归并的区间范围
			//归并一部分拷贝一部分
		}
		gap *= 2;
	}
	free(tmp);
}

 i从0，即第一个位置开始，每次begin1=i,由于一组有gap个数据，所以end1=begin1+gap-1，然后begin2=begin1+gap，end2=end1+gap。

每次循环后，i+=2*gap,再进行后面2组的归并排序，直到将整个数组都排完，此时1-1排序以及全部完成。

gap*=2，进行下一轮的2-2排序，只要gap<n就可以进行2组之间的归并。

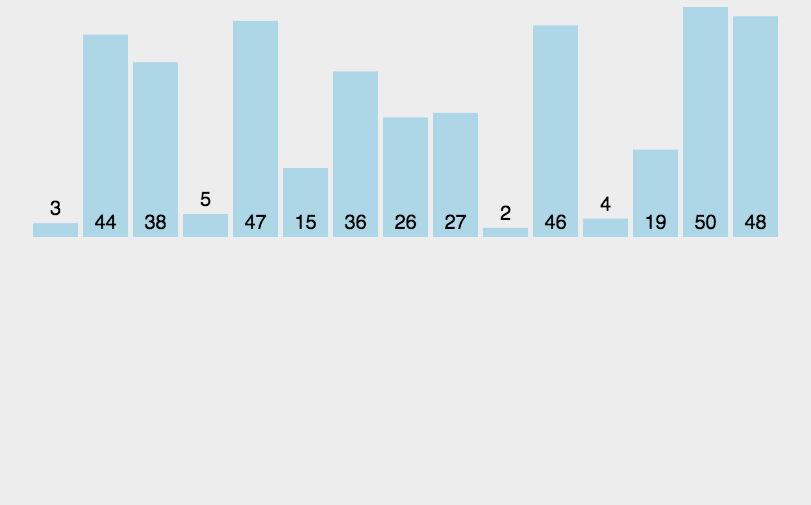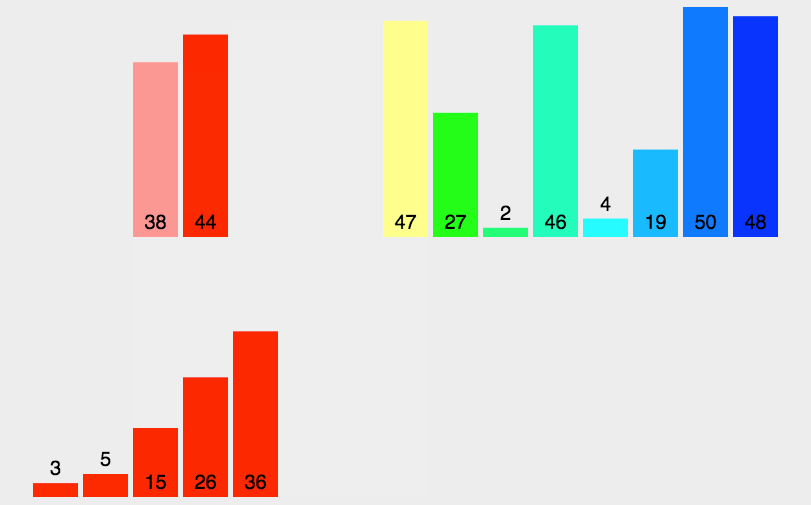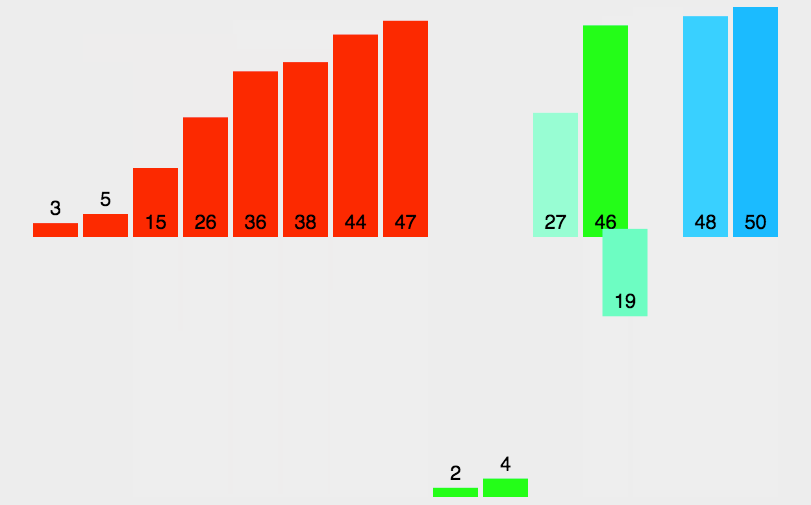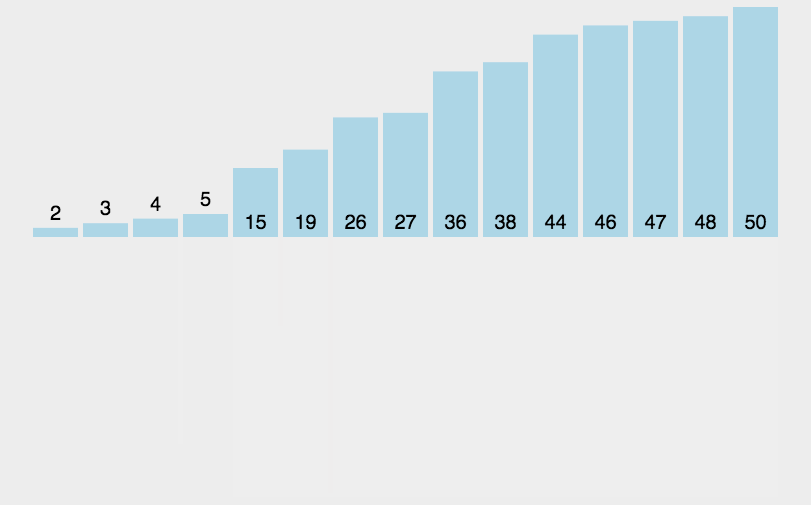
 在每次归并前，我们先将归并区间打印一下。

对于 10  6  7  1  3  9  4  2  5这样的9个数据，下标的范围应该是[0,8] 

但在打印的过程中，我们可以看到9  10  11  12  15等下标，这些下标是越界的。

这是因为，在完成一轮排序后，我们总是默认将gap变为2倍，然后对begin1、begin2、end1、end2进行gap关系上的赋值，因此，在数据总数N不为2,4,8,16……的2的倍数时，必然会发生越界，越界包括后面的访问和拷贝过程。

为了，防止越界，我们需要在排序前，对下标进行修正。

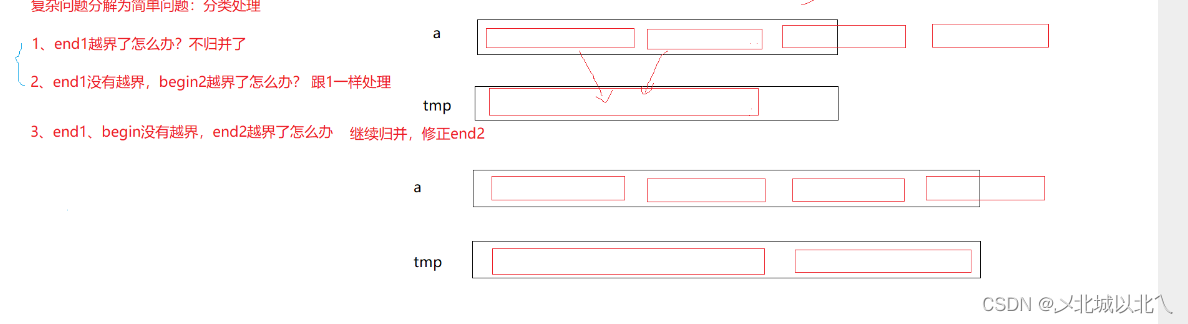
 由于begin1的值就是i，而i始终<n因此它不会越界。此时分3种情况讨论。

1、end1越界：此时arr1数组部分在界内，且有序，arr2数组[begin2,end2]完全在界外，因此可以不进行归并排序，直接保留界内的arr1数组。

2、begin2越界：此时arr1数组都在界内，且有序，arr2数组完全在界外，与1相同，不进行归并排序，直接保留所有的arr1数组。

3、end2越界：此时arr数组都在界内，且有序；arr2数组部分在界内，内部有序，还有部分在界外，有序arr1和arr2的部分  只是内部有序，因此需要对arr1和arr2的界内部分进行归并排序，需要对end2进行修正，改为n-1。 

修正后arr1范围仍为[begin1,end1],而arr2的范围变为[begin2,n-1]。

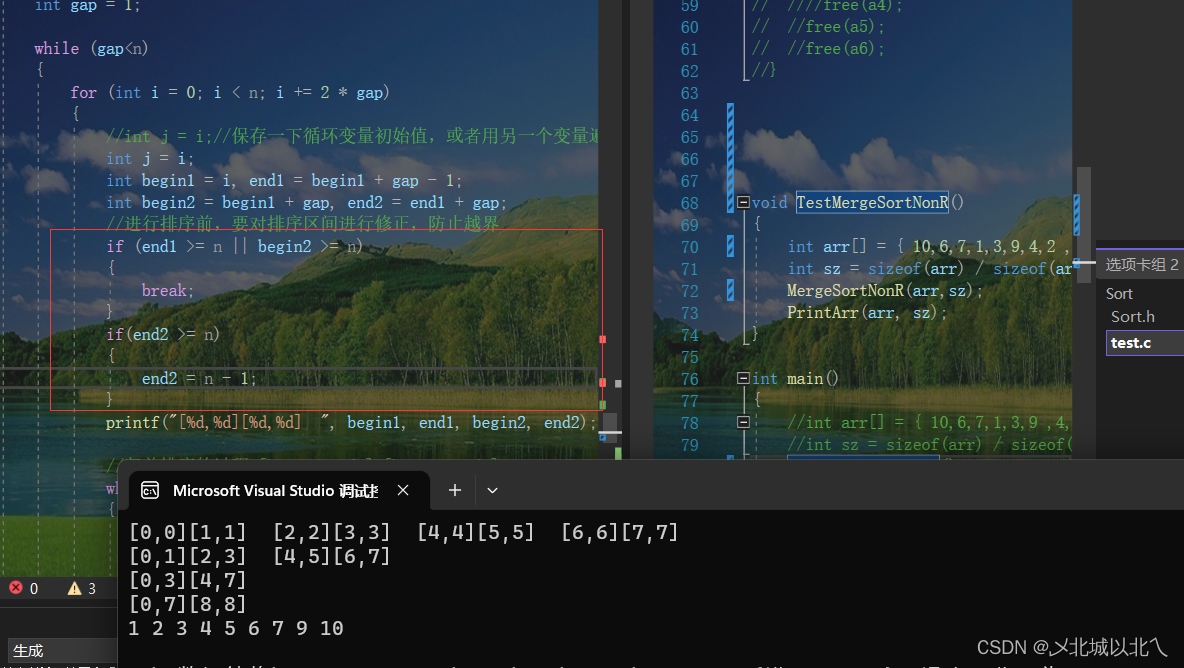
 添加了修正部分。前2种情况，直接不进行这2组归并，跳出到下一轮gap更大的归并过程中。

end2大于n时，将其修正为n-1，然后进行归并排序。

拷贝过程是任何一次归并排序后直接拷贝，无论是1-1归并还是2-2归并，都要拷贝先拷贝回arr数组，这是为了便于前面的break，可以直接跳出，不用再重复先拷贝到tmp， 又拷贝回arr的过程。

由于在任何一次归并排序中，i的位置不变，而begin1和begin2都会改变，要拷贝回arr+i，即这段区间的初始位置，拷贝总数为end2-i+1.

五、非比较排序--计数排序

对于我们之前讲的快排，归并排序，希尔排序等，都是通过比较2个数据的大小，来确定它们的相对位置的。

而计数排序通过以下规则实现：

1. 统计相同元素出现次数
2. 根据统计的结果将序列回收到原来的序列中

通过个数的统计，进行拷贝，不需要比较。

//计数排序
void CountSort(int* arr, int n)
{
	int min = arr[0];
	int max = arr[0];

	for (int i = 1; i < n; ++i)
	{
		if (arr[i] < min)
		{
			min = arr[i];
		}
		if (arr[i] > max)
		{
			max = arr[i];
		}
	}
	// 先找出来最大值和最小值，确定数据范围
	int range = max - min + 1;
	//计数数组 countA，记录每个数据出现的次数
	int* countA = (int*)calloc(range, sizeof(int));//前面的参数为个数，后面为每个的大小
	if (NULL == countA)
	{
		perror("calloc fail");
	}

	for (int i = 0; i < n; ++i)
	{
		countA[arr[i] - min]++;
	}
	//记录完每个数据出现的次数后，拷贝到原来的数组
	//  排序回原数组的过程
	int j = 0;

	for (int i = 0; i < range; ++i)
	{
		while ((countA[i])--)
		{
			arr[j++] = i + min;
		}
	}

	free(countA);
}

计数排序的特性总结：
1. 计数排序在数据范围集中时，效率很高，但是适用范围及场景有限。
2. 时间复杂度：O(N+range)
3. 空间复杂度：O(range)