本文已收录到 GitHub · AndroidFamily，有 Android 进阶知识体系，欢迎 Star。技术和职场问题，请关注公众号 [彭旭锐] 进 Android 面试交流群。

前言

大家好，我是小彭。

今天分享到一种非常有趣的数据结构 —— 前缀和数组。前缀和的思想本身很容易理解，同时也是理解更高难度的线段树、字典树等数据结构的基础。

那么，什么是前缀和，我们可以使用前缀和解决什么问题呢？今天我们就围绕这两个问题展开。

---

学习路线图：

---

1. 什么是前缀和

前缀和数组是一种用来高效地解决 “静态数据的频繁区间和查询” 问题的数据结构。

先举个例子，给定一个整数数组，要求输出数组在 $[i,j]$ 区间内元素的总和，这就是区间查询问题。这道题的暴力解法是很容易想到的，无非就是把 $[i,j]$ 区间中所有元素累计而已即可，时间复杂度是 $O(n)$，空间复杂度是 $O(1)$。

单次查询确实已经没有优化空间了，但如果进行频繁的区间和查询，很明显会有非常多重复的求和运算。例如，在查询 $[1,5]$ 区间和 $[1,10]$ 区间时，$[1,5]$ 这个子区间就被重复计算了。那么，有可能借助 “空间换时间”，在 $O(1)$ 时间复杂度内计算 $[5000,1000000]$ 上的区间和吗？

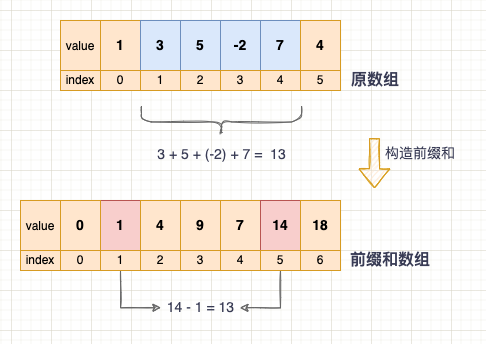
这就需要使用前缀和 + 差分技巧：

• 预处理阶段： 开辟一个前缀和数组，记录每个位置到所有前驱节点的累加和 $preSum$，总共需要 O(n) 时间；
• 查询阶段： 将区间左右端点的区间和相减，就可以在 $O(1)$ 时间得到这个区间中所有元素的累加和，避免了每次查询都需要 for 循环遍历整个区间求和。例如，要求 $[i,j]$ 区间的和，就是直接用 $preSum[j+1]-preSum[i]$ 获得。

前缀和示意图

---

2. 典型例题 · 区间和检索

理解以上概念后，就已经具备解决区间和问题的基本知识了。我们来看一道 LeetCode 上的前缀和典型例题：LeetCode 303. 区域和检索 - 数组不可变

LeetCode 例题

题解

class NumArray(nums: IntArray) {

    // 前缀和数组
    // 数组长度加一后不用考虑数组越界，代码更简洁
    private val preSum = IntArray(nums.size + 1) { 0 }

    init {
        for (index in nums.indices) {
            preSum[index + 1] = preSum[index] + nums[index]
        }
    }

    fun sumRange(i: Int, j: Int): Int {
        return preSum[j + 1] - preSum[i]
    }
}

代码很简单，其中前缀和数组 preSum 的长度要额外加 1 是为了简化数组越界判断。我们来分析它的复杂度：

• 时间复杂度： 构建前缀和数组的时间复杂度是 $O(n)$，查询的时间复杂度是 $O(m)$，$n$ 是数据量，$m$ 是区间和查询的次数；
• 空间复杂度： $O(n)$，使用了 长度为 $n+1$ 的前缀和数组。

另外，前缀和还适用于二维区间和检索，思路都是类似的，你可以试试看： LeetCode · 304. 二维区域和检索 - 矩阵不可变

---

3. 典型例题 · 前缀和 + 哈希表

继续看另一道前缀和与哈希表结合的例题：LeetCode 560. 和为 K 的子数组

LeetCode 例题

这道题就是在考前缀和思想，我们可以轻松地写出第一种解法：

题解

class Solution {
    fun subarraySum(nums: IntArray, k: Int): Int {
        // 1、预处理：构造前缀和数组
        var preSum = IntArray(nums.size + 1) { 0 }
        for (index in nums.indices) {
            preSum[index + 1] = preSum[index] + nums[index]
        }

        // 2、枚举所有子数组，使用「前缀和 + 差分」技巧计算区间和
        var result = 0
        for (i in nums.indices) {
            for (j in i until nums.size) {
                val sum_i_j = preSum[j + 1] - preSum[i]
                if (k == sum_i_j) {
                    result++
                }
            }
        }
        return result
    }
}

在这个题解中，我们枚举每个子数组，使用「前缀和 + 差分」技巧计算区间和为 K 的个数，我们来分析下它的复杂度：

• 时间复杂度： 一共存在 $n^2$ 个子数组，单次子数组的区间查询是 $O(1)$，所以整体的时间复杂度是 $O(n^2)$；
• 空间复杂度： $O(n)$。

时间复杂度有办法优化吗？我们发现，题目要求的是数组个数，而不关心具体的数组，所以我们不必枚举全部子数组（一共有 $n^2$ 个子数组）， 我们只需要在计算出当前位置的前缀和之后，观察之前的位置中是否存在前缀和正好等于 $preSum[j]-K$ 的位置，有的话，就说明它们之间的区间和就是 $K$。 把满足条件的个数累加起来，就是最终结果。

前缀和示意图

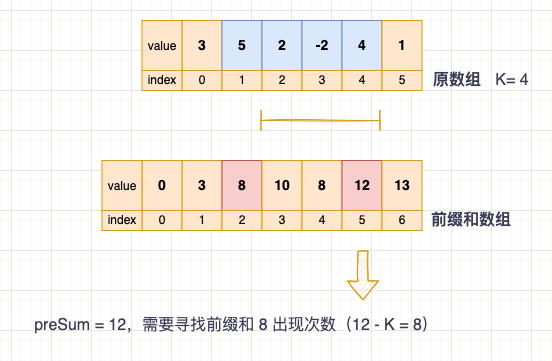
紧接着另一个问题是：怎么快速找到前缀和等于 $preSum[j]-K$ 的位置？聪明的你一定知道了—— 哈希表。 我们可以维护一个哈希表，记录前缀和出现的位置，就可以用 O(1) 找到它。 由于前缀和有可能会重复出现，而且我们只关心次数不关心位置，所以映射关系应该为 <前缀和 - 出现次数>。

题解

class Solution {
    fun subarraySum(nums: IntArray, k: Int): Int {
        var preSum = 0
        var result = 0

        // 维护哈希表<前缀和，出现次数>
        val map = HashMap<Int, Int>()
        map[0] = 1

        for (index in nums.indices) {
            preSum += nums[index]
            // 获得前缀和为 preSum - k 的出现次数
            val offset = preSum - k
            if (map.contains(offset)) {
                result += map[offset]!!
            }
            map[preSum] = map.getOrDefault(preSum, 0) + 1
        }
        return result
    }
}

我们来分析下它的复杂度：

• 时间复杂度： 每个元素只处理一次，整体时间复杂度是 $O(n)$；
• 空间复杂度： $O(n)$。

---

4. 典型例题 · 前缀和 + 单调队列

继续看一道前缀和与单调队列结合的例题，你可以先做一下第 53 题：

• LeetCode 53. 最大子数组和
• LeetCode 918. 环形子数组的最大和

LeetCode 例题

在第 53 题中，我们只需要维护一个当前观察到的最小前缀和变量，将其与当前的前缀和做差值，就可以得到以当前节点为右端点的最大的区间和。这一题就是考前缀和思想，相对简单。

第 53 题题解

class Solution {
    fun maxSubArray(nums: IntArray): Int {
        // 前缀和 + 单调：维护最小的前缀和
        var minPreSum = 0
        var result = Integer.MIN_VALUE
        var preSum = 0

        for (element in nums) {
            preSum += element
            result = Math.max(result, preSum - minPreSum)
            minPreSum = Math.min(minPreSum, preSum)
        }
        return result
    }
}

在第 918 题中，数组变为环形数组，环形数组的问题一般都会用 2 倍的 “假数据长度” 做模拟，求前缀和数组这一步大同小异。

关键在于： “子数组最多只能包含固定缓冲区 num 中的每个元素一次”，这意味随着观察的区间右节点逐渐向右移动，所允许的左区间会限制在一个滑动窗口范围内，以避免元素重复出现。因此，一个变量不再能够满足题目需求。

示意图

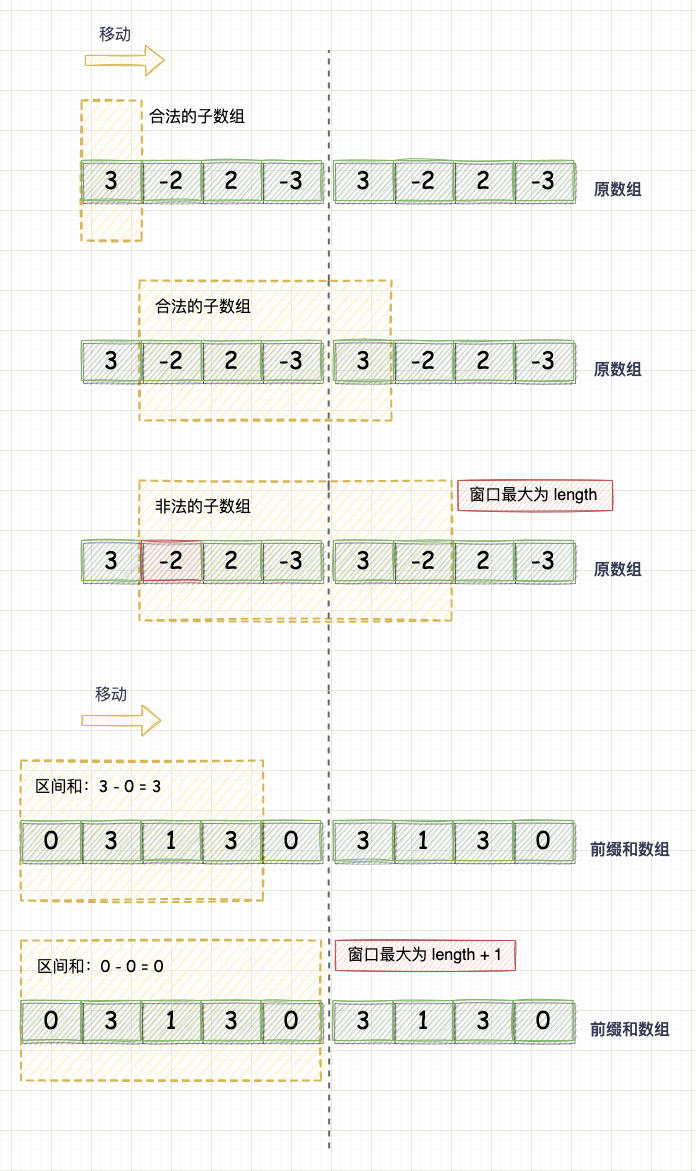
所以我们的问题就是要求这个 “滑动窗口中的最小前缀和”。Wait a minute! 滑动窗口的最小值？这不就是 使用单调队列解决 “滑动窗口最大值” 问题 这篇文章讲的内容吗，秒懂，单调队列安排一下。

第 918 题题解

class Solution {
    fun maxSubarraySumCircular(nums: IntArray): Int {
        val preSum = IntArray(nums.size * 2 + 1).apply {
            for (index in 0 until nums.size * 2) {
                this[index + 1] = this[index] + nums[index % nums.size]
            }
        }

        // 单调队列（从队头到队尾递增）
        val queue = LinkedList<Int>()
        var result = Integer.MIN_VALUE

        for (index in 1 until preSum.size) {
            // if：移除队头超出滑动窗口范围的元素
            // 前缀和窗口 k 为 length + 1，比原数组上的逻辑窗口大 1 位，因为区间的差值要找前一个节点的前缀和
            if (!queue.isEmpty() && queue.peekFirst() < index - nums.size /* index - k + 1 */) {
                queue.pollFirst()
            }

            // 从队头取目标元素
            result = Math.max(result, preSum[index] - (preSum[queue.peekFirst() ?: 0]))

            // while：队尾元素大于当前元素，说明队尾元素不再可能是最小值，后续不再考虑它
            while (!queue.isEmpty() && preSum[queue.peekLast()] >= preSum[index]) {
                // 抛弃队尾元素
                queue.pollLast()
            }
            queue.offerLast(index)
        }
        return result
    }
}

我们来分析它的时间复杂度：

• 时间复杂度： 构建前缀和数组 $O(n)$，前缀和数组中每个元素在单调队列中入队和出队 $1$ 次，因此整体时间复杂度是 $O(n)$;
• 空间复杂度： 构建前缀和数组 $O(n)$，最坏情况下（递减序列）所有元素都被添加到单调队列中，因此整体空间复杂度是 $O(n)$。

提示： 这道题还有使用 Kadane 算法 的 $O(1)$ 空间复杂度解法。

---

5. 总结

到这里，前缀和的内容就讲完了。文章开头也提到了， 前缀和数组是一种高效地解决静态数据的频繁区间和查询问题的数据结构，只需要构造一次前缀和数组，就能使用 O(1) 时间完成查询操作。

那么，在动态数据的场景中（即动态增加或删除元素），使用前缀和数组进行区间和查询是否还保持高效呢？如果不够高效，有其他的数据结构可以解决吗？你可以思考以下 2 道题：

• LeetCode · 307. 区域和检索 - 数组可修改
• LeetCode · 308. 二维区域和检索 - 矩阵不可变

更多同类型题目：

前缀和	难度	题解
303. 区间和检索 - 数组不可变	Easy	【题解】
724. 寻找数组的中心下标	Easy	【题解】
304. 二维区域和检索 - 矩阵不可变	Medium	【题解】
560. 和为 K 的子数组	Medium	【题解】
974. 和可被 K 整除的子数组	Medium	【题解】
1314. 矩阵区域和	Medium	【题解】
918. 环形子数组的最大和	Medium	【题解】
525. 连续数组	Medium	【题解】
1248. 统计「优美子数组」	Medium	【题解】

---

参考资料

• LeetCode 专题 · 前缀和 —— LeetCode 出品
• LeetCode 题解 · 560. 和为 K 的子数组 —— liweiwei1419 著
• 小而美的算法技巧：前缀和数组 —— labuladong 著
• 小而美的算法技巧：差分数组 —— labuladong 著