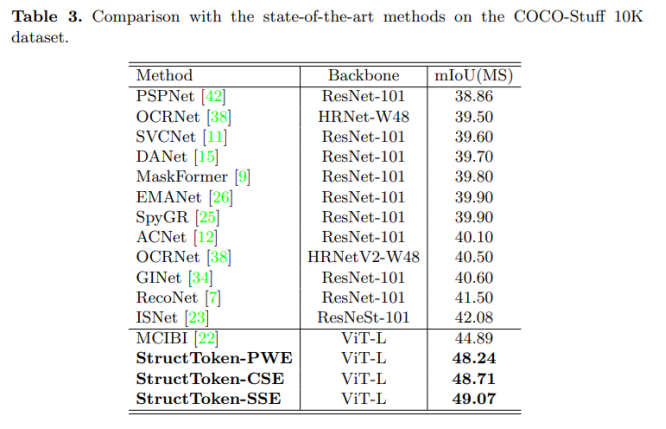
（一）椭圆锥面

（1）把z平方看成一个一直变大的常数，那么可以看出延z方向，是一个一直变大的椭圆。

（2）把一个x或y赋予0，显然是一个两条关于原点对称的直线。

由上即可判断出是一个关于x-y平面对称的椭圆锥面。

（二）椭球面

按x=0、y=0、z=0分别切开都是相同的椭圆，没什么好说的，椭球面。

（三）单叶双曲面

（1）按z=0切开是椭圆；

（2）按x=0或y=0切开都是双曲线。

所以单叶双曲面。

（四）双叶双曲面

（1）按y=0或z=0切开是双曲线；

（2）但按x=0切开是不存在的，说明没有点在y-z平面上

所以双叶双曲面。

（五）椭圆抛物面

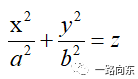
（1）过原点，延z轴正方向是一个逐渐变大的椭圆

（2）切x=0或y=0都是过原点的正向抛物线

所以椭圆抛物面。

（六）双曲抛物面

（1）过原点，延z轴正方向是一个双曲线

（2）切x=0，是一条延z轴负方向的抛物线

（3）切y=0，是一条延z轴正方向的抛物线

所以双曲抛物面。

（七）椭圆柱面

（1）z轴随意取点（高度随意），x-y平面恒椭圆

所以椭圆柱面。

（八）双曲柱面

（1）z轴随意取点（高度随意），x-y平面标准双曲线方程。

所以双曲柱面。

（九）抛物柱面

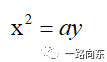
（1）z轴随意取点（高度随意），x-y平面抛物线方程。

所以抛物柱面。

最后给一道题目（源于CMC决赛）

三维空间的直接坐标系中，方程

表示的二次曲面类型是（      ）

解答：

第一步转化：

显然，椭圆柱面。

参考文章：https://zhuanlan.zhihu.com/p/58917013

参考题目：CMC第十二届决赛填空