目录

数制和编码

信息的二进制编码

数值数据的表示

进制计数制

 定点数和浮点数

 定点数的编码表示

原码表示

补码表示

求特殊数的补码

求真值的补码

求补码的真值

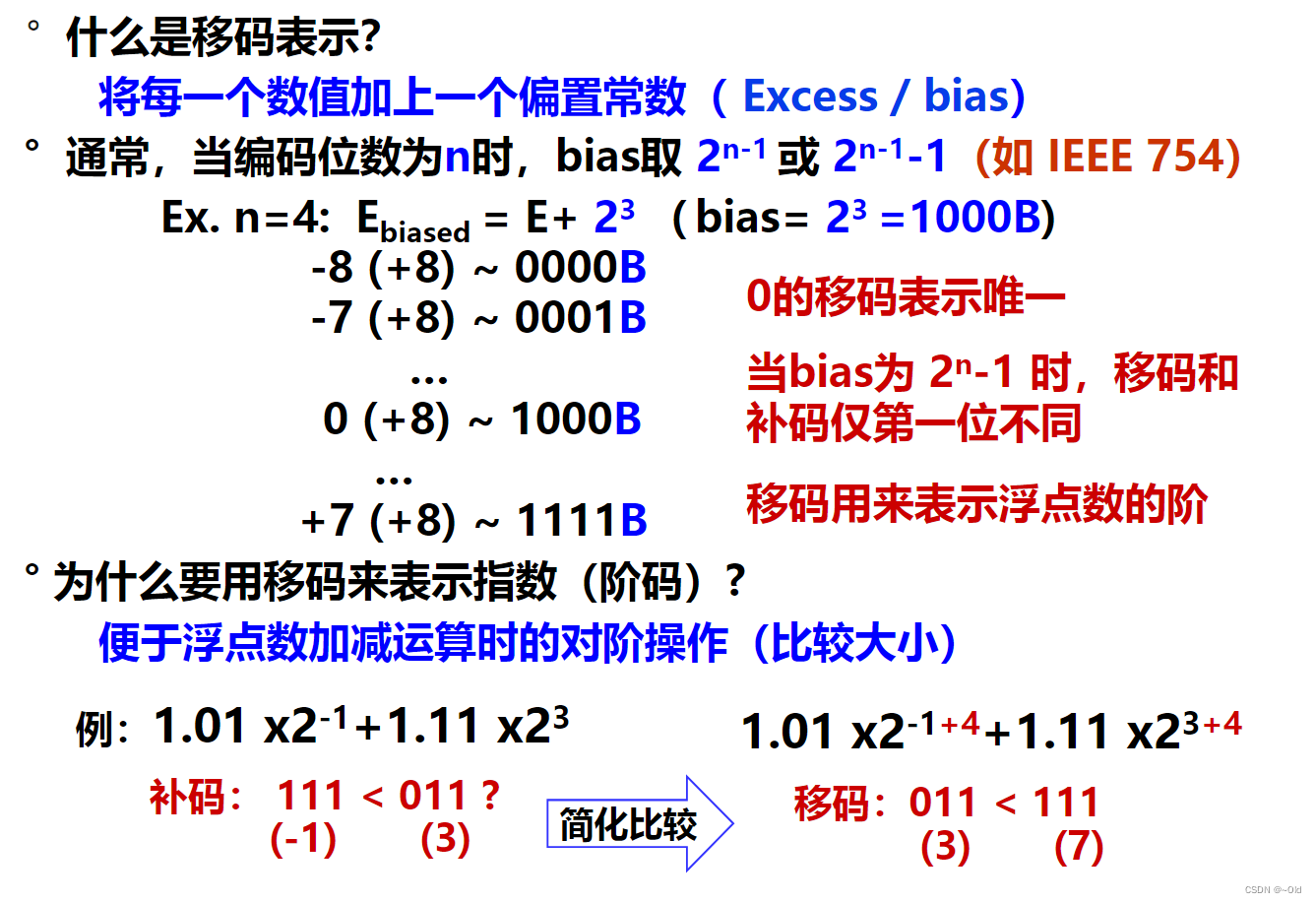
移码表示Excess (biased) notiion

 C语言中的整数

无符号整数(unsigned integer)

带符号整数（Signed integer）

C语言中的整数

个人总结

---

数制和编码

信息的二进制编码

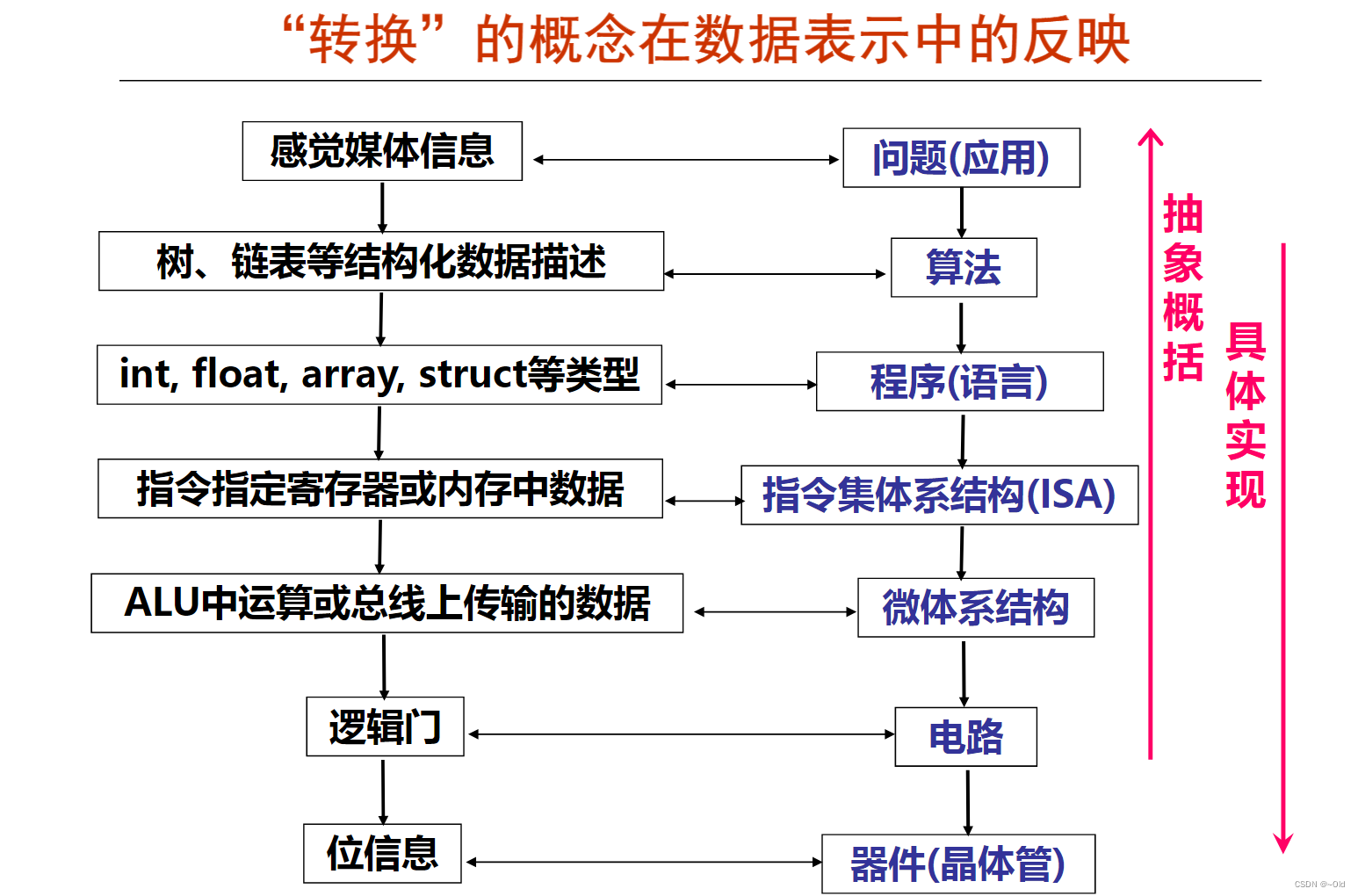
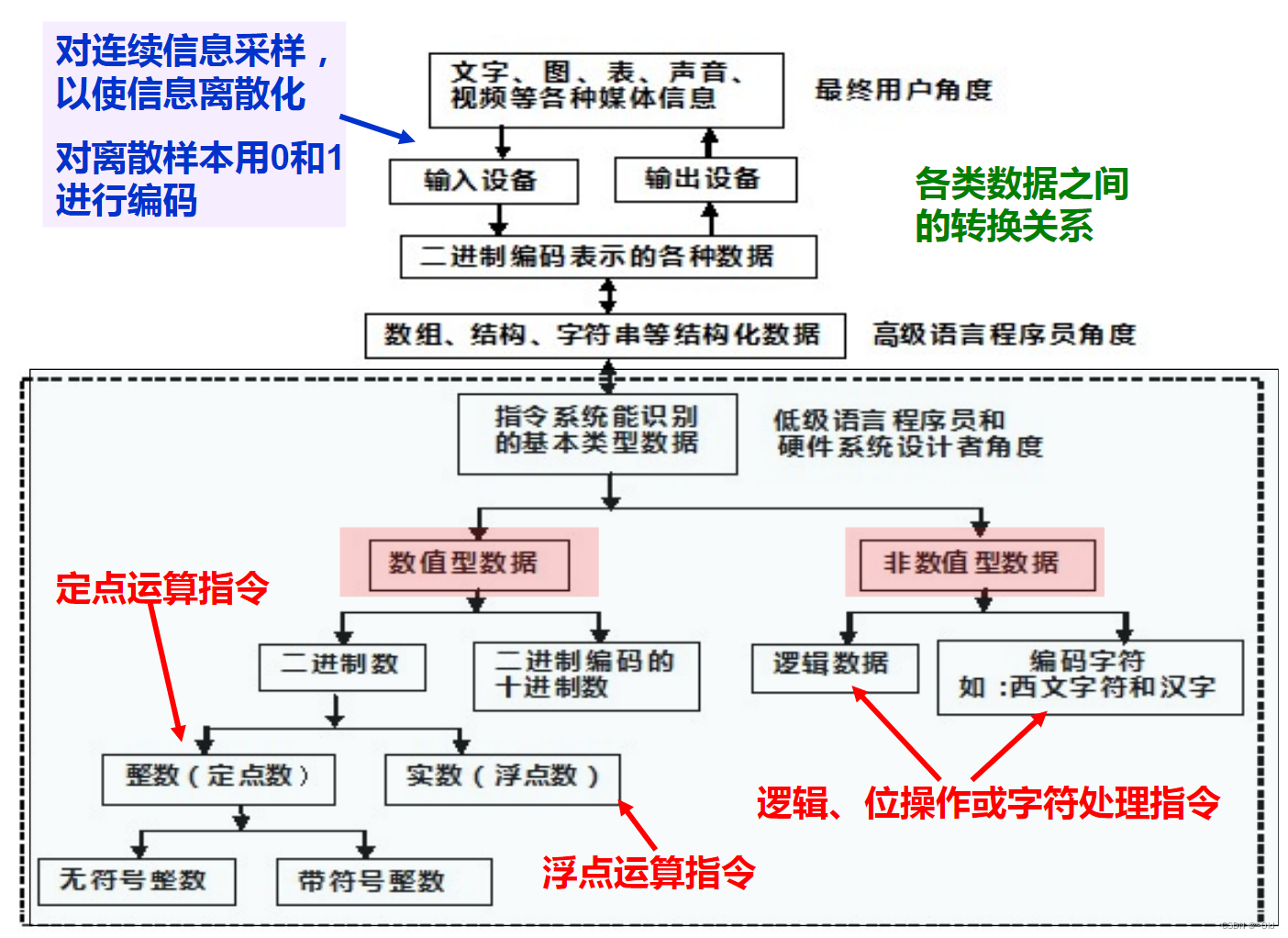
 1、机器级数据分两大类

• 数值数据：无符号整数，带符号整数、浮点数（实数）
• 非数值型数据：逻辑数（包括位串）、西文字符和汉字

2、计算机内部所有信息都用二进制（即：0和1）进行编码

3、用二进制编码的原因

• 制造二个稳态的物理器件容易（电位高/低、脉冲有/无、正/负极）
• 二进制编码、计数、运算规则简单
• 正好与逻辑命题真/假对应，便于逻辑运算
• 可方便的用逻辑电路实现算术运算 

4、真值和机器数

• 机器数：用0和1编码的计算机内部的0/1序列
• 真值：真正的值，即：现实中带正负号的数

例: unsigned short型变量x的真值是127，其机器数是多少 ?127=27-1，其机器数为0000 0000 0111 1111

数值数据的表示

数值数据表示的三要素：进位计数制、定、浮点表示、如何用二进制编码，即要确定一个数值数据的值必须确定这三个要素。

例如：20137564的值是多少？答案是：不知道，因为这个数可以是十进制、也可以是8进制、16进制

1、进位计数制

• 二进制、十进制、八进制、十六进制及其相互转换

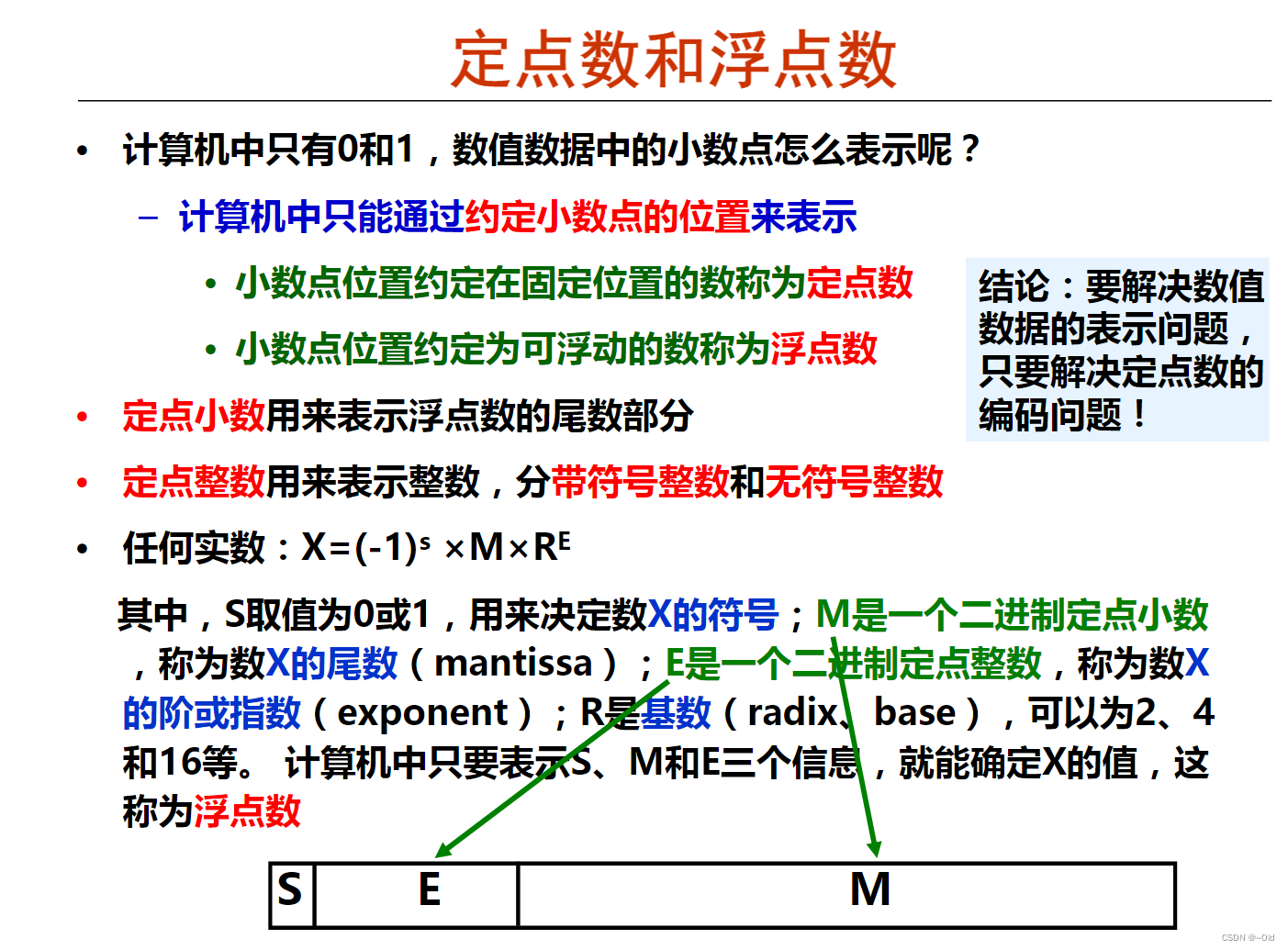
2、定/浮点表示（解决小数点问题，因为机器数中没有小数点的表示）

定点整数、定点小数

浮点数（可以用一个定点小数和一个定点整数表示一个浮点数（科学计数法））

3、定点数的编码（解决正负号的问题）

原码、反码、补码、移码（反码很少用）

进制计数制

（1）R进位计数制

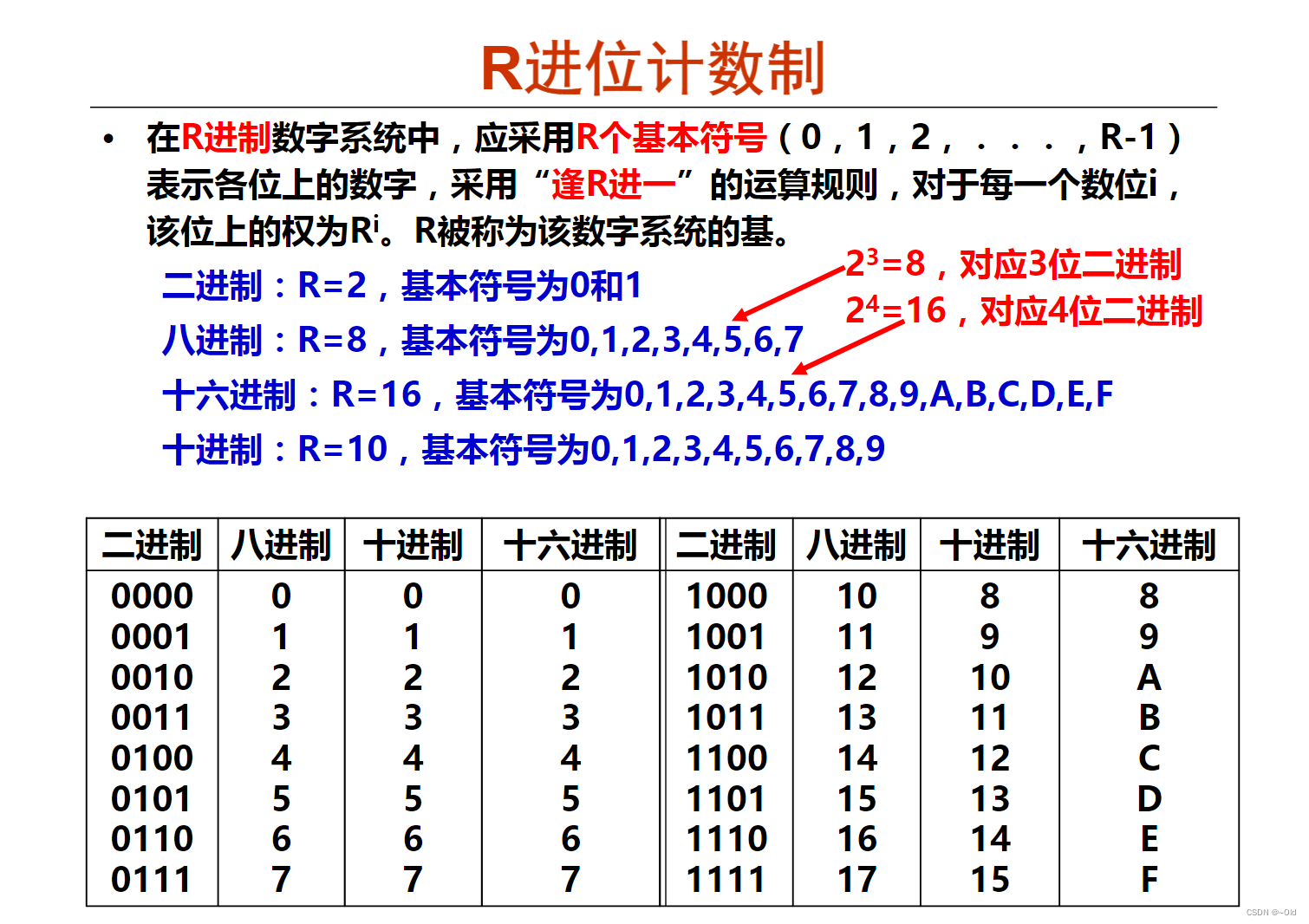
•  八进制/ 十六进制是二进制的简便表示。便于阅读和书写！它们之间对应简单，转换容易。
• 在机器内部用二进制表示，在屏幕或其他设备上表示时，转换为八进制/十六进制数，可缩短长度。

  八进制：Octal （用后缀“O”表示）
  十六进制：Hexadecimal （用后缀“H”，或前缀“0x”表示）

• 现代计算机系统多用十六进制表示机器数

（2）十进制数和R进制数之间的转换

整数——“除基取余，上右下左”    小数——“乘基取整，上左下右”

(3) 十进制数与二进制数之间的转换

整数----“除基取余，上右下左” 小数----“乘基取整，上左下右”
其实，这里就出现了一个问题，小数点在计算机中怎么表示？

(4) 十进制数与八进制数之间的转换

整数----“除基取余，上右下左” 小数----“乘基取整，上左下右”
（可能小数部分总得不到0，此时得到一个近似值 ）

上面的数制转换过程中，出现小数时，有时候无法转换为确切的对应的数值，比如二进制乘以小数一直无法得到整数，这说明一个问题：现实中的精确值可能在机器内部无法用0和1精确表示

 定点数和浮点数

 定点数的编码表示

原码表示

正号用0表示，负号用1表示，数值部分不变

Decimal	Binary	Decimal	Binary
0	0000	-0	1000
1	0001	-1	1001
2	0010	-2	1010
3	0011	-3	1011
4	0100	-4	1100
5	0101	-5	1101
6	0110	-6	1110
7	0111	-7	1111

容易理解，但是：

• 0的表示不唯一，故不利于程序员编程
• 加，减运算方式不统一
• 需额外对符号位进行处理，故不利于硬件设计
• 特别当a<b时，实现a-b比较困难

补码表示

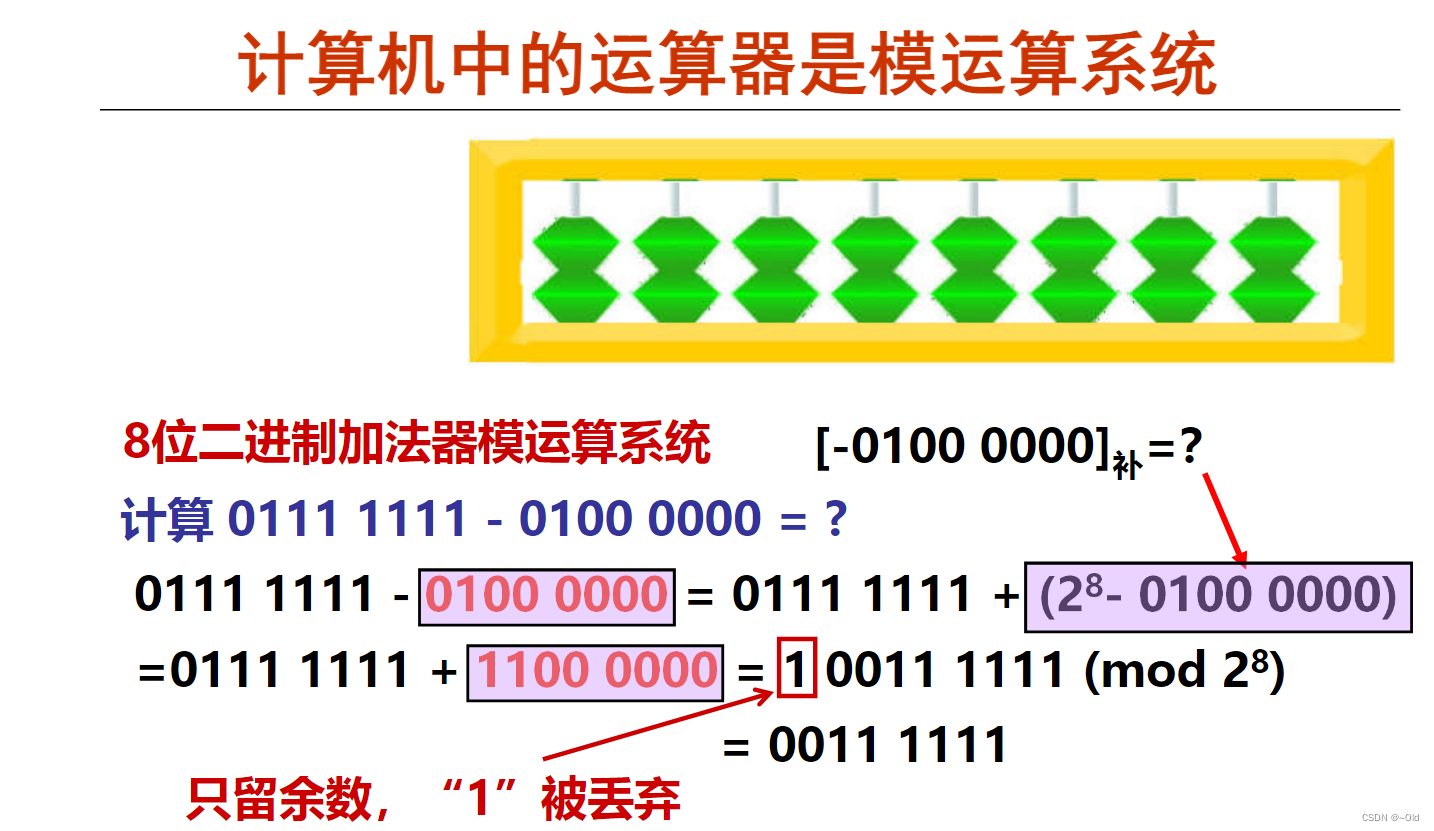
模运算（modular运算）：计算机是一个模运算系统

重要概念：在一个模运算系统中，一个数与它除以“模”后的余数等价

          时钟是一种模12系统 
  假定钟表时针指向10点，要将它拨向6点， 则有两种拨法： 
      ①倒拨4格：10-4 = 6
      ②顺拨8格：10+8 = 18 ≡ 6(mod 12) 
  模12系统中： 10-4 ≡10+8(mod 12)         -4 ≡8(mod 12)    
  则，称8是-4对模12的补码（即：-4的模12补码等于8）。
  同样有-3 ≡9（mod 12） -5 ≡ 7（mod 12）等

结论1：一个负数的补码等于模减该负数的绝对值

结论2：对于某一确定的模，某数减去小于模的另一数，总可以用该数加上另一数负数的补码来代替。（减法统一成加法）

补码的表示

补码（modular运算）：+和-的统一

• 
• 结论1：一个负数的补码等于将对应正数补码，各位取反，末位加1
• 运算器适合用补码表示和运算

        运算器只有有限位，假设为n位，则运算结果只能保留低n位，故可看成是个只有n档的二进制算盘，因此，其模为2^n

        当n=4时，共有16个机器数，0000~1111，可看成是模为2^4的钟表系统。真值的范围为-8~+7

补码的定义：[X]补 = 2^n+X (-2^n<=x<2^n，mod 2^n)，其中X是真值，[x]补是机器数

求特殊数的补码

其中对应于上面的一条结论，一个负数的补码等于模减去该负数的绝对值 

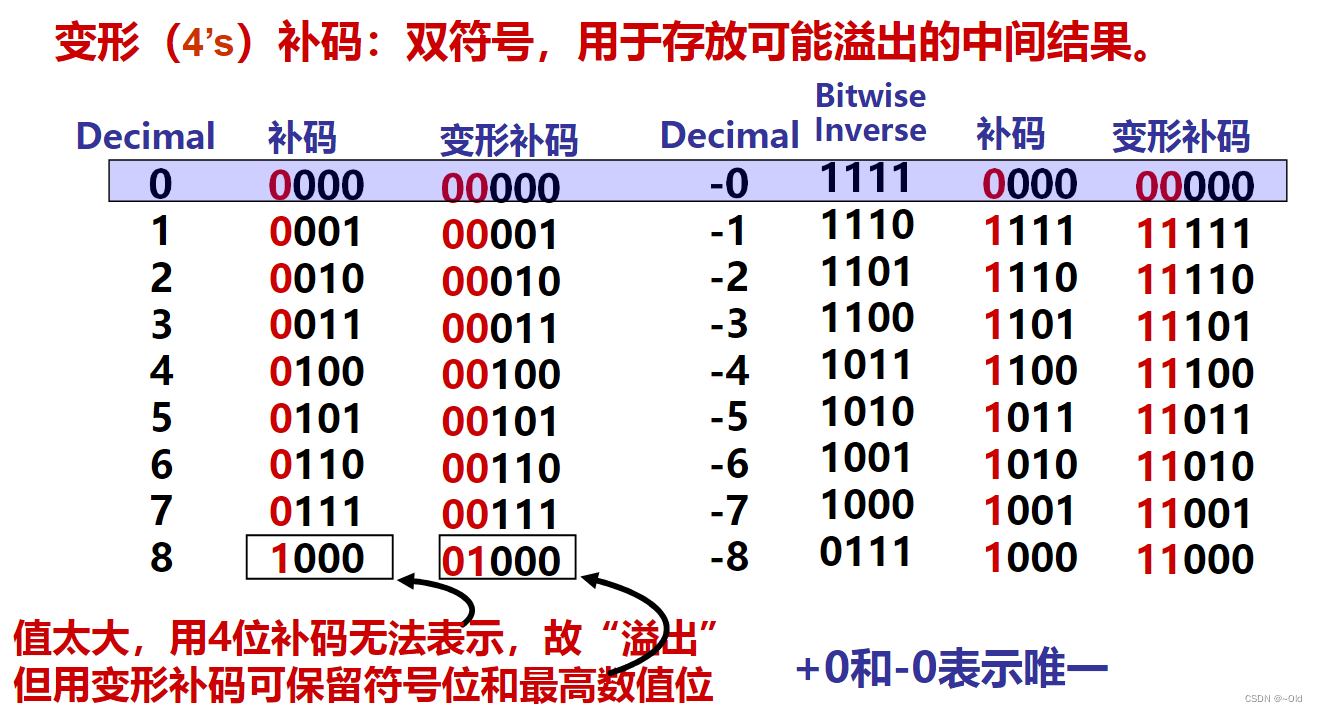
变形补码的表示

补码定义：[X]补 = 2^n+X  (-2^n<=X<2^n, mod 2^n)

• 正数：符号位（sign bit）为0，数值部分不变
• 负数：符号位为1，数值部分，“各位取反，末位加1”
• +0和-0表示唯一

求真值的补码

求补码的真值

移码表示Excess (biased) notiion

 C语言中的整数

无符号整数(unsigned integer)

带符号整数（Signed integer）

 

 其中，多一个最小负数，是因为原码中的+0和-0是不一样的，但是补码是一样的，这里节省下一个表示可以多表示一个1开头的数字，用来表示最小负数

C语言中的整数

无符号数：unsigned int(short/long)；带符号数：int(short/long)常在一个数的后面加一个"u"或“U”表示无符号数

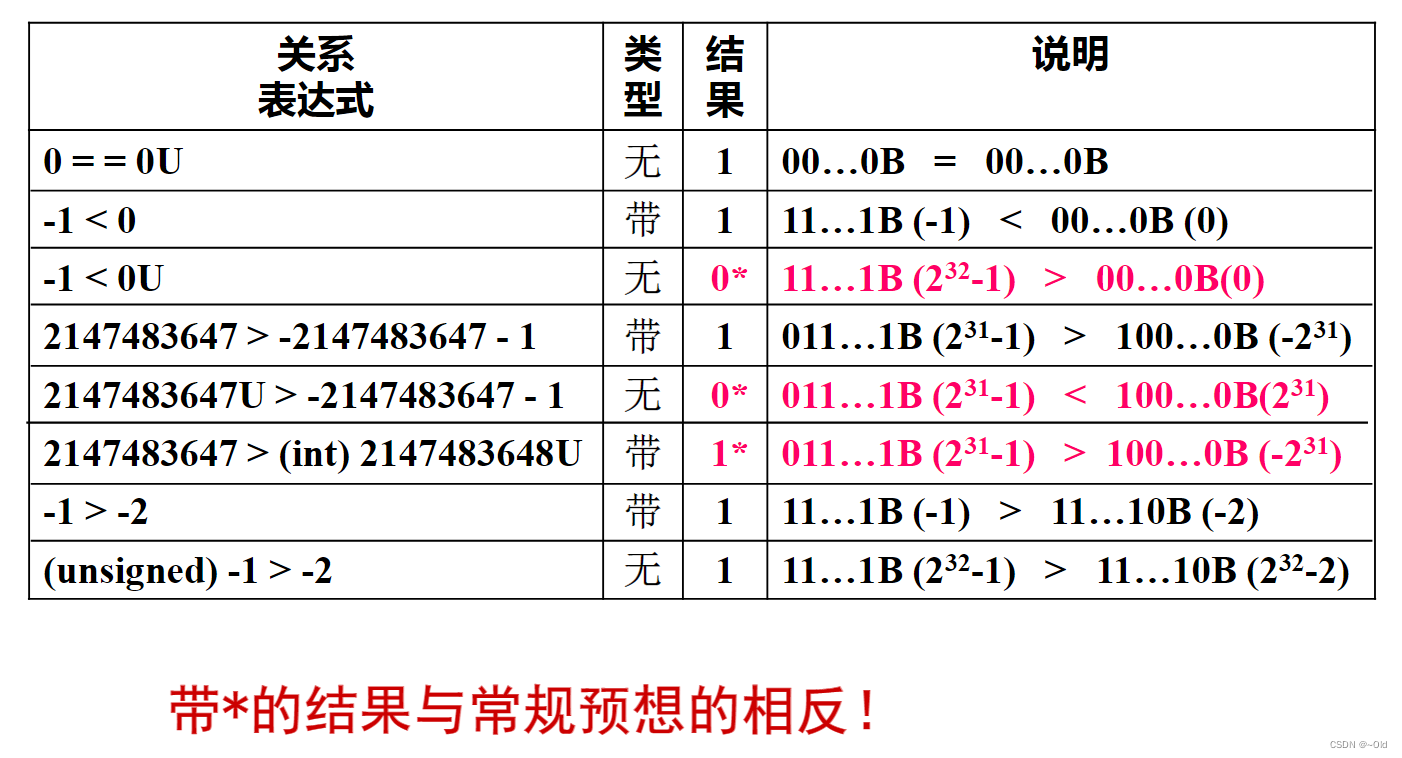
若同时有无符号数和带符号数，则C编译器会将带符号数强制转换为无符号数

例如：

例2：

//考虑以下C代码： 
	int x = –1; 
	unsigned u = 2147483648; 
	printf ( “x = %u = %d\n”, x, x); 
	printf ( “u = %u = %d\n”, u, u); 
//在32位机器上运行上述代码时，它的输出结果:
// x = 4294967295 = –1
// u = 2147483648 = –2147483648 

• 因为-1的补码整数表示为“111...1”，作为32位无符号数解释时，其值为2^32-1 = 4294 967 296 -1=4294967295
• 2^31的无符号数表示为“100...0”，被解释为32位带符号整数，其值为最小负数：-2^(32-1）= -2^31 = -2147483648

编译器处理常量时默认的类型

• C90（C89和C90没什么区别）

范围	类型
0 ~ 2^31-1	int
2^31 ~ 2^32-1	unsigned int
2^32 ~ 2^63-1	long long
2^63 ~ 2^64-1	unsigned long long

• C99

范围	类型
0 ~ 2^31-1	int
2^31 ~ 2^32-1	unsigned int
2^32 ~ 2^63-1	long long
2^63 ~ 2^64-1	unsigned long long

个人总结

Q&A
Q1: 在有些32位系统上，C表达式-2147483648 < 2147483647的执行结 果为false。Why？
A1: 在ISO C90标准下，2147483648为unsigned int型，因此 “-2147483648 < 2147483647”按无符号数比较， 10……0B比01……1B大，结果为false。在ISO C99标准下，“-2147483648 < 2147483647”按带符号整数比较， 10……0B比01……1B小，结果为true。

Q2: 若定义变量“int i=-2147483648;”，则“i < 2147483647”的执行 结果为true。Why？
A2： i < 2147483647 按int型数比较，结果为true。

Q3: 如果将表达式写成“-2147483647-1 < 2147483647”，则结果会怎 样呢？Why？
A3: -2147483647-1 < 2147483647 按int型比较，结果为true。

计算机是一个模运算系统

任何的数在计算机中都是一串01序列，我理解的不同的表示方式比如原码和补码都是机器根据不同的规则进行01序列的解释得到不同的真值，使用补码是为了克服原码带来的种种问题，比如0表示不唯一，+和-运算不统一的问题。

C语言中的常量不同的标准对应的数值范围默认可能是无符号的也可能是带符号的，需根据标准确定，对于带符号表示的时候，比较时，不需要考虑符号位，只要是0符号，就是比1符号位大， 如果符号一样，就考虑后面的二进制序列的大小（负数也一样）。