目录
1. 概述
2. 算法实现
3. 实验结果
总结
Reference
三维点云配准是三维视觉领域一个经典问题,涉及三维重建,定位,SLAM等具体应用问题。传统的配准可以被分为两条技术路线,即基于全局姿态匹配的方法以及基于特征点对应的方法。全局姿态匹配通过在全局范围查找变换矩阵,使得满足预先定义的配准条件,代表方法包括ICP及其变种[1],PointNetLK[2]等。基于特征点对应的方法试图在点云中找到一些具有显著几何特征的keypoints,并按照这些keypoints建立点云之间的对应关系,进而推导出配准结果,代表方法包括FPFH[3],3D SHIFT[4]等。全局方法对点云小范围的缺损不敏感,算法复杂度也相对较低。但是对于局部对全局或局部对局部的配准任务,尤其是低覆盖度点云配准任务,全局方法的性能往往会显著下降。基于特征点对应的方法能够建立针对低覆盖度以及局部对局部的配准算法,但是类似方法对于点云的质量敏感,鲁棒性相对较差。最近,南洋理工大学的研究人员提出一种新的点云配准方法KSS-ICP[5],结合了形状分析与传统ICP算法,有效的改善了配准算法的性能。今天,我在这篇博客里就来介绍一下这篇论文。论文发表于IEEE TIP,链接如下:
arvix:https://arxiv.53yu.com/pdf/2211.02807.pdf
project: GitHub - vvvwo/KSS-ICP
1. 概述
前边已经介绍过了,全局的方法和局部的方法各有优缺点。考虑到目前使用手持扫描设备获取的点云都会携带随机噪声,这使得基于局部几何特征寻找特征点对应的方案不能满足实际需求。因为随机噪声会显著的干扰局部区域的特征提取。因此,针对手持扫描设备获取的点云数据,基于全局方法实现配准,是一个更可行的技术路线。KSS-ICP基于该思路,提供了一个有效的解决方案。
KSS-ICP基于Kendall离散形状空间理论[6],将点云模型进行一种保形的归一化。经过归一化后,点云能够在形状空间中被度量,并通过对度量结果的优化,以获得最优匹配变换,进而退出配准结果。相比传统方法,KSS-ICP的归一化与形状度量有几个好处:1)充分考虑了尺度统一;2)不依赖于点距离;3)对局部区域的噪声鲁棒。KSS-ICP使用中心归一化,将点云视为一组共享源点(中心)的向量组。通过计算向量组的模长,实现尺度统一:
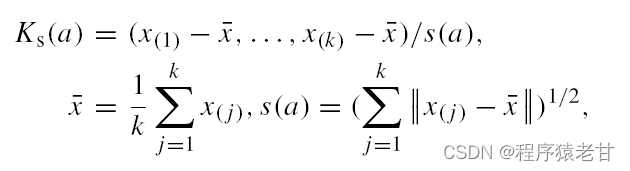
x bar表示的是点云的中心,通过模长计算与归一化,点云a被归一化为Ks(a),实现了对尺度和位移的归一化。通过归一化后,结合形状度量,KSS-ICP能够基于形状相似性建立点云之间的量化分析,该过程不依赖于点距离,因此最大程度避免了局部最优的结果。

基于形状相似性的量化分析,相当于在旋转群SO3中找到一个变换,使得参与度量的两个点云a和b对应一个全度最优的度量结果,即用于配准的变换矩阵。最后,由于形状相似性本身是基于统计形状分析的思想,对于每一个点的随机扰动,其对最终相似性评价的结果影响是相对较小的,因此KSS-ICP的形状度量对噪声是鲁棒的。结合以上三个特点,KSS-ICP给出了一个有效的实现。
2. 算法实现
在介绍算法实现之前,我们需要注意一个小问题。如果我们希望利用概述中所介绍的思路,实现点云配准的话,我们需要首先保证参与配准的点云拥有相同的点数且密度均匀,否则无法实现归一化。因为公式Ks(a)需要计算x bar和进行尺度归一。如果密度不均匀,那么x bar的位置将会有误差;如果点数不相同,那么基于模长实现的尺度归一也会有误差。这里,论文作者引用了自己先前的点云简化工作[7],在实现密度均匀的前提下,保证了点数的统一,如下图所示:
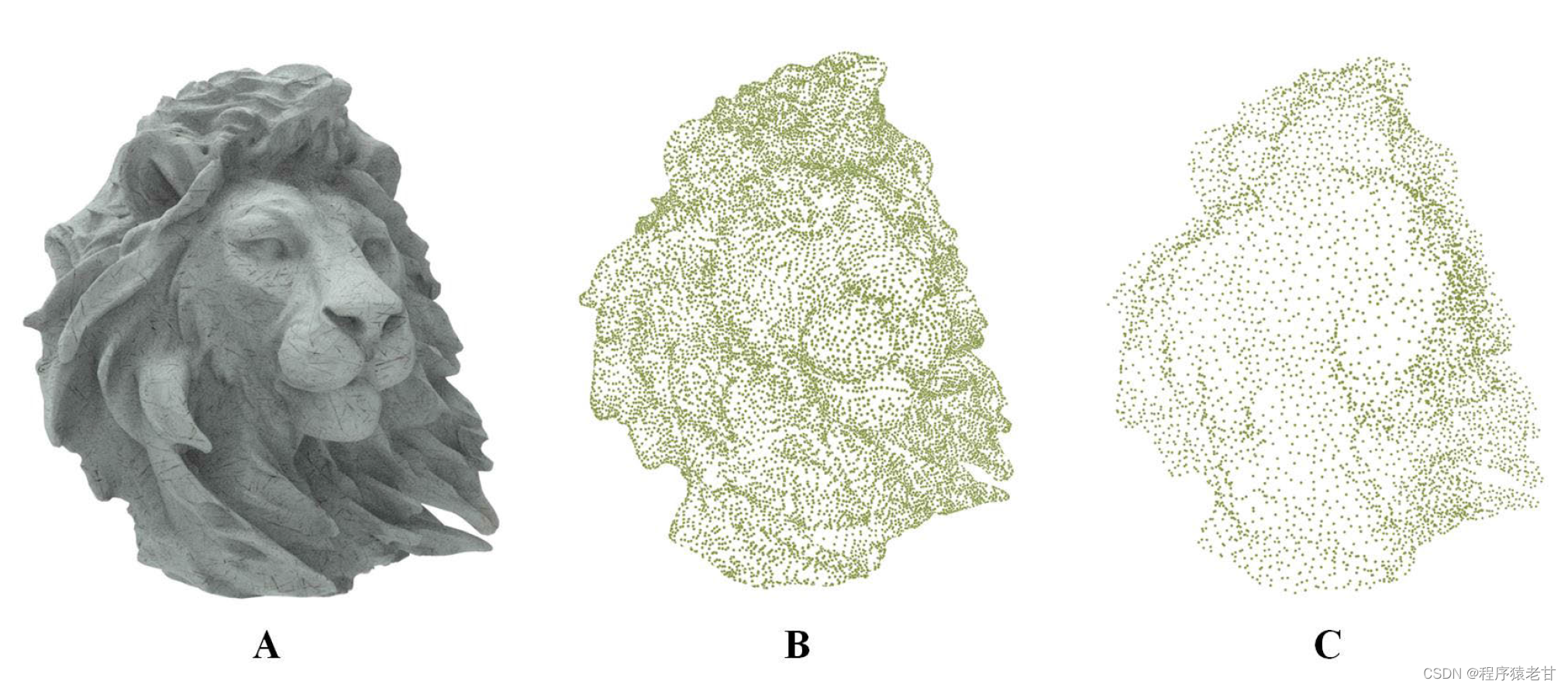
这时,我们就可以利用概述中的方法来进行配准了:

我们针对已经实现归一化的点云,在SO3群中寻找使得形状相似度最小化的变换。这里可以引用一种经典的优化方法来实现,但是作者选择了一个不是很严谨的离散对准方法,即按照旋转方向建立一组离散候选集,然后从候选集中找到最优的结果,最后使用ICP做校正,得到配准结果:
![]()
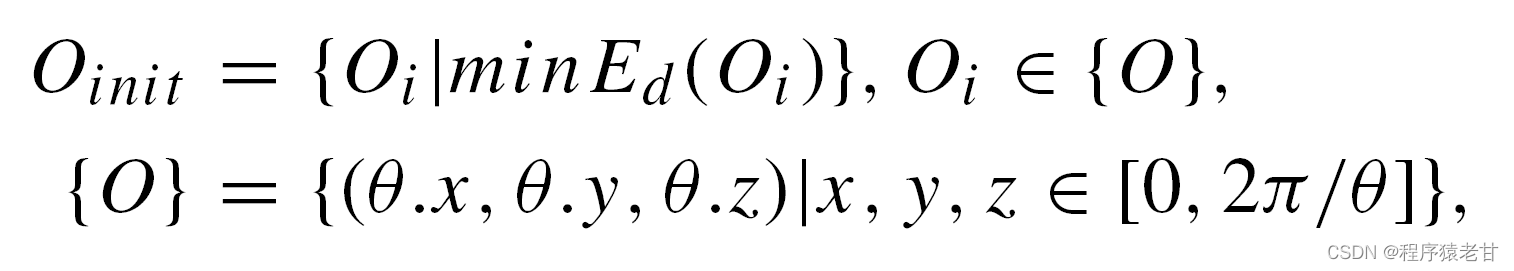
这里作者使用了一个替换函数H,来代替概述中的度量。原因是,原始的形状度量需要点数相同,且一一对应。一一对应显然是不能满足的,因此使用了豪斯多夫距离H来替换形状度量,以描述全局的形状相似性。离散候选集{O}包含了一组旋转变换,KSS-ICP从这样一组旋转变换中找到一个最优结果,然后使用ICP进行二次对齐,进而实现配准的全过程。
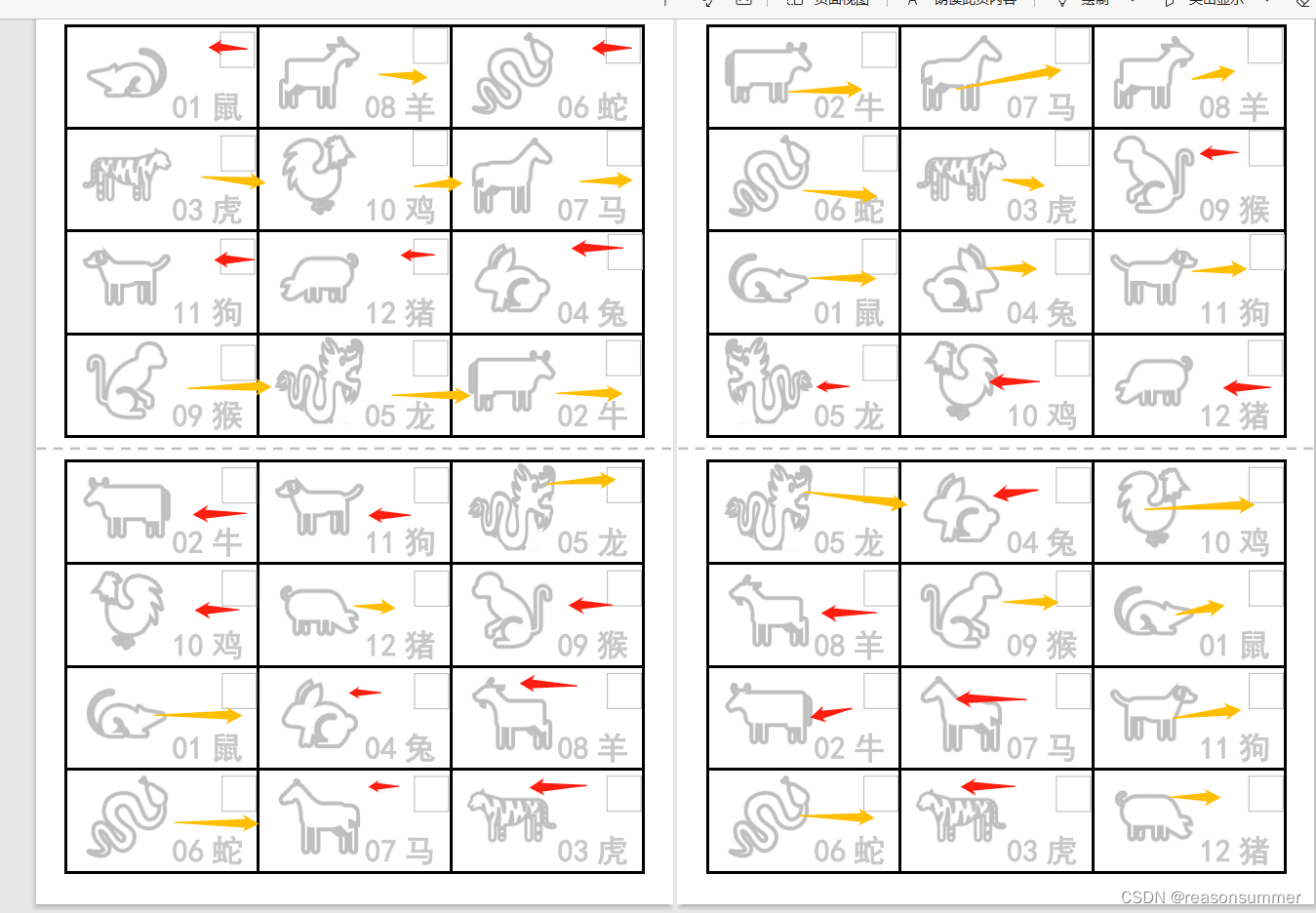
这里有一个显而易见的问题,离散候选集{O}的规模直接决定了算法的精度。对于一些具有对称结构的三维点云,如果离散候选集{O}过小的话,仍然会以很大概率产生局部最优结果。为了弥补该缺陷,作者在配准过程中,加入了一步附加搜索。即第一次的最优结果不是直接输出,而是输出一组结果。这组结果在基于SO3群表示的一个相临区域,能够得到对应的局部最优。作者把所有的局部最优旋转都进行ICP,这样就能进一步降低全局局部最优的概率,如下图所示:
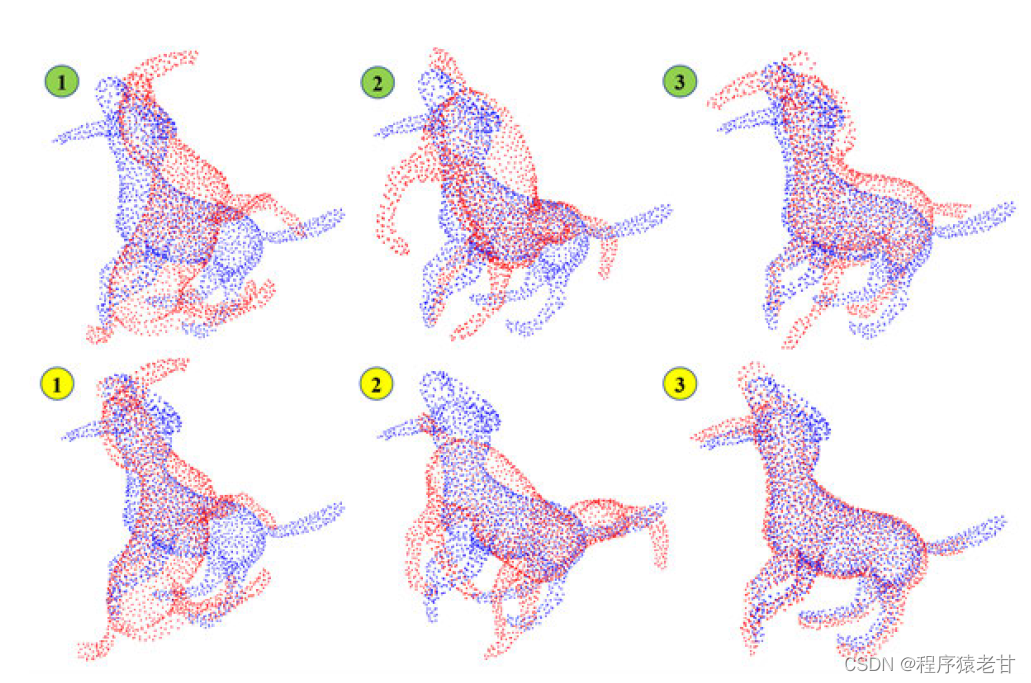
绿色标号的图片表示基于SO3群搜索获取的局部最优结果,黄色表示使用ICP,对局部最优进行二次对准的结果。可以看到,最终我们能够从局部最优结果中选出全局最优解。这个方案在数学上未必严谨,但是在工程上却十分有效,因为点云已经被简化,所有的计算均能使用并行结构进行加速,这就使得整个的查找过程效率很高,且实现了对姿态的全局搜索。
看到这里,细心的朋友一定会提出一个问题,如果是局部对全局的话,那么中心对齐肯定会产生偏差,那么上面的实现就都会失效了,怎么解决这个问题呢?实际上,这里是可以考虑融合局部特征来提供一个解决方案的,但是作者自始至终不想引入局部特征。作者最终给了一个粗暴的解决方案,即引入一些随机的中心候选,在更大的候选集来查找最优匹配:
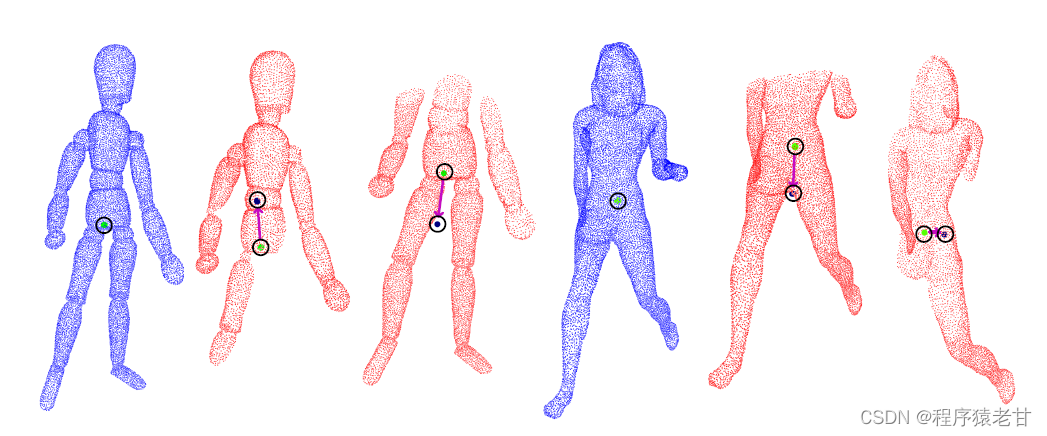
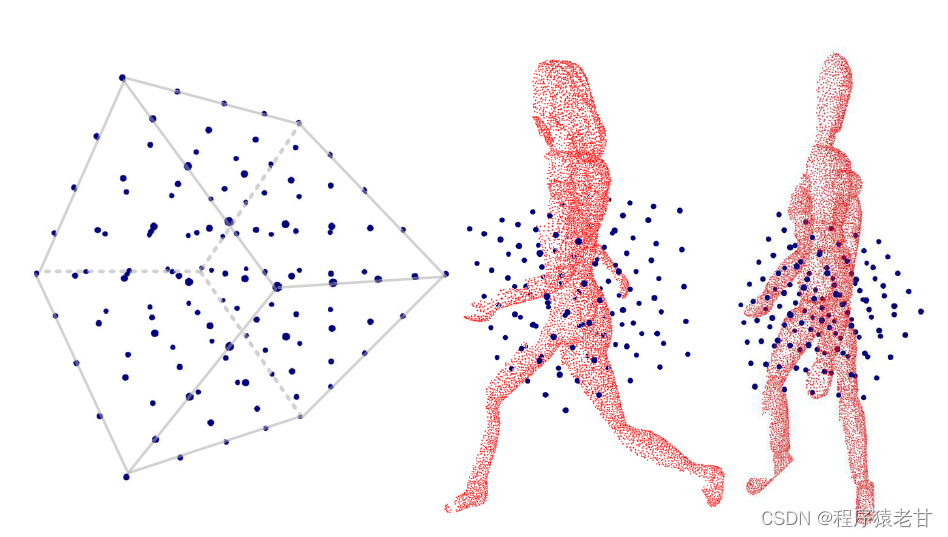
由上图可以看到,点云存在缺失,必然会导致中心的偏移。KSS-ICP在目前查找的中心附近,建立一个中心位移的搜索区域,将所有可能因缺失产生的中心位移全都考虑进去,这样就能在不适用局部特征的前提下,解决中心对齐问题:

上面公式同时考虑了中心位移和旋转两个参数,最终使得KSS-ICP能够在不改变自身基本结构的前提下,实现局部到全局的配准。这样增加了搜索区域,无疑提高了计算量。幸运的是,所有的计算均是离散解耦的,所以可以利用并行结构实现加速:

3. 实验结果
ModelNet40的配准结果:

室内场景RGB3D配准结果:

带有噪声的点云配准结果:
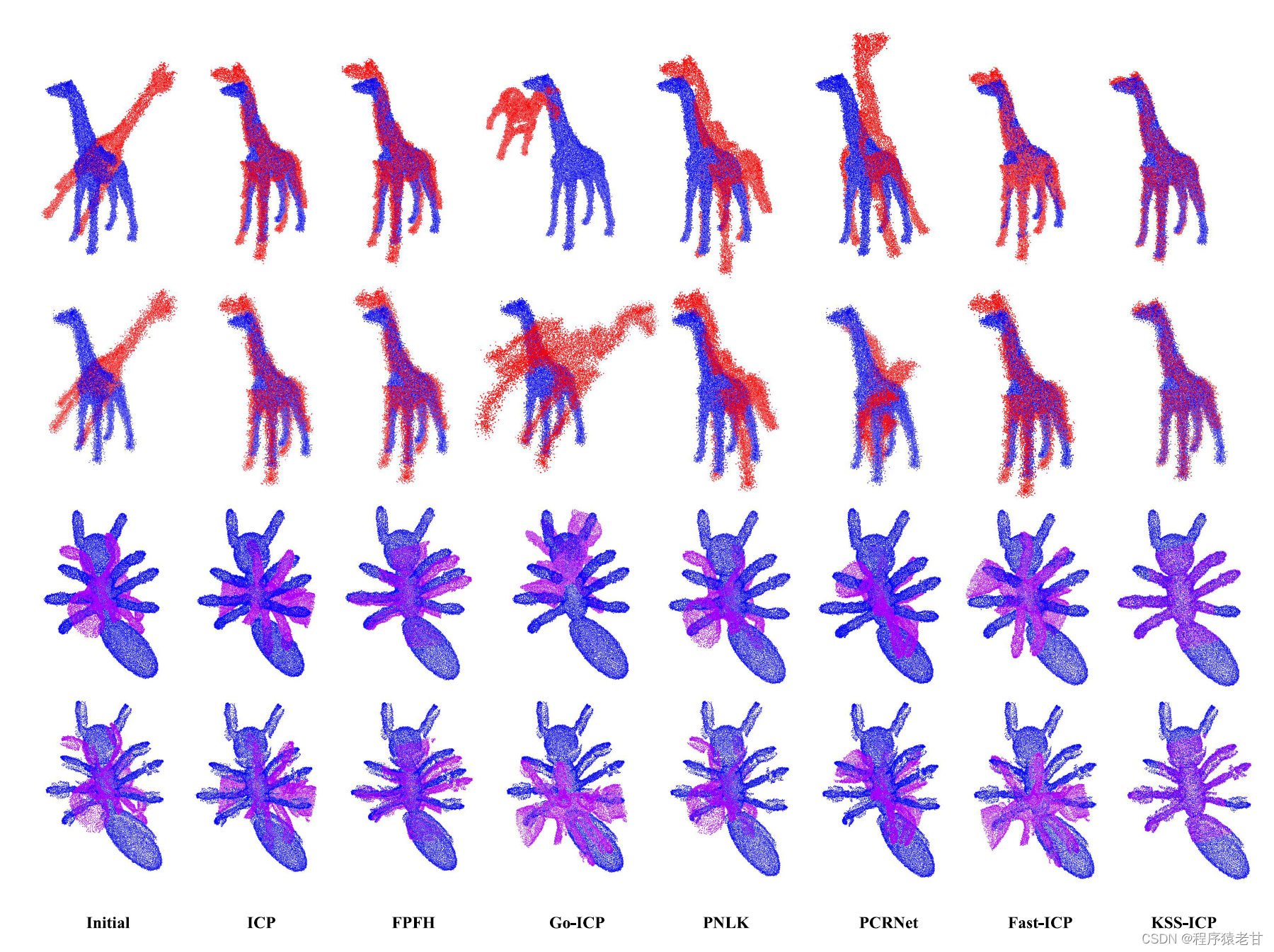
带有缺损区域的点云配准结果:
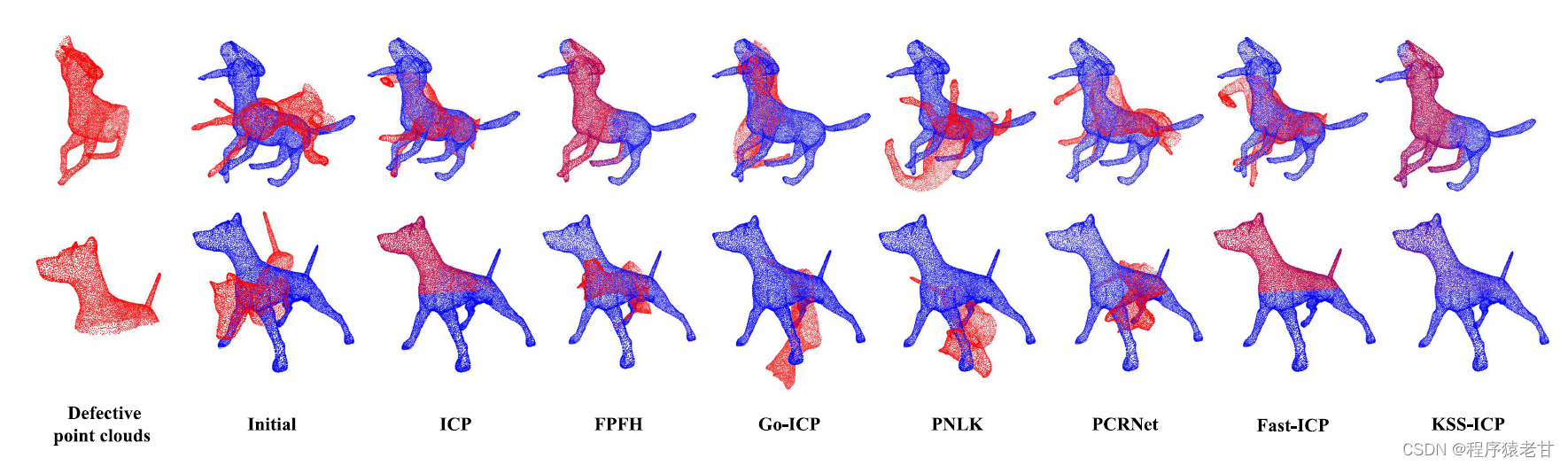
总结
整体来说,KSS-ICP引入了基于流形空间的形状分析工具来建立配准算法的实现,具有一定的启发意义。整个算法的可复现性,鲁棒性,相比于传统方法,均有一定的提升。未来基于该技术路线,有两个可以进一步完善的点:第一,豪斯多夫距离是对形状度量的一种模拟,显然不是评价姿态对应质量的一个很好的选择;第二,为了解决局部到全局的配准,KSS-ICP做了较多的搜索,虽然可以使用并行计算进行加速,但是整个算法的效率还有受到影响。
Reference
[1] J. Yang, H. Li, D. Campbell, et al. Go-ICP: A globally optimal solution to 3D ICP point-set registration[J]. IEEE transactions on pattern analysis and machine intelligence, 2015, 38(11): 2241-2254.
[2] Y. Aoki, H. Goforth, RA. Srivatsan, et al. Pointnetlk: Robust & efficient point cloud registration using pointnet[C]. Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. 2019: 7163-7172.
[3] RB. Rusu, N. Blodow, M. Beetz. Fast point feature histograms (FPFH) for 3D registration[C]. 2009 IEEE international conference on robotics and automation. IEEE, 2009: 3212-3217.
[4] IH. Ferencz, I. Shimshoni. Registration of 3d point clouds using mean shift clustering on rotations and translations[C]. 2017 International Conference on 3D Vision (3DV). IEEE, 2017: 374-382.
[5] C. Lv, W. Lin, B. Zhao. KSS-ICP: Point Cloud Registration based on Kendall Shape Space[J]. IEEE Transactions on Image Processing, 2023.
[6] DG. Kendall. Shape manifolds, procrustean metrics, and complex projective spaces[J]. Bulletin of the London mathematical society, 1984, 16(2): 81-121.
[7] C. Lv, W. Lin, B. Zhao. Approximate intrinsic voxel structure for point cloud simplification[J]. IEEE Transactions on Image Processing, 2021, 30: 7241-7255.