word页码从指定页开始,具体设置步骤
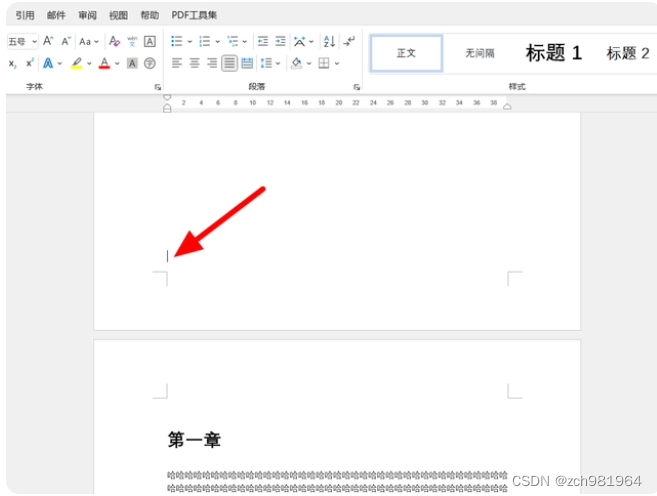
- 1、在文档页面,以目录后第一页为页码开始页为例,也就是正文第一页,首先将鼠标光标定位到目录页最后的位置
- 2、在【布局】选项下点击【分隔符】选项。
- 3、在分隔符中选择【分节符】下的【下一页】。
- 4、完成下一页分节符的插入后文章格式会发生一些变化,文章内容会整体后移。在键盘上按下backspace键,删除换行符让标题重新置顶。
- 5、以在页脚插入页码为例,向下滑动,双击打开要设置为第一页的页脚。
- 6、完成页脚打开,在页眉和页脚菜单下,取消【链接到前一节】选项。
- 7、在页眉和页脚选项下,点击【页码】,出现下拉,点击【设置页码格式】选项。
- 8、在页码格式页面,设置页码的编号格式,起始页码设置为1(默认的起始页码为0),点击【确定】按钮。
- 9、完成页码格式设置,接着要选择插入页码的位置,在【页码】选项下,以页面底端为例,选择要插入页码的位置和样式,以普通数字2为例。
- 10、这样就成功设置页码从指定页开始,双击页眉页脚外的位置,就退出页眉页脚状态成功。
word页码设置从指定页开始,是先添加分节符,然后取消与前一节相同页脚功能,然后添加页码即可从指定页开始。以下为详细步骤:
1、在文档页面,以目录后第一页为页码开始页为例,也就是正文第一页,首先将鼠标光标定位到目录页最后的位置
2、在【布局】选项下点击【分隔符】选项。
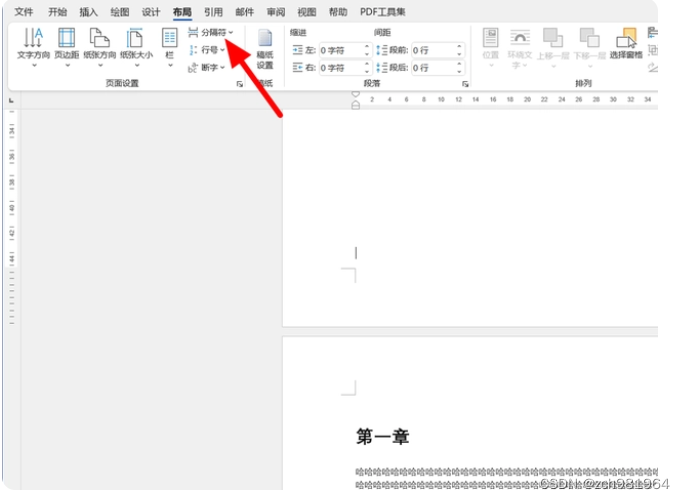
3、在分隔符中选择【分节符】下的【下一页】。
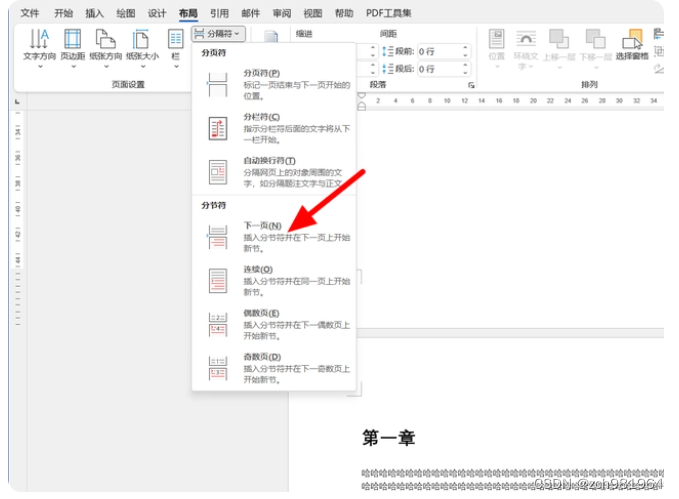
4、完成下一页分节符的插入后文章格式会发生一些变化,文章内容会整体后移。在键盘上按下backspace键,删除换行符让标题重新置顶。
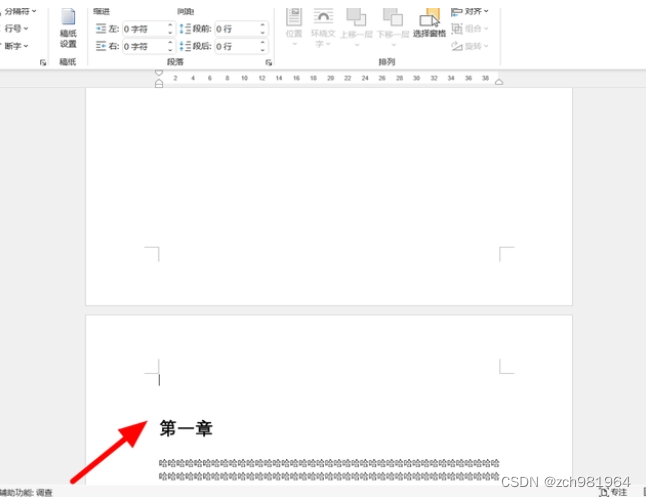
5、以在页脚插入页码为例,向下滑动,双击打开要设置为第一页的页脚。
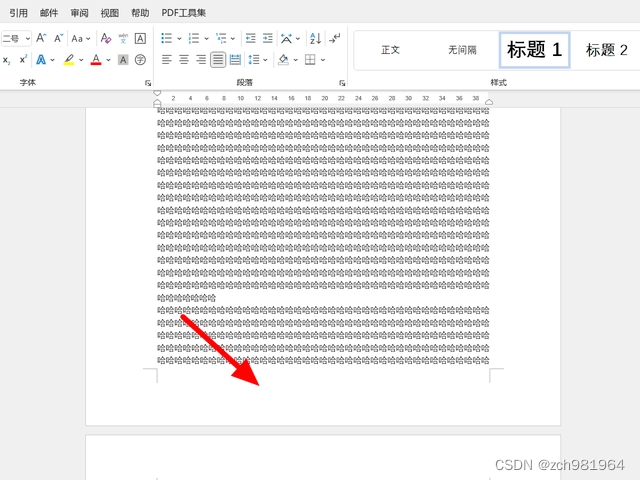
6、完成页脚打开,在页眉和页脚菜单下,取消【链接到前一节】选项。

7、在页眉和页脚选项下,点击【页码】,出现下拉,点击【设置页码格式】选项。
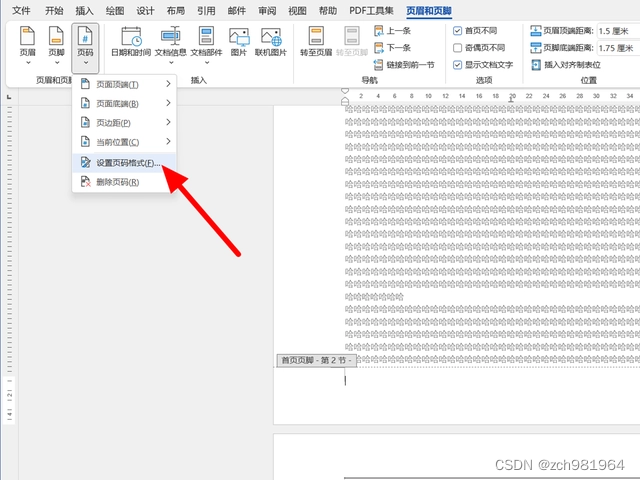
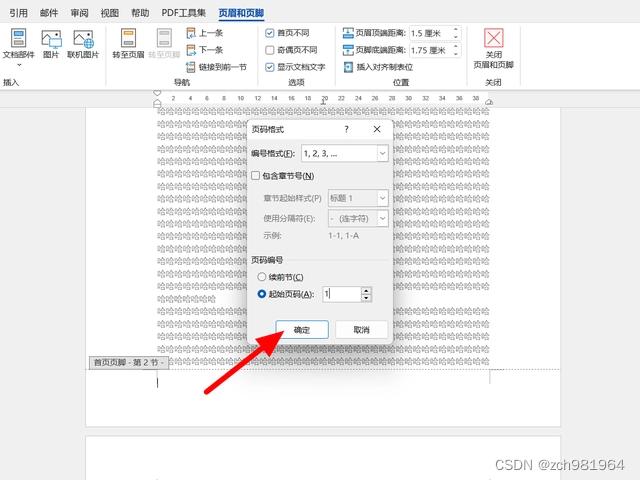
8、在页码格式页面,设置页码的编号格式,起始页码设置为1(默认的起始页码为0),点击【确定】按钮。
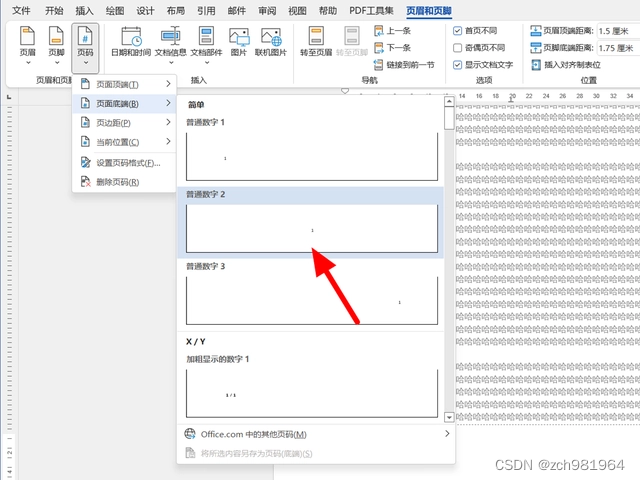
9、完成页码格式设置,接着要选择插入页码的位置,在【页码】选项下,以页面底端为例,选择要插入页码的位置和样式,以普通数字2为例。
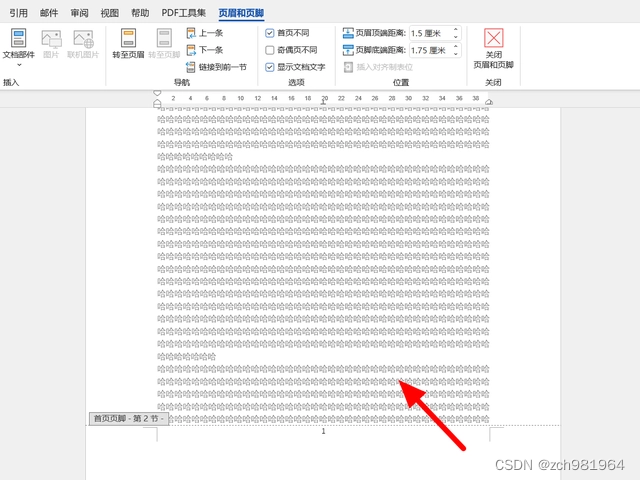
10、这样就成功设置页码从指定页开始,双击页眉页脚外的位置,就退出页眉页脚状态成功。
注意:
1、页码格式和插入页码顺序可以颠倒,只要最终设置好页码是从指定页开始即可。
2、页码想要在那一页开始就打开那一页的页脚即可,操作步骤都是一样的。