提示:时光清浅处 一步一安然
文章目录
- 前言
- 2.3.1 浮点数的表示
- 2.3.2 IEEE754
- 2.2.3 浮点数的运算
前言
本节主要讲三个问题,浮点数的表示,IEEE 754标准,浮点数的加减运算
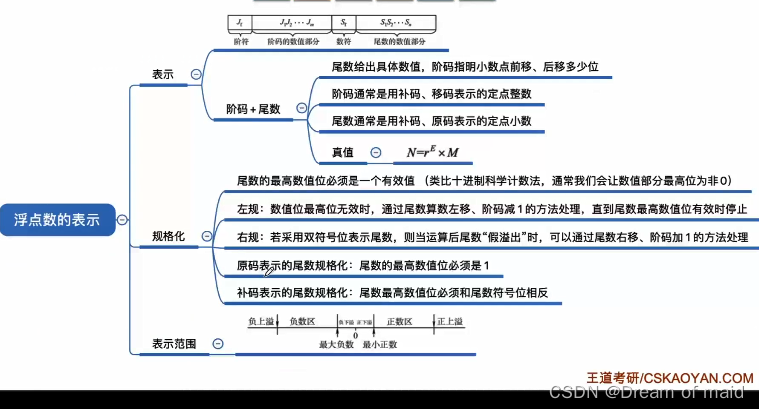
2.3.1 浮点数的表示
浮点数的作用和基本原理
定点数可表示的数字范围有限,但我们不能无限制地增加数据的长度
将一个数值用阶码和尾数来表示,这样表示的数值的范围就大大增加了,

浮点数规格化
尾数的最高位是无效位会丧失精度,规定尾数的最高数值位必须是一个有效值
左规:当浮点数运算的结果为非规格化时要进行规格化处理,讲尾数算数左移一位,阶码减一
右规:当浮点数运算的结果尾数出现溢出,(双符号位为01或10,双符号位中的更高位表示我们当前数值的正负性)时,将尾数算数右移一位,新空出的位置与与双符号位保持一致,这里也就是零,最后阶码加一
采用双符号位,当溢出发生时候,可以挽救,更高的符号位是正确的符号位

浮点数的表示范围
这里要注意用补码表示的负数的尾数,我们为了计算机处理起来方便,我们规定数值位的最高位必须是0,正数依然是1,也就是当符号位为0的时候 数值位为1 当符号位为1的时候数值位为0,如下图右下的例题,我们知道负数的补码是补1的,并且规格化是需最高位为0的,所以也就需要算数左移三位,此时阶码值就要减3

知识点回顾
2.3.2 IEEE754
移码
我们上面说过阶码可以使用移码或者补码来,尾数也可以使用原码或者补码来表示,所以也就需要某些标准,
补码的基础上将符号位取反就能得到移码,注意移码只能用于表示整数
移码的定义:移码=真值+偏置值,此处8位移码的偏置值=128d=1000 0000B 偏置值一般取128D 此时移码=补码符号位取反,IEEEE754取的偏置值127时,此时对于真值-128=1000 0000B 移码=-1000 0000 +0111 1111=1111 1111(这里的计算时是发现被减数比减数要小,由于我们移码只有8bit,所以背后的这些加减运算都会进行mod128,我们可以在原有的基础上加上128,然后再减 此时得到的移码便是1111 1111)
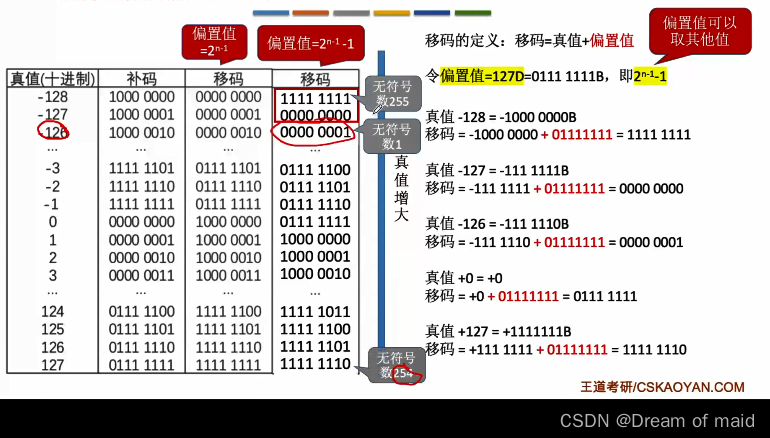
IEEE754
这个表格需要记住,并且在计算时,可以将这个移码看成一个无符号数,然后用之前的计算方式 比如下图double中的蓝色部分的,可以看成无符号数128(移码)-1023(偏移量)
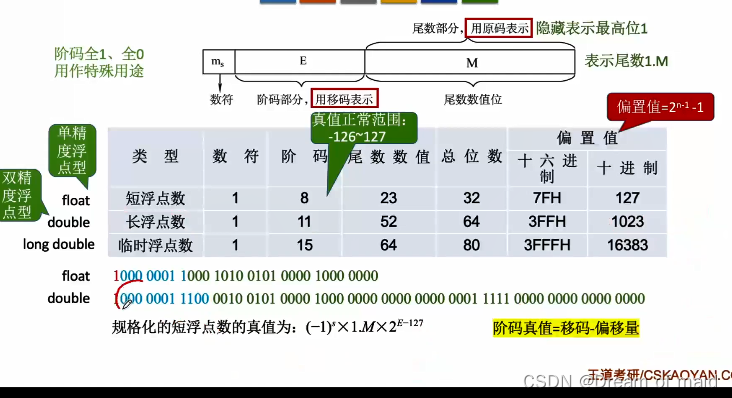


数值范围
之前我们说过-128(全1) -127(全0)有其他用处 所以这里阶码的最小值时-126,所以范围如下
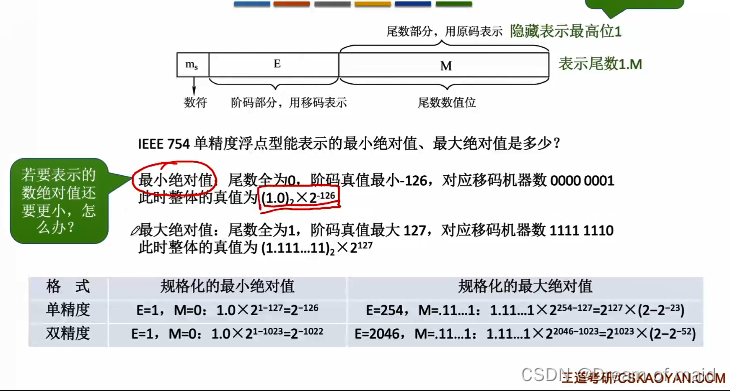
虽然在偏置值为127 时,移码全0 事实上的对应的-127次方,但是这里下图我们会把它固定的视为-126次方,此时是正无穷还是负无穷是看其中的数符位
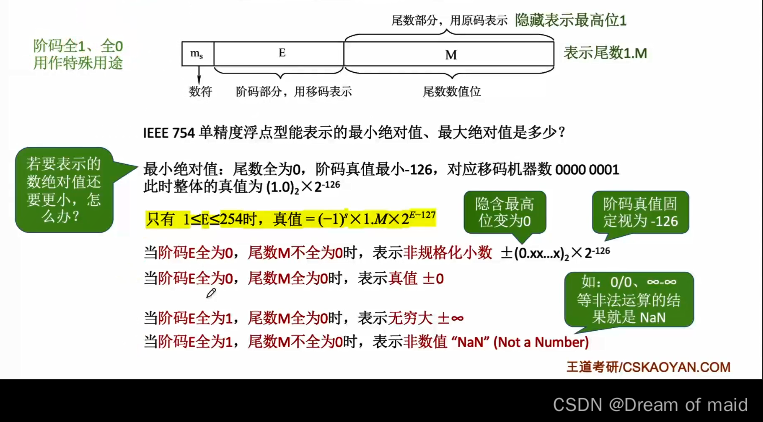
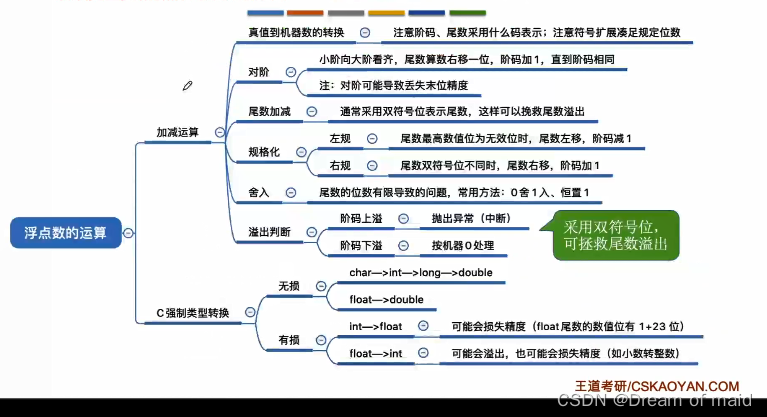
2.2.3 浮点数的运算
本节主要讲的是浮点数的加减法运算,以及强制类型转换
小阶向大阶靠齐是为了计算机内部硬件的实现方便

它的两个符号位是否相同 相同则没有越界,如这里的11 就没有越界
舍入问题
除了右规的时候会面临舍入的问题,有的计算机可能会浮点数的尾数部分单独拆出来计算24bit->32bit 算完结果在经过舍入32bit->24bit再拼回浮点数

本节回顾